2023-2024学年沪科版初中数学八年级下册 19.4 综合与实践 多边形的镶嵌同步分层训练基础题
试卷更新日期：2024-04-02 类型：同步测试
一、选择题
-
1. 用下列一种正多边形瓷砖铺设地面，不能镶嵌整个平面的图形是（ ）A、正六边形 B、正五边形 C、正四边形 D、正三角形2. 有足够多的如下4种边长相等的正多边形瓷砖图案进行平面镶嵌，则不能铺满地面的是（ ）
A、①②④ B、①② C、①④ D、②③3. 如图，张明同学设计了四种正多边形的瓷砖图案，这四种瓷砖图案中，不能铺满地面的是（ ）A、
B、
C、
D、
4. 下列正多边形的地板瓷砖中，单独使用一种不能铺满地面的是（ ）A、正三角形 B、正方形 C、正六边形 D、正八边形5. 如图，将若干个全等的正五边形按图排列组成一个圆圈，图中只排列了前两个正五边形．若要完成这一个圆圈共需要（ ）个这样的正五边形．
A、10 B、9 C、8 D、76. 用正三角形和正六边形镶嵌，若每一个顶点周围有m个正三角形、n 个正六边形，则m，n满足的关系式是( )A、2m+3n=12 B、m+n=8 C、2m+n=6 D、m+2n=67. 四个大小相同的大正方形和一个小正方形的面积之和为260，四个大小相同的长方形的面积之和为64，将它们无缝隙不重叠地摆成图1所示的正方形.现将这四个长方形再次无缝隙不重叠地拼成如图2所示的图形，则该图形的周长为（ ）
A、9 B、18 C、36 D、648. 在下列四种边长均为a的正多边形中，能与边长为a的正三角形作平面镶嵌的正多边形有（ ）①正方形； ②正五边形； ③正六边形； ④正八边形
A、4种 B、3种 C、2种 D、1种二、填空题
-
9. 用等边三角形和正方形作平面镶嵌，则在它的每个顶点周围有个等边三角形和 个正方形．10. 如图，用正多边形镶嵌地面，则图中α的大小为度．
11. 图形的密铺（或称图形的镶嵌）指用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间既不留空隙、也不互相重叠地把一部分平面完全覆盖．图1所示的是一种五边形密铺的结构图，图2是从该密铺图案中抽象出的一个五边形，其中 ， ， 则的度数是 ．
12. 现要用两种不同的正多边形地砖铺地板，若已选用正方形，则还可以选用形与它搭配铺成无空隙且不重叠的地面（只需要写出一种即可）13. 如图，将完全相同的正三角形和完全相同的平行四边形镶嵌成平面图案．则平行四边形中较大的角度数为°．
三、解答题
-
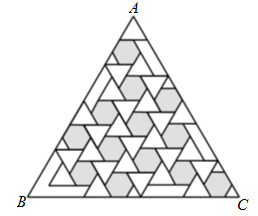
14. 我们学习了平面图形的镶嵌，即用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，就是平面图形的镶嵌．镶嵌平面的图形有很多，值得我们研究的问题也有许多！如图，小亮同学用绘画的方法，设计的一个正三角形的平面镶嵌图，如果整个镶嵌图三角形ABC的面积为75，则图中阴影部分的面积是多少？
15.如何设计计算油漆用量的方案？
素材1
小明家的一面墙壁由边长为1分米的小正方形密铺而成，上面画了如图所示的心形图案.他现在准备将心形图案的内部刷上红色的油漆，已知刷1平方分米需要0.02升的油漆.
素材2
奥地利数学家皮克证明了格点多边形的面积公式，格点多边形的面积S与格点多边形内的格点数a和边界上的格点数b有关，面积公式可表示为（其中m，n为常数）.示例：如图2，格点多边形内的格点数 ， 边界上的格点数 ， 格点多边形的面积.
问题解决
任务1
在图3中画一个格点多边形，并计算它的格点多边形内的格点数a，边界上的格点数b和面积S.
▲
▲
▲
任务2
得出格点多边形的面积公式
根据图2和图3的数据，求常数m，n的值.
任务3
计算油漆的用量
求需要红色油漆多少升？
四、综合题
-
16. 在“平面图形的镶嵌”学习中，主要研究了一种或两种正多边形的镶嵌问题，请运用所学知识完成下列问题．(1)、填写表中空格．
正多边形的边数
6
8
正多边形每个内角的度数
(2)、根据题意，如果仅用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形；(3)、假设在镶嵌的平面图形的一个顶点周围有个正四边形，个正八边形，求和的值，请写出过程．17.(1)、一幅图案，在某个顶点处由三个边长相等的正多边形镶嵌而成．其中的两个分别是正方形和正六边形，则第三个正多边形的边数是 ．(2)、从下列图中选择四个拼图板，可拼成一个矩形，正确的选择方案为 ．（填写拼图板的代码即可）．
(3)、已知：如图， ， ， ． 求证： ．