2023-2024学年沪科版初中数学八年级下册 19.3 矩形 菱形 正方形同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 如图,要使成为菱形,则需添加的一个条件是( )
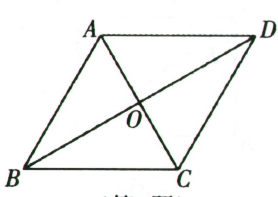 A、 B、 C、 D、2. 如图,已知菱形的边与轴重合,点 , , B(-3,0)若固定点 , , 将菱形沿箭头方向推,当点落在轴上时,点的坐标为( )
A、 B、 C、 D、2. 如图,已知菱形的边与轴重合,点 , , B(-3,0)若固定点 , , 将菱形沿箭头方向推,当点落在轴上时,点的坐标为( )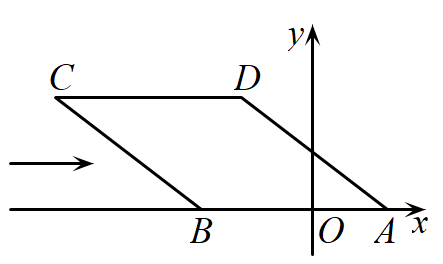 A、 B、 C、 D、3. 如图,菱形花坛的周长为 , , 沿着菱形的对角线修建两条小路和 , 则小路的长是( )
A、 B、 C、 D、3. 如图,菱形花坛的周长为 , , 沿着菱形的对角线修建两条小路和 , 则小路的长是( )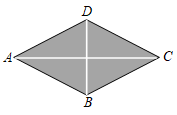 A、 B、 C、 D、4. 如图,在平面直角坐标系xOy中,四边形ABCD是菱形,∠ABC=120°,点B的坐标为(0,﹣2),则菱形ABCD的面积为( )
A、 B、 C、 D、4. 如图,在平面直角坐标系xOy中,四边形ABCD是菱形,∠ABC=120°,点B的坐标为(0,﹣2),则菱形ABCD的面积为( )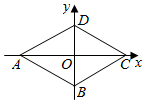 A、16 B、32 C、 D、165. 如图,在矩形中,为边上一点,把沿翻折,使点恰好落在边上的点处, , , 则的长为( )
A、16 B、32 C、 D、165. 如图,在矩形中,为边上一点,把沿翻折,使点恰好落在边上的点处, , , 则的长为( )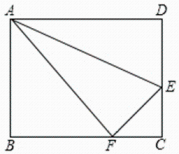 A、 B、 C、 D、6. 如图,在矩形ABCD中,O为AC的中点,过点O作AC的垂线,分别交DC于点F,交AB于点E,G是AE的中点,且∠AOG=30°,有下列结论:①DC=3OG;②OG=BC;③连结AF,CE,四边形AECF为菱形;④其中正确的是( )
A、 B、 C、 D、6. 如图,在矩形ABCD中,O为AC的中点,过点O作AC的垂线,分别交DC于点F,交AB于点E,G是AE的中点,且∠AOG=30°,有下列结论:①DC=3OG;②OG=BC;③连结AF,CE,四边形AECF为菱形;④其中正确的是( ) A、②③ B、③④ C、①②④ D、①③④7. 数学课上,老师让同学们以“矩形的折叠”为主题开展数学活动.如图,小明把矩形沿折叠,使点落在边的点处,其中 , 且 , 则矩形的面积为( )
A、②③ B、③④ C、①②④ D、①③④7. 数学课上,老师让同学们以“矩形的折叠”为主题开展数学活动.如图,小明把矩形沿折叠,使点落在边的点处,其中 , 且 , 则矩形的面积为( ) A、 B、 C、 D、8. 如图,将矩形ABCD沿GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,同时点E,O,F在另一条直线上,小炜同学得出以下结论:①GF∥EC;②AB⑤△COF∽△CEG.其中正确的是( )
A、 B、 C、 D、8. 如图,将矩形ABCD沿GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,同时点E,O,F在另一条直线上,小炜同学得出以下结论:①GF∥EC;②AB⑤△COF∽△CEG.其中正确的是( ) A、①②③ B、①③④ C、①④⑤ D、②③④
A、①②③ B、①③④ C、①④⑤ D、②③④二、填空题
-
9. 已知菱形的对角线的长分别是和 , 则菱形的周长等于 .10. 如图, 中, , , ,D是AB的中点,E是BC的中点, 于点F,则 的长是.
 11. 如图,菱形 ABCD的边长为 2,∠DAB=60°,E为 BC 边的中点,P 为对角线AC 上的一个动点,则 PB+PE的最小值为.
11. 如图,菱形 ABCD的边长为 2,∠DAB=60°,E为 BC 边的中点,P 为对角线AC 上的一个动点,则 PB+PE的最小值为. 12. 如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”如图,已知“完美菱形”的边长为 , 是它的较短对角线,点、分别是边 , 上的两个动点,且满足 , 设的面积为 , 则的取值范围是 .
12. 如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”如图,已知“完美菱形”的边长为 , 是它的较短对角线,点、分别是边 , 上的两个动点,且满足 , 设的面积为 , 则的取值范围是 .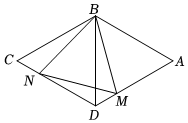 13. 如图,正方形ABCD的周长为80米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按这样的方向每分钟行50米,乙按这样的方向每分钟行40米.如果用记号表示两人行了m分钟,并相遇过n次,那么当两人出发后第一次处在正方形的两个相对顶点位置时,对应的记号应是 .
13. 如图,正方形ABCD的周长为80米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按这样的方向每分钟行50米,乙按这样的方向每分钟行40米.如果用记号表示两人行了m分钟,并相遇过n次,那么当两人出发后第一次处在正方形的两个相对顶点位置时,对应的记号应是 .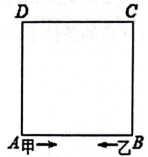
三、解答题
-
14. 如图,直线与坐标轴分别交于点A,B,以OA为边在轴的右侧作正方形AOBC
 (1)、求点A,B的坐标;(2)、如图,点D是x轴上一动点,点E在AD的右侧,.
(1)、求点A,B的坐标;(2)、如图,点D是x轴上一动点,点E在AD的右侧,.①探究发现,点在一条定直线上,请直接写出该直线的解析式
②若点是线段OB的中点,另一动点在直线BE上,且 , 请求出点的坐标.
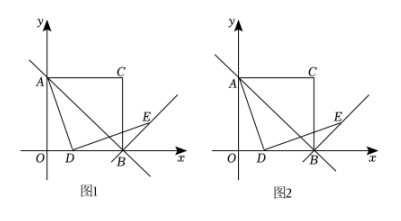
15. 如图1,已知O是坐标原点,点A的坐标是(5,0),B是y轴正半轴上一动点,以OB,OA为边作矩形OBCA,点E,H分别在边BC和OA上,将△BOE沿着OE对折,使点B落在OC上的点F处,将△ACH沿着CH对折,使点A落在OC上的点G处. (1)、求证:四边形OECH是平行四边形.(2)、如图2,当点F,G重合时,求点B的坐标.判断四边形OECH的形状,并说明理由.(3)、当点F,G将对角线OC三等分时,求点B的坐标.
(1)、求证:四边形OECH是平行四边形.(2)、如图2,当点F,G重合时,求点B的坐标.判断四边形OECH的形状,并说明理由.(3)、当点F,G将对角线OC三等分时,求点B的坐标.四、综合题
-
16. 如图,直线与坐标轴分别交于点 , , 以为边在轴的右侧作正方形 .
 (1)、求点 , 的坐标;(2)、如图,点是轴上一动点,点在的右侧, , .
(1)、求点 , 的坐标;(2)、如图,点是轴上一动点,点在的右侧, , .
探究发现,点在一条定直线上,请直接写出该直线的解析式_▲_ ;
若点是线段的中点,另一动点在直线上,且 , 请求出点的坐标.17. 矩形AOBC在平面直角坐标系中的位置如图所示,点A在x轴的负半轴上,点B在y轴的正半轴上,连接AB , 将△ABC沿AB折叠得△ABE , AE交y轴于点D , 线段OD、OA的长是方程x2-7x+12=0的两个根,且OA>OD.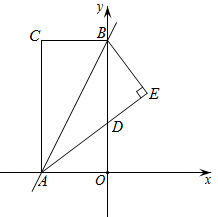 (1)、请直接写出点A的坐标为 , 点D的坐标为;(2)、点P为直线AB上一点,连接PO、PD , 当△POD的周长最小时,求点P的坐标;(3)、点M在x轴上,点N在直线AB上,坐标平面内是否在点Q , 使以B、M、N、Q为顶点的四边形为正方形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
(1)、请直接写出点A的坐标为 , 点D的坐标为;(2)、点P为直线AB上一点,连接PO、PD , 当△POD的周长最小时,求点P的坐标;(3)、点M在x轴上,点N在直线AB上,坐标平面内是否在点Q , 使以B、M、N、Q为顶点的四边形为正方形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.