2023-2024学年沪科版初中数学八年级下册 19.2 平行四边形同步分层训练培优题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，将平行四边形 $A B C D$ 沿对角线 $A C$ 折叠，使点 $B$ 落在点 $B'$ 处，若 $∠ 1 = ∠ 2 = 36 °$ ， $∠ B$ 为（）

A、 $36 °$ B、 $144 °$ C、 $108 °$ D、 $126 °$

查看试题解析
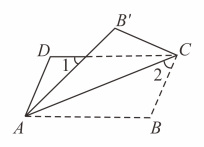2. 下列命题是真命题的是（）

A、若a＞b ，则1－2a＞1－2b B、等腰三角形的角平分线、中线和高重合 C、一组对边平行，另一组对边相等的四边形是平行四边形 D、一个正多边形的内角和为720°，则这个正多边形的一个外角等于60°

查看试题解析
3. 在平行四边形ABCD中，∠BAD的平分线交BC于点E ，若AD=5，BE∶CE=3∶2，则四边形ABCD的周长是 (　　)

A、16　　　　 B、14　　　　 C、12　　　　 D、10

查看试题解析
4. 如图，E ， F分别是▱ABCD的边AD、BC上的点，EF=6，∠DEF=60° ，将四边形EFCD沿EF翻折，得到四边形EFC'D' ， ED'交BC于点G ，则△GEF的周长为 (　　)

A、6　　　　 B、12　　　　 C、18　　　　 D、24

查看试题解析
5. 如图，在 $□ A B C D$ 中，BE平分∠ABC交DC于点E ．若 $∠ A = 60 °$ ，则∠DEB的大小为（）

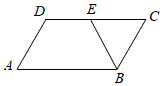A、130° B、125° C、120° D、115°

查看试题解析
6. 如图，在 $△ A B C$ 中，点D ， E ， F分别是 $A B$ ， $B C$ ， $A C$ 中点，以这些点为顶点，在图中能画出多少个平行四边形（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，在平面直角坐标系中，▱OABC的顶点A，C分别在直线x=1和x=4上，O是坐标原点，则对角线OB长的最小值为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $∠ A C B = 45 °$ ， $A B = 2 \sqrt{2}$ ，点 $P$ 为 $B C$ 上任意一点，连结 $P A$ ，以 $P A$ ， $P C$ 为邻边作平行四边形 $P A Q C$ ，连结 $P Q$ ，则 $P Q$ 的最小值为（）

A、 $\sqrt{2}$ B、2 C、 $2 \sqrt{2}$ D、4

查看试题解析

二、填空题

9. 如图，在▱ABCD中，BC的长为4，∠ABC的平分线交AD 于点E，且 E恰好是AD 的中点，过点A作AG⊥BE，垂足为G.若AG=1，则BE的长为.

查看试题解析
10. 如图，在▱ABCD中，∠ABD=25°，现将▱ABCD 折叠成如图所示的形状，使点B与点D 重合，EF 为折痕，点C的对应点为C′，则∠C'EF 的度数为

查看试题解析
11. 如图，在平行四边形ABCD中， $A B = 5$ ， $B C = 8$ ，以点C为圆心，以任意长为半径作弧，分别交CB ， CD于点E ， F ，再分别以E ， F为圆心，以大于 $\frac{1}{2} E F$ 的长为半径作弧，两弧在 $∠ B C D$ 内交于点P ，连接CP并延长交AD于点Q ，连接BQ ．若 $B Q = 7$ 时，则 $△ B Q C$ 与 $△ D C Q$ 的周长之差为．

查看试题解析
12. 如图，在▱ABCD中，对角线AC，BD 相交于点O，E，F 分别是边 AD，AB 上的点，连结 OE，OF，EF.若 $A B = 7 ， B C = 5 \sqrt{2} ，$ ∠DAB=45°，则点 C到直线 AB 的距离是， △OEF周长的最小值是.

查看试题解析
13. 如图，将一副三角尺中，含30°角的三角尺（ $△ A B C$ ）的长直角边与含45°角的三角尺（△ACD）的斜边重合，P，Q分别是边AC，BC上的两点，AB与CD交于E，且四边形EPQB是面积为3的平行四边形，则线段DE的长为.

查看试题解析

三、解答题

14. 如图，在 ▱ ABCD中，AF 平分∠BAD，交 BC 于点F，CE平分∠BCD，交 AD于点 E.

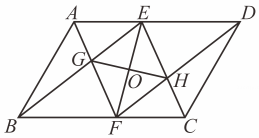(1)、若AD=12，AB=8，求CF 的长.

(2)、连结 BE，与 AF 相交于点 G，连结 DF，与CE 相交于点 H，连结 EF，GH 相交于点O.求证：EF 和GH 互相平分.

查看试题解析
15. 如图： $△ A B C$ 是边长为 $6$ 的等边三角形， $P$ 是 $A C$ 边上一动点．由点 $A$ 向点 $C$ 运动 $(P$ 与点 $A$ ， $C$ 不重合 $)$ ， $Q$ 是 $C B$ 延长线上一点，与点 $P$ 同时以相同的速度由点 $B$ 向 $C B$ 延长线方向运动 $($ 点 $Q$ 不与点 $B$ 重合 $)$ ，过点 $P$ 作 $P E ⊥ A B$ 于点 $E$ ，连接 $P Q$ 交 $A B$ 于点 $D$ ．

(1)、若设 $A P$ 的长为 $x$ ，则 $P C =$ ， $Q C =$ ；

(2)、当 $∠ B Q D = 30 °$ 时，求 $A P$ 的长；

(3)、过点 $Q$ 作 $Q F ⊥ A B$ 交 $A B$ 延长线于点 $F$ ，则 $E P$ ， $F Q$ 有怎样的数量关系？说明理由．

(4)、点 $P$ ， $Q$ 在运动过程中，线段 $E D$ 的长是否发生变化？如果不变，求出线段 $E D$ 的长；如果变化，请说明理由．

查看试题解析

四、综合题

16. 如图，一次函数 $y = k x + b$ 的图象交 $x$ 轴于点 $A$ ， $O A = 4$ ，与正比例函数 $y = - 3 x$ 的图象交于点 $B$ ，点 $B$ 的横坐标为 $- 1$ ．

(1)、求一次函数 $y = k x + b$ 的解析式；

(2)、若点 $C$ 在 $y$ 轴上，且满足 $S_{△ B O C} = \frac{1}{2} S_{△ A O B}$ ，求点 $C$ 的坐标；

(3)、一次函数 $y = k x + b$ 有一点 $D$ ，点 $D$ 的纵坐标为 $1$ ，点 $M$ 为坐标轴上一动点，在函数 $y = - 3 x$ 上确定一点 $N$ ，使得以点 $B$ ， $D$ ， $M$ ， $N$ 为顶点的四边形是平行四边形，写出所有符合条件的点 $N$ 的坐标，并写出求解点 $N$ 的坐标的其中一个情况的过程．

查看试题解析
17. 在平面直角坐标系中，直线 $l_{1}$ ： $y = - \frac{1}{2} x + 6$ 分别与 $x$ 轴， $y$ 轴交于点 $B$ ， $C$ ，且与直线 $l_{2}$ ： $y = \frac{1}{2} x$ 交于点 $A$ ．

(1)、分别求出 $A$ ， $B$ ， $C$ 三点的坐标．

(2)、若 $D$ 是射线 $O A$ 上的点，且 $△ C O D$ 的面积为12，求直线 $C D$ 的函数解析式．

(3)、在（2）的条件下，在平面内是否存在点 $P$ ，使得以 $O$ ， $C$ ， $D$ ， $P$ 为顶点的四边形是平行四边形？若存在，请直接写出点 $P$ 的坐标；若不存在，请说明理由．

查看试题解析