2023-2024学年沪科版初中数学八年级下册 19.1 多边形内角和同步分层训练培优题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

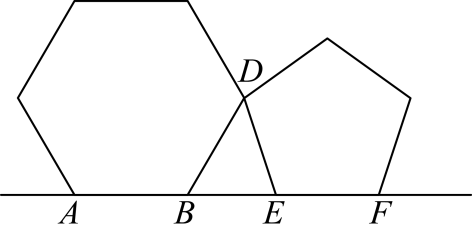
1. 过八边形一个顶点的所有对角线，把这个多边形分成三角形的个数是（）

A、5 B、6 C、7 D、8

查看试题解析
2. 正多边形的每一个外角都是 $30 °$ ，则这个正多边形的内角和是（）

A、 $1080 °$ B、 $720 °$ C、 $360 °$ D、 $1800 °$

查看试题解析
3. 将正六边形与正五边形按如图所示的方式摆放，公共顶点为D ，且正六边形的边 $A B$ 与正五边形的边 $E F$ 在同一条直线上，则 $∠ B D E$ 的度数是（）

A、 $48 °$ B、 $54 °$ C、 $62 °$ D、 $72 °$

查看试题解析
4. 已知一个多边形的每个外角都等于 $45 °$ ，则从这个多边形的某个顶点画对角线，可以画出几条（）

A、5条 B、6条 C、7条 D、8条

查看试题解析
5. 从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n的值是（）

A、6 B、7 C、8 D、9

查看试题解析
6. 如图5，已知三角形纸片ABC中， $∠ A = 69 °$ ， $∠ B = 76 °$ ，将纸片的一角折叠，使点C落在 $△ A B C$ 内，若 $∠ 1 = 22 °$ ，则 $∠ 2$ 的度数为（）

A、 $68 °$ B、 $58 °$ C、 $48 °$ D、 $38 °$

查看试题解析
7. 在多边形的一边上任取一点（不是顶点），将这个点与多边形的各顶点连接起来，可以将多边形分割成8个三角形，则该多边形的边数为（）

A、8 B、9 C、10 D、11

查看试题解析
8. 如图，正方形ABCD的边长为6，点E在边CD上，且CD＝3DE.将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG，CF.则下列结论：①△ABG≌△AFG；②∠AGB+∠AED＝135°；③BG＝CG；④S_△_EGC＝S_△_AFE.其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

9. 如图，在四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠CDA.若∠ABC=56°，则∠BFD的度数为°.

查看试题解析
10. 已知一个多边形的内角和为900°，则这个多边形的边数为.

查看试题解析
11. 如图，D是△ABC内一点，连接AD、BD、CD ， P是∠BDC的角平分线的反向延长线上的一点，连接BP ， ∠ABP＝2∠PBD ， △ABC和△ACD的外角平分线相交于点Q ，若∠Q＝45，∠BDC＝4∠ABD ，则∠P的度数为．

查看试题解析
12. 如图， $A B ∥ C D$ ， E、F分别是AB、CD上的点，EH、FH分别是∠AEG和∠CFG的角平分线.若∠G＝110°，则∠H＝°.

查看试题解析
13. 如图，AB⊥BC，AE平分∠BAD交BC于点E，AE⊥DE，∠1+∠2＝90°，M、N分别是BA，CD延长线上的点，∠EAM和∠EDN的平分线交于点F．下列结论：①AB∥CD；②∠AEB+∠ADC＝180°；③DE平分∠ADC；④∠F为定值．其中结论正确的有．

查看试题解析

三、解答题

14. 如图，在 $△ A B C$ 中， $∠ B A C > 90 °$ ， AB的垂直平分线分别交AB，BC于点E，F，AC的垂直平分线分别交AC，BC于点M，N，直线EF，MN交于点P．

(1)、求证：点P在线段BC的垂直平分线上；

(2)、连接AP，求证：AP平分 $∠ F A N$ ；

(3)、设 $∠ F A N = α$ ，其他条件不变时，求 $∠ F P N$ 的度数．（用含 $α$ 的式子表示）

查看试题解析
15. 观察图形，按规律解答，找出 $n$ 边形的对角线的总数．
图形
每个顶点对角线条数（条）
对角线总条数（条）
三角形
0
0
四边形
1
$\frac{1 \times 4}{2} = 2$
五边形
2
$\frac{2 \times 5}{2} = 5$
六边形
3
10边形
……
……
……
$n$ 边形

查看试题解析

四、综合题

16. 已知 $A B / / C D$ ，点M、N分别是AB、CD上的两点，点 $G$ 在AB、CD之间，连接MG、NG．

(1)、如图1，若 $M G ⊥ N G$ ，求 $∠ B M G + ∠ D N G$ 的度数；

(2)、如图2，点 $P$ 是CD下方一点，MG平分 $∠ B M P$ ， $N D$ 平分 $∠ G N P$ ．若 $∠ B M G = 30 °$ ，求 $∠ M G N$ $+ ∠ M P N$ 的度数；

(3)、如图3，点 $E$ 是AB上方一点，连接EM、EN，且GM的延长线MF平分 $∠ A M E$ ， $N E$ 平分 $∠ C N G$ ．若 $∠ A M E = 50 °$ ，则 $2 ∠ M E N + ∠ M G N$ 的度数为．

查看试题解析

17. 某中学七年级数学课外兴趣小组在探究：“

n

边形

(n > 3)

共有多少条对角线”这一问题时，设计了如下表格，

(1)、请在表格中的横线上填上相应的结果：

多边形的边数	$4$	$5$	$6$	$\dots$	$n$
从多边形的一个顶点出发	$1$	$2$	▲	$\dots$	▲
多边形对角线的总条数	$2$	▲	▲	$\dots$	▲

(2)、应用得到的结果解决以下问题：

①求十二边形有多少条对角线？

②过多边形的一个顶点的所有对角线条数与这些对角线分多边形所得的三角形个数的和可能为 $2023$ 吗？若能，请求出这个多边形的边数；若不能，请说明理由．

查看试题解析

图形	每个顶点对角线条数（条）	对角线总条数（条）
三角形	0	0
四边形	1	$\frac{1 \times 4}{2} = 2$
五边形	2	$\frac{2 \times 5}{2} = 5$
六边形	3
10边形
……	……	……
$n$ 边形