2023-2024学年沪科版初中数学八年级下册 18.2 勾股定理的逆定理同步分层训练基础题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 下列各组数,是勾股数的是( )A、1,2,3 B、0.3,0.4,0.5 C、 , , D、7,24,252. 我国是最早了解勾股定理的国家之一,它被记载于我国古代著名的数学著作《周髀算经》中.下列各组数中,是“勾股数”的是( )A、 B、 C、 D、3. 古埃及人曾经用如图所示的方法画直角:用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,这样做的道理是( )
 A、直角三角形两个锐角互余 B、三角形内角和等于180° C、三角形两边之和大于第三边,两边之差小于第三边 D、如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形4. 我国古代数学著作《九章算术》中有这样一道题:“今有户高多于广六尺,两隅相去适一丈,问户高、广各几何?”大意是:“有一扇矩形门的高比宽多6尺,门的对角线长为1丈(1丈=10尺),那么门的高和宽各是多少?”如果设门的宽为x尺,根据题意,则可列方程为( )A、 B、 C、 D、5. 如图所示的“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.该图由四个全等的直角三角形和一个小正方形拼成一个大正方形,设直角三角形较长直角边长为a , 较短直角边长为b . 若ab=10,大正方形面积为25,则小正方形边长为( )
A、直角三角形两个锐角互余 B、三角形内角和等于180° C、三角形两边之和大于第三边,两边之差小于第三边 D、如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形4. 我国古代数学著作《九章算术》中有这样一道题:“今有户高多于广六尺,两隅相去适一丈,问户高、广各几何?”大意是:“有一扇矩形门的高比宽多6尺,门的对角线长为1丈(1丈=10尺),那么门的高和宽各是多少?”如果设门的宽为x尺,根据题意,则可列方程为( )A、 B、 C、 D、5. 如图所示的“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.该图由四个全等的直角三角形和一个小正方形拼成一个大正方形,设直角三角形较长直角边长为a , 较短直角边长为b . 若ab=10,大正方形面积为25,则小正方形边长为( ) A、 B、2 C、 D、36. 如图,一棵大树在一次强台风中于离地面3米处折断倒下,树干顶部落在与树干底部距离4米处,这棵大树在折断前的高度为( )米
A、 B、2 C、 D、36. 如图,一棵大树在一次强台风中于离地面3米处折断倒下,树干顶部落在与树干底部距离4米处,这棵大树在折断前的高度为( )米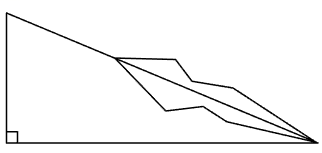 A、5 B、7 C、3 D、87. 如图所示,长为8 cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3 cm至D点,则橡皮筋被拉长了( )
A、5 B、7 C、3 D、87. 如图所示,长为8 cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3 cm至D点,则橡皮筋被拉长了( ) A、2 cm B、3 cm C、4 cm D、5 cm8. 小华新买了一条跳绳,如图1,他按照体育老师教的方法确定适合自己的绳长:一脚踩住绳子的中央,手肘靠近身体,两肘弯屈 , 小臂水平转向两侧,两手将绳拉直,绳长即合适长度。将图1抽象成如图2,若两手握住的绳柄两端距离约为1米,小臂到地面的距离约1. 2米,则适合小华的绳长为( )
A、2 cm B、3 cm C、4 cm D、5 cm8. 小华新买了一条跳绳,如图1,他按照体育老师教的方法确定适合自己的绳长:一脚踩住绳子的中央,手肘靠近身体,两肘弯屈 , 小臂水平转向两侧,两手将绳拉直,绳长即合适长度。将图1抽象成如图2,若两手握住的绳柄两端距离约为1米,小臂到地面的距离约1. 2米,则适合小华的绳长为( ) A、2. 2米 B、2. 4米 C、2. 6米 D、2. 8米
A、2. 2米 B、2. 4米 C、2. 6米 D、2. 8米二、填空题
-
9. 如图,在△ABC中,AB=AC=5,观察尺规作图的痕迹,若BE=2,则BC的长是 .
 10. 如图,每个小正方形的边长都相等, , , 是小正方形的顶点,则的度数为 .
10. 如图,每个小正方形的边长都相等, , , 是小正方形的顶点,则的度数为 .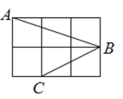 11. 如图,在的网格中,.
11. 如图,在的网格中,. 12. 如图,在的正方形方格图中,小正方形的顶点称为格点,的顶点都在格点上,则是三角形.
12. 如图,在的正方形方格图中,小正方形的顶点称为格点,的顶点都在格点上,则是三角形. 13. 棱长分别为3 cm和2 cm的两个正方体如图所示放置,点A,B,E在同一直线上,顶点G在棱BC上,点P是棱E1F1的中点.一只蚂蚁要沿着正方体的表面从点A爬到点P,它爬行的最短距离是.
13. 棱长分别为3 cm和2 cm的两个正方体如图所示放置,点A,B,E在同一直线上,顶点G在棱BC上,点P是棱E1F1的中点.一只蚂蚁要沿着正方体的表面从点A爬到点P,它爬行的最短距离是.
三、解答题
-
14. 如图,某住宅小区在施工过程中留下了一块空地,已知米,米, , 米,米.
 (1)、求这块空地的面积.(2)、若每种植1平方米草皮需要200元,问总共需投入多少元?15. 高州市在创建“全国文明城市”期间,某小区在临街的拐角清理出了一块可以绿化的空地.如图,经技术人员的测量,已知AB=9m , BC=12m , CD=17m , AD=8m , ∠ABC=90°.
(1)、求这块空地的面积.(2)、若每种植1平方米草皮需要200元,问总共需投入多少元?15. 高州市在创建“全国文明城市”期间,某小区在临街的拐角清理出了一块可以绿化的空地.如图,经技术人员的测量,已知AB=9m , BC=12m , CD=17m , AD=8m , ∠ABC=90°. (1)、求空地的面积;(2)、若平均每平方米空地的绿化费用为150元,试计算绿化这片空地共需花费多少元?
(1)、求空地的面积;(2)、若平均每平方米空地的绿化费用为150元,试计算绿化这片空地共需花费多少元?四、综合题