沪科版初中数学八年级下册 18.1 勾股定理同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 已知如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则EC=( )
 A、3 B、4 C、5 D、62. 已知三角形的两边长分别是8和6,第三边的长是一元二次方程(x-6)(x-10)=0的一个实数根,则该三角形的面积是( )A、24或2 B、24 C、2 D、8或243. 如图,轴、轴上分别有两点、 , 以点为圆心,为半径的弧交轴负半轴于点 , 则点的坐标为( )
A、3 B、4 C、5 D、62. 已知三角形的两边长分别是8和6,第三边的长是一元二次方程(x-6)(x-10)=0的一个实数根,则该三角形的面积是( )A、24或2 B、24 C、2 D、8或243. 如图,轴、轴上分别有两点、 , 以点为圆心,为半径的弧交轴负半轴于点 , 则点的坐标为( )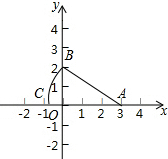 A、 B、 C、 D、4. 如图,在Rt△ABC中,以点A为圆心,适当长为半径作弧,交AB于点F,交AC于点E,分别以点E,F为圆心,大于EF长为半径作弧,两弧在∠BAC的内部相交于点G,作射线AG交BC于点D.若AC=3,BC=4,则CD的长为( )
A、 B、 C、 D、4. 如图,在Rt△ABC中,以点A为圆心,适当长为半径作弧,交AB于点F,交AC于点E,分别以点E,F为圆心,大于EF长为半径作弧,两弧在∠BAC的内部相交于点G,作射线AG交BC于点D.若AC=3,BC=4,则CD的长为( ) A、 B、1 C、 D、25. 将一副直角三角板和一把宽度为2的直尺按如图方式摆放:先把60°和45°角的顶点及它们的直角边重合,再将此直角边垂直于直尺的上沿,重合的顶点落在直尺下沿上.这两个三角板的斜边分别交直尺上沿于A,B两点,则AB的长是( )
A、 B、1 C、 D、25. 将一副直角三角板和一把宽度为2的直尺按如图方式摆放:先把60°和45°角的顶点及它们的直角边重合,再将此直角边垂直于直尺的上沿,重合的顶点落在直尺下沿上.这两个三角板的斜边分别交直尺上沿于A,B两点,则AB的长是( ) A、 B、 C、2 D、6. 如图,在中, , , 以点A为圆心,AC长为半径画弧,交线段AB于点D;以点B为圆心,BD长为半径画弧,交线段BC于点E . 若 , 则AC的长为( )
A、 B、 C、2 D、6. 如图,在中, , , 以点A为圆心,AC长为半径画弧,交线段AB于点D;以点B为圆心,BD长为半径画弧,交线段BC于点E . 若 , 则AC的长为( ) A、12cm B、13cm C、14cm D、15cm7. 如图,在中, , 点D为中点, , 绕点D旋转,分别与边 , 交于E,F两点,下列结论:①;②;③;④始终为等腰直角三角形,其中正确的是( )
A、12cm B、13cm C、14cm D、15cm7. 如图,在中, , 点D为中点, , 绕点D旋转,分别与边 , 交于E,F两点,下列结论:①;②;③;④始终为等腰直角三角形,其中正确的是( ) A、①②④ B、①②③ C、③④ D、①②③④8. 如图,中, , 分别以、、为边在的同侧作正方形、、 , 四块阴影部分的面积分别为、、、.若已知 , 则的值为( )
A、①②④ B、①②③ C、③④ D、①②③④8. 如图,中, , 分别以、、为边在的同侧作正方形、、 , 四块阴影部分的面积分别为、、、.若已知 , 则的值为( ) A、18 B、24 C、25 D、36
A、18 B、24 C、25 D、36二、填空题
-
9. 如图,一架15m长的梯子AB斜靠在一竖直的墙OA上,这时梯子的顶端A离地面距离OA为12m,如果梯子顶端A沿墙下滑3m至C点,那么梯子底端B向外移至D点,则BD的长为m.
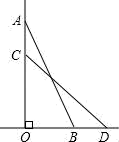 10. 如图,在中, , 以为圆心,CD为半径画弧,交斜边AD于点 , 则下列说法正确的是.(填序号)
10. 如图,在中, , 以为圆心,CD为半径画弧,交斜边AD于点 , 则下列说法正确的是.(填序号)
①是等边三角形,② , ③ , ④
11. 如图,数轴上点A , B分别对应2,4,过点B作 , 以点B为圆心,AB长为半径画弧,交PQ于点C;以原点O为圆心,OC长为半径画弧,交数轴于点M , 则BM的长为 . 12. 如图,在中, , , 点是边上一点(点不与点 , 重合),将沿翻折,点的对应点为点 , 交于点 , 若 , 则点到线段的距离为 .
12. 如图,在中, , , 点是边上一点(点不与点 , 重合),将沿翻折,点的对应点为点 , 交于点 , 若 , 则点到线段的距离为 . 13. 如图,中, , 于点 , 平分 , 交与点 , 于点 , 且交于点 , 若 , , 则 .
13. 如图,中, , 于点 , 平分 , 交与点 , 于点 , 且交于点 , 若 , , 则 .
三、解答题
-
14. 如图1,在中, , , 点D为内部一点, , 连接DC , 将DC绕点D逆时针旋转得到DE , 连接CE交AD于点F , 连接AE , BD .
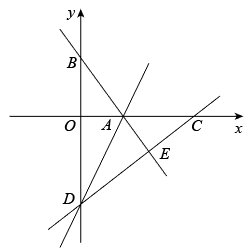
 (1)、求证:;(2)、如图2,当点E落在AB上时,求的度数;(3)、如图3,若F为AD的中点, , 求AD的长.15. 如图所示,在平面直角坐标系xOy中,直线y=-x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)、求证:;(2)、如图2,当点E落在AB上时,求的度数;(3)、如图3,若F为AD的中点, , 求AD的长.15. 如图所示,在平面直角坐标系xOy中,直线y=-x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处. (1)、求AB的长.(2)、求点C和点D的坐标.(3)、y轴上是否存在一点P,使得S△PAB=S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求AB的长.(2)、求点C和点D的坐标.(3)、y轴上是否存在一点P,使得S△PAB=S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.四、综合题