沪科版初中数学八年级下册 18.1 勾股定理同步分层训练基础题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
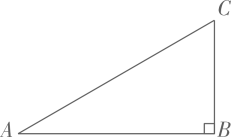
1. 已知直角三角形的两条直角边长恰好是方程的两个根,则此直角三角形斜边长是( )A、13 B、5 C、 D、2. 如图,网格中每个小正方形的边长均为1,点A , B , C都在格点上,以A为圆心,AB为半径画弧,交最上方的网格线于点D , 则CD的长为( )
 A、 B、 C、2.2 D、33. 如图在一个高为米,长为米的楼梯表面铺地毯,则地毯至少需要( )
A、 B、 C、2.2 D、33. 如图在一个高为米,长为米的楼梯表面铺地毯,则地毯至少需要( )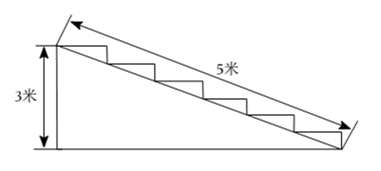 A、米 B、米 C、米 D、米4. 如图,在中, . 按以下步骤作图:①以点为圆心,适当长为半径画弧,分别交 , 于点 , ;②分别以 , 为圆心,大于的长为半径画弧,两弧在内交于点;③作射线 . 若 , 为边的中点,为射线上一动点,则的最小值为( )
A、米 B、米 C、米 D、米4. 如图,在中, . 按以下步骤作图:①以点为圆心,适当长为半径画弧,分别交 , 于点 , ;②分别以 , 为圆心,大于的长为半径画弧,两弧在内交于点;③作射线 . 若 , 为边的中点,为射线上一动点,则的最小值为( ) A、3 B、 C、 D、55. 如图,由六个边长为的小正方形构成一个大长方形,连接小正方形的三个顶点,可得到 , 则中边上的高是( )
A、3 B、 C、 D、55. 如图,由六个边长为的小正方形构成一个大长方形,连接小正方形的三个顶点,可得到 , 则中边上的高是( )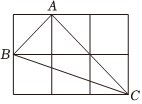 A、 B、 C、 D、6. 如图,长方形中, , , 在数轴上,若以点为圆心,的长为半径作弧交数轴于点 , 则点表示的数为
A、 B、 C、 D、6. 如图,长方形中, , , 在数轴上,若以点为圆心,的长为半径作弧交数轴于点 , 则点表示的数为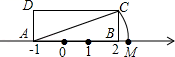 A、 B、 C、2 D、7. 如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=4,BF=2,△ADG的面积为 , 则点F到BC的距离为( )
A、 B、 C、2 D、7. 如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=4,BF=2,△ADG的面积为 , 则点F到BC的距离为( )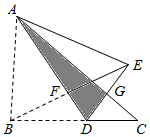 A、 B、 C、 D、8. 如图,在中,平分交于点 , 则点到的距离是( )
A、 B、 C、 D、8. 如图,在中,平分交于点 , 则点到的距离是( )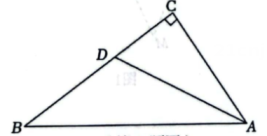 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
9. 2002年在北京石开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.如图,弦图是由四个能够重合的直角三角形与一个小正方形拼成的一个大正方形.若 , , 则小正方形的面积为 .
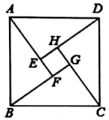 10. 如图:在△ABC中,CE平分∠ACB , CF平分∠ACD , 且EF∥BC交AC于M , 若CM=5,则CE2+CF2= .
10. 如图:在△ABC中,CE平分∠ACB , CF平分∠ACD , 且EF∥BC交AC于M , 若CM=5,则CE2+CF2= .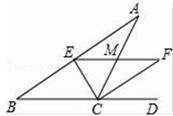 11. 如图,在中, , , . 点D为外一点,满足 , , 则的面积是 .
11. 如图,在中, , , . 点D为外一点,满足 , , 则的面积是 . 12. 如图,在和中, , 点在边的中点上,若 , , 连结 , 则的长为 .
12. 如图,在和中, , 点在边的中点上,若 , , 连结 , 则的长为 .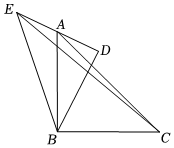 13. 如图,和都是等腰直角三角形, , 点在边上,与交于点 , 若 , 记的面积为 , 的面积为 , 则.
13. 如图,和都是等腰直角三角形, , 点在边上,与交于点 , 若 , 记的面积为 , 的面积为 , 则.
三、解答题
-
14. 数学家波利亚说过:“为了得到一个方程,我们必须把同一个量用两种不同的方法表示出来,即将一个量算两次,从而建立等量关系.”类似的,我们可以用两种不同的方法来表示同一个图形的面积,从而得到一个等式.
 (1)、如图 , 大正方形是由两个小正方形和两个形状大小完全相同的长方形拼成,请用两种不同的方法表示图中大正方形的面积.
(1)、如图 , 大正方形是由两个小正方形和两个形状大小完全相同的长方形拼成,请用两种不同的方法表示图中大正方形的面积.方法:;方法:;根据以上信息,可以得到的等式是;
(2)、如图 , 大正方形是由四个边长分别为的直角三角形(为斜边)和一个小正方形拼成,请用两种不同的方法分别表示小正方形的面积,并推导得到之间的数量关系;(3)、在()的条件下,若 , 求斜边的值.15. 已知, , , 是从点出发的三条线段,且 . (1)、如图①,若点在线段上,连接 , , 试判断的形状,并说明理由.(2)、如图②,连接 , , , 且与相交于点 , 若 , , , 求和的长.
(1)、如图①,若点在线段上,连接 , , 试判断的形状,并说明理由.(2)、如图②,连接 , , , 且与相交于点 , 若 , , , 求和的长.四、综合题