2023-2024学年沪科版初中数学七年级下册 10.4 平移同步分层训练培优题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，将网格中的三条线段沿网格线的方向(水平或竖直)平移后组成一个首尾依次相接的三角形，至少需要移动（）

A、12格 B、11格 C、9 格 D、8格

查看试题解析
2. 观察下面图案在A、B、C、D四幅图案中，能通过原图案平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，将三角形 $A B C$ 沿 $A B$ 方向平移至三角形 $D E F$ ，且 $A B = 4$ ， $D B = 1$ ，则 $C F$ 的长为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 如图，用平移方法说明平行四边形的面积公式 $S = a h$ 时，若 $△ A B E$ 平移到 $△ D C F$ ， $a = 4$ ， $h = 3$ ，则 $△ A B E$ 的平移距离为（）

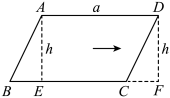A、3 B、4 C、5 D、12

查看试题解析
5. 如图， $△ A B C$ 以每秒3cm的速度沿着射线 $B C$ 向右平移，平移2秒后所得图形是 $△ D E F$ ，如果 $A D = 2 C E$ ，那么 $B C$ 的长是（）

A、9 B、6 C、5 D、3

查看试题解析
6. 如图，在方格纸中，点 $P 、 Q 、 M$ 是正方形网格的格点．若 $M N ∥ P Q$ ，则点 $N$ 可能是（）

A、点 $A$ B、点 $B$ C、点 $C$ D、点 $D$

查看试题解析
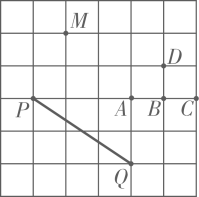7. 如图，点 $A_{1} (1 ， 1)$ ，点 $A_{1} (1 ， 1)$ 向上平移1个单位，再向右平移2个单位．得到 $A_{2}$ ；点 $A_{2}$ 向上平移2个单位，再向右平移4个单位，得到点 $A_{3}$ ；点 $A_{3}$ 向上平移4个单位，再向右平移8个单位，得到点 $A_{4}$ ……按照这个规律得到 $A_{2020}$ ，则点 $A_{2020}$ 的横坐标为（）

A、 $2^{2019}$ B、 $2^{2020} - 1$ C、 $2^{2020}$ D、 $2^{2020} + 1$

查看试题解析
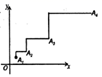8. 如图，长方形ABCD中，AB＝6，第一次平移长方形ABCD沿AB的方向向右平移5个单位长度，得到长方形A₁B₁C₁D₁ ，第2次平移长方形A₁B₁C₁D₁沿A₁B₁的方向向右平移5个单位长度，得到长方形A₂B₂C₂D₂ ， …，第n次平移长方形A_n_－₁B_n_－₁C_n_－₁D_n_－₁沿A_n_－₁B_n_－₁的方向向右平移5个单位长度，得到长方形A_nB_nC_nD_n（n＞2），若AB_n的长度为2 026，则n的值为（）．

A、407 B、406 C、405 D、404

查看试题解析

二、填空题

9. 如图，在长为80米，宽为60米的长方形地块上，有纵横交错的几条小路（图中阴影部分），宽均为4米，其他部分均种植花草，则种植花草的面积是平方米．

查看试题解析
10. 如图：直角△ABC中，AC=3，BC=4，AB=5，则内部五个小直角三角形的周长为．

查看试题解析
11. 如图，某酒店重新装修后，准备在大厅主楼梯上铺设红色地毯，其侧面如图所示，则需地毯米．

查看试题解析
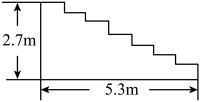12.
如图所示，将△ABC沿直线BC方向平移3个单位得到△DEF，若BC=5，则CF= ．

查看试题解析
13. 如图是一块长方形ABCD的场地，长AB=a米，宽AD=b米，从A、B两处入口的小路宽都为1米，两小路汇合处路宽为2米，其余部分种植草坪，则草坪面积为米² ．

查看试题解析

三、解答题

14.
如图所示是某酒店门前的台阶，现该酒店经理要在台阶上铺上一块红地毯，问这块红地毯至少要多大？

查看试题解析
15.
如图所示，有一条宽相等的小路穿过长方形的草地ABCD ，若AB＝60m，BC＝84m，AE＝100m，若要硬化这条小路，且每平方米造价50元，则需要多少元钱？

查看试题解析

四、综合题

16. 如图，平面直角坐标系中，点A在y轴上，坐标为 $(0 ， 5)$ ，将线段 $O A$ 沿x轴方向平移3个单位得到线段 $C B$ ．点D是线段 $B C$ 上一动点（不与点B，C重合）， $A E$ 平分 $∠ B A D$ ， $O E$ 平分 $∠ C O D$ ， $A E$ 与 $O E$ 交于点E．

(1)、线段 $A B$ 与 $O C$ 有怎样的位置关系和数量关系；
其依据是；
点B的坐标为；

(2)、若 $∠ A D O = 70 °$ ，直接写出 $∠ A E O$ 的度数；

(3)、点D在线段 $B C$ 上运动时（不与点B，C重合），猜想： $∠ A E O$ 与 $∠ A D O$ 有怎样的数量关系，并说明理由．

查看试题解析
17. 在平面直角坐标系xOy中，将点 $M (x ， y)$ 到x轴和y轴的距离的较大值定义为点M的“相对轴距”，记为 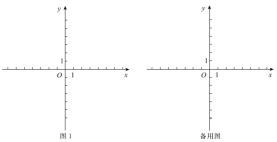$d (M)$ ．即：如果 $| x | \geq | y |$ ，那么 $d (M) = | x |$ ；如果 $| x | < | y |$ ，那么 $d (M) = | y |$ ．例如：点 $M (1 ， 2)$ 的“相对轴距” $d (M) = 2$ ．

(1)、点 $P (- 2 ， 1)$ 的“相对轴距” $d (P) =$ ；

(2)、请在图1中画出“相对轴距”与点 $P (- 2 ， 1)$ 的“相对轴距”相等的点组成的图形；

(3)、已知点 $A (1 ， 1)$ ， $B (2 ， 3)$ ， $C (3 ， 2)$ ，点M，N是 $△ A B C$ 内部（含边界）的任意两点．
①直接写出点M与点N的“相对轴距”之比 $\frac{d (M)}{d (N)}$ 的取值范围；
②将 $△ A B C$ 向左平移 $k (k > 0)$ 个单位得到 $△ A B C$ ，点 $M$ 与点 $N$ 为 $△ A B C$ 内部（含边界）的任意两点，并且点 $M$ 与点 $N$ 的“相对轴距”之比 $\frac{d (M)}{d (N)}$ 的取值范围和点M与点N的“相对轴距”之比 $\frac{d (M)}{d (N)}$ 的取值范围相同，请直接写出k的取值范围．

查看试题解析