2023-2024学年沪科版初中数学七年级下册 10.3 平行线的性质同步分层训练培优题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，把一块含有30°角的三角尺的两个顶点放在直尺的对边上，如果∠1=22°，那么∠2的度数是（）

A、22° B、32° C、38° D、44°

查看试题解析
2. 如图，∠B+∠DCB=180°，AC平分∠DAB，且∠D：∠DAC=5：2，则∠D的度数是（）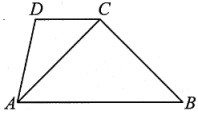

A、100° B、105° C、110° D、120°

查看试题解析
3. 如图，直线 $m ∥ n$ ， ∠1、∠2和∠3的数量关系是（）

A、 $∠ 1 + ∠ 2 + ∠ 3 = 180 °$ B、 $∠ 1 + ∠ 3 - ∠ 2 = 180 °$ C、 $∠ 2 + ∠ 3 - ∠ 1 = 180 °$ D、 $∠ 1 + ∠ 2 = ∠ 3$

查看试题解析
4. 如图，在甲、乙两地之间要修一条笔直的公路，从甲地测得公路的走向是北偏东 $36 °$ ，甲、乙两地同时开工，要使若干天后公路准确接通，乙地所修的公路走向是（）

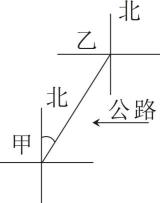A、北偏东 $36 °$ B、南偏西 $36 °$ C、北偏东 $54 °$ D、南偏西 $54 °$

查看试题解析
5. 如图，直线a，b被c，d所截，且a∥b，则下列结论中正确的是（）

A、∠1=∠2 B、∠3=∠4 C、∠2+∠4=180° D、∠1+∠4=180°

查看试题解析
6. 如图，AB∥CD，将一副直角三角尺按如图摆放，∠GEF=60°，∠MNP=45°。有下列结论：①GE∥MP；②∠EFN=150°；③∠BEF=75°；④∠AEG=∠PMN。其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如图1，当光从空气进入水中时，会发生折射，满足入射角∠1 与折射角∠2 的度数比为4：3.如图2，在同一平面上，两条光线同时从空气进入水中，两条入射光线与水面的夹角分别为α，β，水中两条折射光线的夹角为γ，则α，β，γ三者之间的数量关系为（）

A、 $\frac{3}{4} (α + β) = γ$ B、 $\frac{3}{4} (α + β) = 135^{\circ} - γ$ C、α+β=γ D、 $a + β + γ = 180 °$

查看试题解析
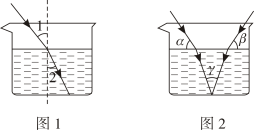8. 下列说法中：①若 $a^{m} = 6$ ， $a^{n} = 3$ ，则 $a^{m - n} = 2$ ；②两条直线被第三条直线所截，一组内错角的角平分线互相平行；③若 $(t - 2)^{2 t} = 1$ ，则 $t = 3$ 或 $t = 0$ ；④已知二元一次方程组 ${\begin{array}{l} x + y = 6 \\ a x + y = 4 \end{array}$ 的解也是二元一次方程 $x - 3 y = - 2$ 的解，则a的值是0.5；其中正确的是（）

A、①② B、②③ C、①④ D、③④

查看试题解析

二、填空题

9. 如图，把块三角板 ABC的直角顶点B放在直线EF 上，∠C=30°，AC∥EF，则∠1 的度数为°.

查看试题解析
10. 如图，一把长方形直尺沿直线断开并错位摆放，点 $E$ 、 $D$ 、 $B$ 、 $F$ 在同一条直线上，若 $∠ A D E = 131 °$ ，则 $∠ D B C$ 的度数为．

查看试题解析
11. 已知，EF∥BC，BE∥CF，现将一副三角尺OAB (∠OAB=45°)和OCD(∠OCD=30°)按如图所示的方式放置，直角顶点O重合，点A，D 在EF 上.若∠1+∠2=70°，∠3 ： ∠4=4 ： 3，则∠DAB的度数为°.

查看试题解析
12. 如图，已知AB∥DE，∠ABC=70°，∠CDE=140°，则∠BCD的度数为.

查看试题解析
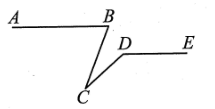13. 已知 $∠ A B C = 60 °$ ， $∠ D E F = 50 °$ ，若 $∠ D E F$ 的一边EF∥BC ，则另一边DE与直线AB相交于点P ，且点E不在直线AB上，则 $∠ A P D$ 的度数为．

查看试题解析

三、解答题

14. 如图，BD是∠ABC的平分线，∠ABE+∠BCF=180°。

(1)、若∠ABC=70°，求∠BCF的值.

(2)、试说明：DE∥CF.

(3)、若CB是∠ACF 的平分线，∠ADB=k∠ABD，求k的值。

查看试题解析
15. 如图，AB∥CD，直线EF与AB，CD分别相交于点G，H，∠EHD=α(0°<α<90°).小安将一个含30°角的直角三角尺PMN按如图1所示的方式放置，使点N，M分别在直线AB，CD上，且在点G，H的右侧，∠P=90°，∠PMN=60°.

(1)、∠PNB+∠PMD∠P(填“>”“<”或“=”).

(2)、如图2，∠MNG的平分线NO交直线CD于点O.
①当NO∥EF∥PM时，求α的度数.
②小安将三角尺PMN保持PM∥EF并向左平移，在平移的过程中求∠MON的度数(用含α的代数式表示).

查看试题解析

四、综合题

16. 已知：点E在线段 $A B ， C D$ 间（如图1）．连接 $B E ， D E$ ． $∠ B E D = ∠ A B E + ∠ C D E$ ．

(1)、求证： $A B ∥ C D$ ．

(2)、如图2，点F在点E右侧．连接 $F B ， F D$ ．求证 $∠ A B F + ∠ B F D + ∠ C D F = 360 °$ ．

(3)、如图3在（2）的条件下，线段 $B E$ ， $F D$ 的延长线交于点H ． $B H$ 交 $C D$ 于点K ．当 $B E$ 平分 $∠ A B F$ ， $D E$ 平分 $∠ C D F$ ， $3 ∠ B F D = 2 ∠ B E D$ ， $∠ B K D + ∠ H D K = 123 °$ 时，求 $∠ B H F$ 的度数．

查看试题解析
17. 如图，直线 $A B ∥ C D$ ，直线 $E F$ 与 $A B$ ， $C D$ 分别交于点 $G ， H$ ， $∠ E H D = α (0 ° < α < 90 °)$ ．小安将直角三角板 $P M N$ （ $∠ P = 90 °$ ， $∠ P M N = 60 °$ ）按如图1放置，使点 $N ， M$ 分别在直线 $A B ， C D$ 上，且 $P M ∥ E F$ ．

(1)、填空： $∠ P N B + ∠ P M D$ $∠ P$ （填“ $>$ ”“ $<$ ”或“=”）．

(2)、如图2， $∠ M N G$ 的平分线 $N O$ 交直线 $C D$ 于点 $O$ ．
①当 $N O ∥ E F$ 时，求 $α$ 的度数；

②小安将三角板 $P M N$ 沿直线 $A B$ 左右移动，保持 $P M ∥ E F$ ，点 $N ， M$ 分别在直线 $A B$ 和直线 $C D$ 上移动，请直接写出 $∠ M O N$ 的度数（用含 $α$ 的式子表示）．

查看试题解析