2023-2024学年沪科版初中数学七年级下册 10.1 相交线同步分层训练培优题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 如图， $A B$ 与 $C D$ 相交于点 $O$ ， $O E ⊥ A B$ ，垂足为 $O$ ，若 $∠ C O E = 44 °$ ，则 $∠ A O D =$ （）

A、44° B、46° C、134° D、136°

查看试题解析
2. 如图，点O在直线AB上，OC⊥AB，OE⊥OF，若∠AOE=45.2°，则∠COF=（）

A、45°12´ B、45°20´ C、44°48´ D、44°80´

查看试题解析
3. 如图，某村庄要在河岸上建一个水泵房引水到C处.他们的做法是：过点C作 $C D ⊥ l$ 于点D ，将水泵房建在了D处，这样做最节省水管长度，其数学原理是（）

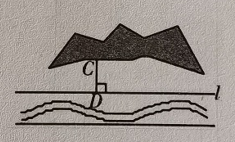A、两点确定一条直线 B、垂线段最短 C、两点之间，线段最短 D、过一点有且仅有一条直线与已知直线垂直

查看试题解析
4. 甲从 $O$ 点出发，沿北偏西 $30 °$ 走了 $50$ 米到达 $A$ 点，乙从 $O$ 点出发，沿南偏东 $35 °$ 方向走了 $80$ 米到达 $B$ 点，则 $∠ A O B$ 为（）

A、 $65 °$ B、 $115 °$ C、 $175 °$ D、 $185 °$

查看试题解析
5. 如图1，汉代初期的《淮南万毕术》是中国古代有关物理、化学的重要文献，书中记载了我国古代学者在科学领域做过的一些探索及成就．其中所记载的“取大镜高悬，置水盆于其下，则见四邻矣”，是古人利用光的反射定律改变光路的方法，即“反射光线与入射光线、法线在同一平面上；反射光线和入射光线位于法线的两侧；反射角等于入射角”．为了探清一口深井的底部情况，运用此原理，如图在井口放置一面平面镜可改变光路，当太阳光线 $A B$ 与地面 $C D$ 所成夹角 $∠ A B C = 50 °$ 时，要使太阳光线经反射后刚好垂直于地面射入深井底部，则需要调整平面镜 $E F$ 与地面的夹角 $∠ E B C =$ （）

A、 $60 °$ B、 $70 °$ C、 $80 °$ D、 $85 °$

查看试题解析
6. 在同一平面内，我们把两条直线相交将平面分得的区域数记为 $a_{1}$ ，三条直线两两相交最多将平面分得的区域数记为 $a_{2}$ ，四条直线两两相交最多将平面分得的区域数记为 $a_{3} ， \cdot \cdot \cdot ， (n + 1)$ 条直线两两相交最多将平面分得的区域数记为 $a_{n}$ ，若 $\frac{1}{a_{1} - 1} + \frac{1}{a_{2} - 1} + \cdot \cdot \cdot + \frac{1}{a_{n} - 1} = \frac{10}{11}$ ，则 $n =$ （）

A、 $10$ B、 $11$ C、 $20$ D、 $21$

查看试题解析
7. 如图，把小河里的水引到田地A处，若使水沟最短，则过点A向河岸l作垂线，垂足为点B，沿AB挖水沟即可，理由是（　　）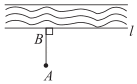

A、两点之间，线段最短 B、垂线段最短 C、两点确定一条直线 D、过一点可以作无数条直线

查看试题解析
8. 如图，直线 $A B ， C D$ 相交于点O， $O A$ 平分 $∠ E O C$ ，若 $∠ E O C = 80 °$ ，则 $∠ B O D$ 的度数为（）

A、 $30 °$ B、 $40 °$ C、 $80 °$ D、 $100 °$

查看试题解析

二、填空题

9. 如图，直线AB，CD交于点O，∠AOC：∠COE=1：2．若∠BOD=28°，则∠COE等于度．

查看试题解析
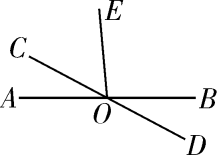10. 如图，直线EF分别交∠AOB的两边于C，D两点，图中有对对顶角，分别是

查看试题解析
11. 如图，直线AB与CD相交于点O，OE⊥CD，OF平分∠AOE，∠COF＝34°，则∠BOD的度数为．

查看试题解析
12. 观察下列各图，寻找对顶角（不含平角）．如图1，图中有2条直线相交，则对顶角有对；如图2，图中有3条直线相交于一点，则对顶角有对；如图3图中有 $n$ 条直线相交于一点，则对顶角有对．

查看试题解析
13. 如图，平面中两条直线 $l_{1}$ 和 $l_{2}$ 相交于点 $O$ ，对于平面上任意一点 $M$ ，若点 $M$ 到直线 $l_{1}$ 、 $l_{2}$ 的距离分别是 $p c m$ 、 $q c m$ ，则称有序实数对 $(p ， q)$ 是点 $M$ 的“距离坐标” $.$ 特别地，当点在直线上时，定义点到直线的距离为 $0 .$ 下列说法：
$①$ “距离坐标”是 $(0 ， 0)$ 的点只有点 $O$ ；
$②$ “距离坐标”是 $(0 ， 1)$ 的点只有 $1$ 个；
$③$ “距离坐标”是 $(2 ， 2)$ 的点共有 $4$ 个；
正确的有 $($ 填序号 $)$ ．

查看试题解析

三、解答题

14. 如图所示，直线a，b，c两两相交，∠1＝2∠3，∠2＝65°，求∠4的度数.

查看试题解析
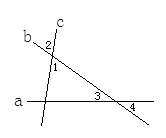15. 如图，O为直线 $A B$ 上一点， $∠ A O C = 50 °$ ， $O D$ 平分 $∠ A O C$ ， $∠ D O E = 90 °$ ．

(1)、请你数一数，图中有多少个小于平角的角；

(2)、求出 $∠ B O D$ 的度数；

(3)、试判断 $O E$ 是否平分 $∠ B O C$ ，并说明理由。

查看试题解析

四、综合题

16. 观察下列各图，寻找对顶角（不含平角）、邻补角．

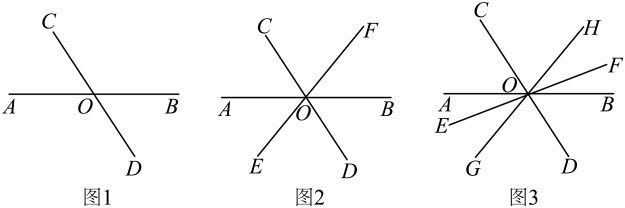(1)、如图1，共有对对顶角，对邻补角；

(2)、如图2，共有对对顶角，对邻补角；

(3)、如图3，共有对对顶角，对邻补角；

(4)、根据（1）-（3）中直线的条数与对顶角、邻补角的对数之间的关系，探究：若有 $n$ 条直线相交于一点，则可形成多少对对顶角？多少对邻补角？

查看试题解析
17. 如图1，大课间的广播操展让我们充分体会到了一种整体的图形之美，洋洋和乐乐想从数学角度分析下如何能让班级同学们的广播操做得更好，他们搜集了标准广播操图片进行讨论，如图2，为了方便研究，定义两手手心位置分别为A ， B两点，两脚脚跟位置分别为C ， D两点，定义A ， B ， C ， D平面内O为定点，将手脚运动看作绕点O进行旋转：

(1)、填空：如图2，A ， O ， B三点共线，且∠AOC＝∠BOC ，则∠AOC＝°；

(2)、第三节腿部运动中，如图3，洋洋发现，虽然A ， O ， B三点共线，却不在水平方向上，且∠AOD：∠BOC＝3：2．他经过计算发现，∠AOC﹣ $\frac{2}{3}$ ∠BOD的值为定值，请判断洋洋的发现是否正确，如果正确请求出这个定值，如果不正确，请说明理由；

(3)、第四节体侧运动中，乐乐发现，两腿左右等距张开且∠COD＝30°，开始运动前A、O、B三点在同一水平线上，OA、OB绕点O顺时针旋转，OA旋转速度为50°/s ， OB旋转速度为25°/s ，当OB旋转到与OD重合时，运动停止，如图4．
①运动停止时，直接写出∠AOD＝　▲　；
②请帮助乐乐求解运动过程中∠AOC与∠BOE的数量关系．

查看试题解析