2023-2024学年沪科版初中数学七年级下册 10.1 相交线同步分层训练基础题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，直线AB，CD相交于点E， $E F ⊥ A B$ 于E，若 $∠ C E F = 65 °$ ，则∠DEB的度数为（）．

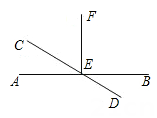A、155° B、135° C、35° D、25°

查看试题解析
2. 如图，直线l表示一段河道，点P表示水池，现要从河l向水池P引水，设计了四条水渠开挖路线PA，PB，PC，PD，其中PB⊥l，要使挖渠的路线最短，可以选择的路线是（　　）

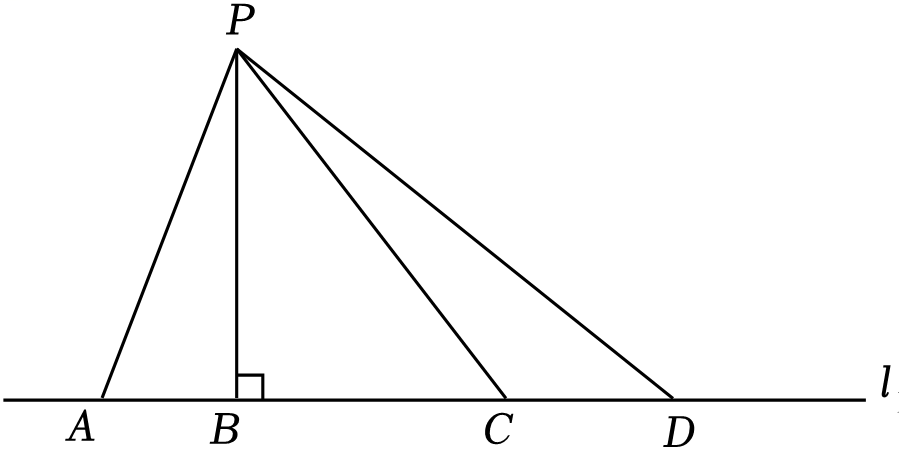A、PA B、PB C、PC D、PD

查看试题解析
3. 如图是小周同学在校运会上投掷实心球的场景，当投掷完毕时，测量员选取AB的长度作为小周的成绩，其依据是（）．

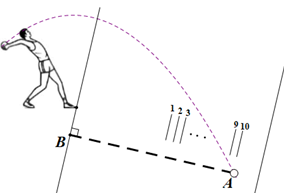A、垂线段最短 B、两点之间线段最短 C、两点确定一条直线 D、过一点有且只有一条直线与已知直线垂直

查看试题解析
4. 下列生活实例中，数学原理解释错误的是（）

A、测量两棵树之间的距离，要拉直皮尺，应用的数学原理是：两点之间，线段最短 B、用两颗钉子就可以把一根木条固定在墙上，应用的数学原理是：两点确定一条直线 C、测量跳远成绩，应用的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短 D、从一条河向一个村庄引一条最短的水渠，应用的数学原理是：在同一平面内，过一点有且只有一条直线与已知直线垂直

查看试题解析
5. 如图，已知O是直线AB上一点，∠1＝40°，OD平分∠BOC ，则∠2＝（　　）

A、70° B、60° C、55° D、45°

查看试题解析
6. 如图，直线DE与BC相交于点O ， $∠ C O E$ 与 $∠ A O E$ 互余， $∠ B O D = 35 °$ ，则 $∠ A O E$ 的度数是（）

A、35° B、45° C、55° D、65°

查看试题解析
7. 如图，某村庄要在河岸 $l$ 上建一个水泵房引水到 $C$ 处．他们的做法是：过点 $C$ 作 $C D ⊥ l$ 于点D，将水泵房建在了D处，这样做最节省水管长度，其数学道理是（）

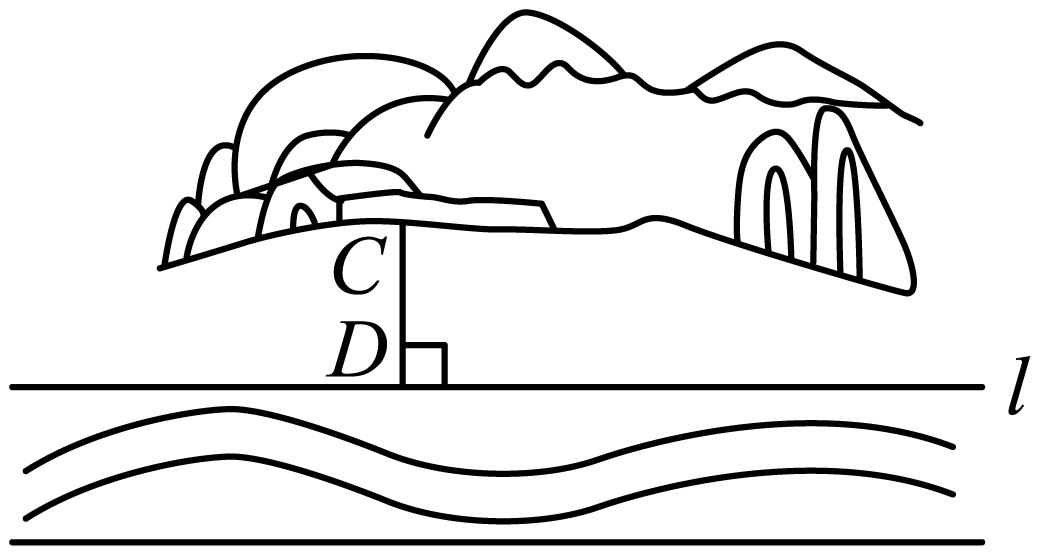A、两点确定一条直线 B、垂线段最短 C、两点之间，线段最短 D、过一点有且仅有一条直线与已知直线垂直

查看试题解析
8. 如图，点 $A$ ， $D$ 在直线 $m$ 上，点 $B$ ， $C$ 在直线 $n$ 上， $A B ⊥ n$ ， $A C ⊥ m$ ， $B D ⊥ m$ ，点 $A$ 到直线 $B D$ 的距离是（）

A、线段 $A D$ 的长度 B、线段 $B C$ 的长度 C、线段 $A B$ 的长度 D、线段 $B D$ 的长度

查看试题解析

二、填空题

9. 如图，点 $O$ 在直线 $A B$ 上， $O C ⊥ O D$ ，若 $∠ C O B = 60 °$ ，则 $∠ A O D$ 的大小为 $° .$

查看试题解析
10. 如图，直线 $l_{1}$ 与 $l_{2}$ 相交于点O， $O M ⊥ l_{1}$ ，若 $∠ α = 44 °$ ，则 $∠ β =$ ；

查看试题解析
11. 如图，运动会上，小明自踏板M处跳到沙坑P处，甲、乙、丙三名同学分别测得PM＝3.25米，PN＝3.15米，PF＝3.21米，则小明的成绩为米．（填具体数值）

查看试题解析
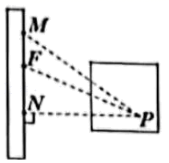12. 两条直线相交，只有1个交点，三条直线相交，最多有3个交点，四条直线相交，最多有6个交点，10条直线相交，最多有个交点.

查看试题解析
13. 下列三个日常现象：
其中，可以用“垂线段最短”来解释的是（填序号）．

查看试题解析

三、解答题

14. 如图，已知直线AB与CD相交于点O，OD平分∠BOE，∠AOE＝126°．

(1)、求∠AOC的度数.

(2)、若直线OF⊥OE，求∠DOF的度数.

查看试题解析
15. 如图，点A ， O ， B在一条直线上， $∠ A O C = 45 °$ ， $∠ A O C = 3 ∠ C O D$ ， $O E$ 平分 $∠ B O D$ ，求 $∠ C O E$ 的度数．
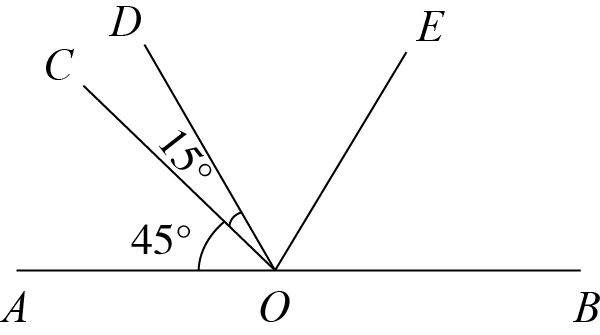
请将以下解答过程补充完整．
解： $∵ ∠ A O C = 45 °$ ， $∠ A O C = 3 ∠ C O D$ ．
$∴ ∠ C O D =$     ▲    °，
$∴ ∠ A O D = ∠$     ▲     $+ ∠$     ▲     $=$     ▲    °．
∵点A ， O ， B在一条直线上，
$∴ ∠ B O D =$     ▲    ° $- ∠ A O D =$     ▲    °．
$∵ O E$ 平分 $∠ B O D$ ，
$∴ ∠$     ▲     $= \frac{1}{2} ∠ B O D =$     ▲    °．
$∴ ∠ C O E = ∠ C O D + ∠$     ▲    =    ▲    °．

查看试题解析

四、综合题

16. 如图，点O是直线AB上一点，射线OC、OD、OE在直线AB的同一侧，且OC平分∠AOE，OD⊥OC．

(1)、如果∠COE=40°，求∠AOD的度数．

(2)、如果∠AOE+30°=∠BOE，求∠BOD的度数．

查看试题解析
17. 如图， $∠ 1 = 36 °$ ， $A B ⊥ C D$ ，垂足为O， $E F$ 经过点O．

(1)、写出 $∠ A O E$ 的邻补角， $∠ C O E$ 的对顶角．

(2)、求 $∠ 2$ 的度数．

查看试题解析