沪科版初中数学七年级下册 8.3 完全平方公式与平方差公式同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 下面计算正确的是( )A、(a+1)2=a2+1 B、(a2)3﹣a8÷a4=a4 C、(m2n)3•m2n=m8n4 D、(12a2b2c﹣4a2b)÷4a2b=3bc2. 计算____.A、 B、 C、 D、3. 若一个正整数能表示为两个连续奇数的平方差,则称这个正整数为“好数”.下列正整数中能称为“好数”的是( )A、205 B、250 C、502 D、5204. 如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
 A、(a﹣b)2=a2﹣2ab+b2 B、(a+b)2=a2+2ab+b2 C、a2﹣b2=(a+b)(a﹣b) D、a2+ab=a(a+b)5. 如图分割的正方形,拼接成长方形的方案中,可以验证( )
A、(a﹣b)2=a2﹣2ab+b2 B、(a+b)2=a2+2ab+b2 C、a2﹣b2=(a+b)(a﹣b) D、a2+ab=a(a+b)5. 如图分割的正方形,拼接成长方形的方案中,可以验证( ) A、 B、 C、 D、6. 在边长为a的正方形中挖去一个边长为b的小正方形( )(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
A、 B、 C、 D、6. 在边长为a的正方形中挖去一个边长为b的小正方形( )(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )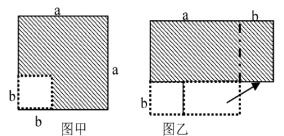 A、 B、 C、 D、7. 如图,在长方形ABCD中,AB=6,BC=10,其内部有边长为a的正方形AEFG与边长为b的正方形HIJK,两个正方形的重合部分也为正方形,且面积为5.若右侧阴影部分的面积S2是左侧阴影部分面积S1的4倍,则正方形AEFG与正方形HIJK的面积之和为( )
A、 B、 C、 D、7. 如图,在长方形ABCD中,AB=6,BC=10,其内部有边长为a的正方形AEFG与边长为b的正方形HIJK,两个正方形的重合部分也为正方形,且面积为5.若右侧阴影部分的面积S2是左侧阴影部分面积S1的4倍,则正方形AEFG与正方形HIJK的面积之和为( )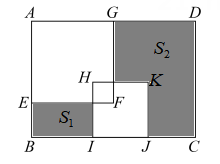 A、20 B、25 C、 D、8. 有个依次排列的整式:第项是 , 用第项乘 , 所得之积记为 , 将第项加上得到第项,再将第项乘得到 , 将第项加上得到第项以此类推,某数学兴趣小组对此展开研究,得到下列个结论:
A、20 B、25 C、 D、8. 有个依次排列的整式:第项是 , 用第项乘 , 所得之积记为 , 将第项加上得到第项,再将第项乘得到 , 将第项加上得到第项以此类推,某数学兴趣小组对此展开研究,得到下列个结论:
第项为;
;
若第项的值为 , 则 .
以上结论正确的个数为( )A、个 B、个 C、个 D、个二、填空题
-
9. 已知:x2﹣y2=2023,且x﹣y=2023,则x+y= .10. 若4x2+kx+25是一个完全平方式,则k的值是 .11. 已知 , 则的值是 .12. 用如图1所示的张长为 , 宽为()的小长方形纸片,按图的方式不重叠地放在矩形内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为 , 当的长度发生变化时,按照同样的放置方式,始终保持不变.则 , 之间满足的关系式为 .
 13. 一个三位数A . 它的各个数位上的数字均不为零,且满足百位上数字与个位上数字的和等于十位上数字的两倍,则称这个三位数为“三好数”,将“三好数”A的百位数字与个位数字交换位置后得到的新数记为 , 另记A和的和为 . 例如:246满足 , 则246是“三好数”,且 , 则134(选填“是”或“不是”)“三好数”;已知“三好数”M的百位数字小于个位数字,且能被8整除,则满足条件的“三好数”M的最大值为 .
13. 一个三位数A . 它的各个数位上的数字均不为零,且满足百位上数字与个位上数字的和等于十位上数字的两倍,则称这个三位数为“三好数”,将“三好数”A的百位数字与个位数字交换位置后得到的新数记为 , 另记A和的和为 . 例如:246满足 , 则246是“三好数”,且 , 则134(选填“是”或“不是”)“三好数”;已知“三好数”M的百位数字小于个位数字,且能被8整除,则满足条件的“三好数”M的最大值为 .三、解答题
-
14. 观察下列等式,回答问题.
;
;
;
;
(1)、试求的值;(2)、判断的值的个位数字是几?15. 如图1,长方形ABCD的边长分别为a,b,请观察图形,解答下列问题: (1)、若用四个完全相同的长方形ABCD拼成如图2所示的正方形,请写出代数式(a+b)2 , (a-b)2 , ab之间的等量关系:(2)、根据(1)中的等量关系解决问题:若x+y=7,xy=6,求x-y的值.(3)、若以长方形ABCD的各边为一边向外作正方形(如图3),且四个正方形的周长之和为32,四个正方形的面积之和为20,求长方形ABCD的面积.
(1)、若用四个完全相同的长方形ABCD拼成如图2所示的正方形,请写出代数式(a+b)2 , (a-b)2 , ab之间的等量关系:(2)、根据(1)中的等量关系解决问题:若x+y=7,xy=6,求x-y的值.(3)、若以长方形ABCD的各边为一边向外作正方形(如图3),且四个正方形的周长之和为32,四个正方形的面积之和为20,求长方形ABCD的面积.四、综合题
-
16. 用几个小的长方形、正方形拼成一个大的正方形,然后利用两种不同的方法计算这个大的正方形的面积,可以得到一个等式例如:计算图的面积,把图看作一个大正方形它的面积是;如果把图看作是由个长方形和个小正方形组成的,它的面积为 , 由此得到 .
 (1)、如图 , 由几个面积不等的小正方形和几个小长方形拼成一个边长为的正方形,从中你能发现什么结论?该结论用等式表示为 .(2)、利用(1)中的结论解决以下问题:
(1)、如图 , 由几个面积不等的小正方形和几个小长方形拼成一个边长为的正方形,从中你能发现什么结论?该结论用等式表示为 .(2)、利用(1)中的结论解决以下问题:已知 , , 求的值;
(3)、如图 , 正方形边长为 , 正方形边长为 , 点 , , 在同一直线上,连接、 , 若 , , 求图中阴影部分的面积.17. 对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式.例如由图1可以得到 , 这样就用图形面积验证了完全平方公式. (1)、类似地,写出图2中所表示的数学等式为;(2)、如图3,用不同的代数式表示大正方形的面积,由此得到的数学等式为;(3)、利用上面(2)的结论解决问题:若 , 求的值;(4)、利用此方法也可以求出一些不规则图形的面积.如图4,将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接和 , 若这两个正方形的边长满足 , , 请求出阴影部分的面积.
(1)、类似地,写出图2中所表示的数学等式为;(2)、如图3,用不同的代数式表示大正方形的面积,由此得到的数学等式为;(3)、利用上面(2)的结论解决问题:若 , 求的值;(4)、利用此方法也可以求出一些不规则图形的面积.如图4,将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接和 , 若这两个正方形的边长满足 , , 请求出阴影部分的面积.