2023-2024学年沪科版初中数学七年级下册 8.3 完全平方公式与平方差公式同步分层训练基础题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 下列运算结果正确的是（）

A、2a+3a＝5a² B、（﹣ab²）³＝﹣a³b⁶ C、a³•a³＝a⁹ D、（a+2b）²＝a²+4b²

查看试题解析
2. 下列多项式的乘法中可用平方差公式计算的是（）

A、(1+x)(x+1) B、(-a+b)(a-b) C、(x²-y)(y²+x) D、 $(\frac{1}{2} a + b) (b - \frac{1}{2} a)$

查看试题解析
3. 如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的长方形.根据图形的变化过程写出的一个正确的等式为（）

A、 $a^{2} - 2 a b + b^{2} = (a - b)^{2}$ B、 $a^{2} - a b = a (a - b)$ C、 $a^{2} - b^{2} = (a - b)^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
4. 从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后，将其截成四个相同的等腰梯形（如图甲），然后拼成一个平行四边形（如图乙），那么通过计算两个图形阴影部分的面积，可以验证成立的式子为（）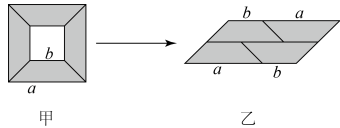

A、(a+b)²=a²+2ab+b² B、(a- b)²= a²-2ab+b² C、a²- b²=(a+b) (a- b) D、(a+2b) (a+b)= a²+3ab+2b²

查看试题解析
5. 如图，用不同的代数式表示图中阴影部分的面积，可得等式（）

A、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ B、 ${(a - b)}^{2} = a^{2} + 2 a b - b^{2}$ C、 $(a + b) (a - b) = a^{2} - b^{2}$ D、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

查看试题解析
6. 如图为2024年某月日历，现用一个正方形方框框住部分（阴影部分）9个位置上的数，若最小的数与最大的数的积记为n，中间位置上的数记为m．下列所给的数据中，n不可能是（）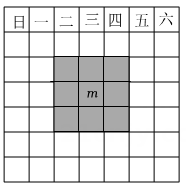

A、377 B、420 C、465 D、512

查看试题解析
7. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式．例如，利用图1可以得到 $a (a + b) = a^{2} + a b$ ，那么利用图2所得到的数学等式为（）

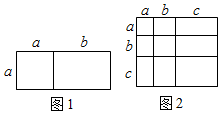A、 ${(a + b + c)}^{2} = a^{2} + b^{2} + c^{2}$ B、 ${(a + b + c)}^{2} = 2 a^{2} + 2 b^{2} + 2 c^{2}$ C、 ${(a + b + c)}^{2} = a^{2} + b^{2} + c^{2} + a b + b c + c a$ D、 ${(a + b + c)}^{2} = a^{2} + b^{2} + c^{2} + 2 a b + 2 b c + 2 c a$

查看试题解析
8. 我国宋代数学家杨辉发现了 ${(a + b)}^{n}$ （ $n = 0$ ， 1，2，3，…）展开式系数的规律：
以上系数三角表称为“杨辉三角”，根据上述规律， ${(a + b)}^{8}$ 展开式的系数和是（）

A、64 B、128 C、256 D、612

查看试题解析

二、填空题

9. 若x²﹣kx+4是一个完全平方式，则k的值是．

查看试题解析
10. 计算：

(1)、(3a²)²a⁵=.

(2)、(y³)²÷y⁸=.

(3)、-(-2a²)⁴= ．

查看试题解析
11. 某农户租两块土地种植沃柑，第一块是边长为 $a m$ 的正方形，第二块是长为 $(a + 10) m$ ，宽为 $(a + 5) m$ 的长方形，则第二块比第一块的面积多了 $m^{2}$ ．

查看试题解析
12. 已知 $2 x^{2} - 3 x - 2 = 0$ ．则 $x^{2} + \frac{1}{x^{2}} =$ ．

查看试题解析
13. 若 $a - b = 1 ， a^{2} + b^{2} = 25 ，则 a b =$

查看试题解析

三、解答题

14. 图1是一个长为 $2 x$ 、宽为 $2 y$ 的长方形，沿图中虚线用剪刀剪成四个完全相同的小长方形，然后按图2所示拼成一个正方形．

(1)、对于图2整体大正方形的面积，可以用两种方法表示：
方法一：按照正方形面积公式表示为；
方法二：按照四个小长方形面积+阴影正方形面积表示为，则根据面积相等，可得等式；

(2)、若 $x + y = 4$ ， $x y = 3$ ，求 ${(x - y)}^{2}$ ．

查看试题解析
15. 现有长为a ，宽为b的长方形卡片（如图①）若干张，某同学用4张卡片拼出了一个大正方形（不重叠、无缝隙，如图②）．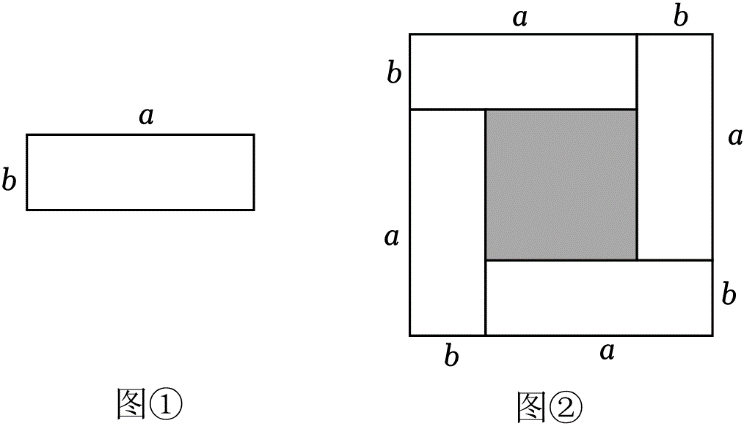

(1)、图②中，大正方形的边长是，阴影部分正方形的边长是．（用含a ， b的式子表示）

(2)、用两种方法表示图②中阴影部分正方形的面积（不化简），并用一个等式表示（a+b）² ，（a﹣b）² ， ab三者之间的数量关系．

(3)、已知a+b＝8，ab＝7，求图②中阴影部分正方形的边长．

查看试题解析

四、综合题

16. 如图，从一个长方形铁皮中剪去一个小正方形．

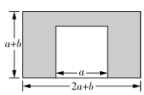(1)、请你用含有a，b的式子表示阴影部分的面积．

(2)、当a=7米，b=2米时，求阴影部分的面积．

查看试题解析
17. 数学课上，老师用图1中的一张边长为a的正方形纸片A，1张边长为b的正方形纸片B和2张宽与长分别为a与b的长方形纸片C，拼成了如图2所示的大正方形，观察图形并解答下列问题：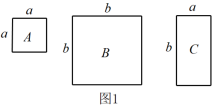

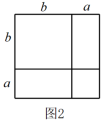
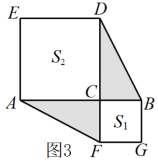(1)、由图1和图2可以得到的等式为（用含a，b的等式表示）；

(2)、莉莉想用这三种纸片拼出一个面积为 $(2 a + b) (a + 2 b)$ 的大长方形，求需A，B，C三种纸片各多少张；

(3)、如图3，S₁ ， S₂分别表示边长为p，q的正方形的面积，且A，B，C三点在一条直线上， $S_{1} + S_{2} = 20$ ， $p + q = 6$ ．求图中阴影部分的面积．

查看试题解析