2023-2024学年沪科版初中数学七年级下册 8.2 整式乘法同步分层训练培优题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 下列运算正确的是（）

A、 $x^{2} + x^{2} = x^{4}$ B、 $3 a^{3} \cdot 2 a^{2} = 6 a^{6}$ C、 $2 x^{4} \cdot (- 3 x^{4}) = 6 x^{8}$ D、 ${(- a^{2})}^{3} = - a^{6}$

查看试题解析
2. 若 $(x - 1) (x + m) = x^{2} + 2 x - 3 ，$ 则常数m 的值为（）

A、3 B、2 C、-3 D、-2

查看试题解析
3. 通过计算和比较图1，2 中阴影部分的面积，可以验证的等式为（）

A、a(b-x)=ab-ax B、b(a-x)=ab-bx C、(a-x)(b-x)=ab-ax-bx D、(a-x)(b-x)=ab-ax-bx+x²

查看试题解析
4. 若关于x的多项式 $(x^{2} + a x + 2) (2 x - 4)$ 展开、合并后不含x²项，则a的值是（）

A、0 B、 $\frac{1}{2}$ C、2 D、-2

查看试题解析
5. 已知多项式ax+b与 $2 x^{2} - x + 2$ 的乘积展开式中不含 x的一次项，且常数项为4，则 $a^{b}$ 的值为（）

A、2 B、-2 C、1 D、-1

查看试题解析
6. 如图，现有正方形卡片 A类，B类和长方形卡片C 类若干张，如果要拼一个长为（a+3b）、宽为（a+2b）的大长方形，那么需要C类卡片（）

A、3张 B、4张 C、5张 D、6张

查看试题解析
7. 若把多项式x²+ax+b分解因式，得(x+1）·(x-3)，则a，b的值分别为（）

A、2，3 B、-2，-3 C、-2，3 D、2，-3

查看试题解析
8. 已知a，b，c为非零的实数，则 $\frac{a}{| a |} + \frac{a b}{| a b |} + \frac{a c}{| a c |} + \frac{b c}{| b c |}$ 的可能值的个数为（）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

9. 计算： ${(a^{2} b)}^{2} \div a b =$ ．

查看试题解析
10. 若 $x^{2} + a x + b = (x + 2) (x + 3)$ ，则 $a + b =$ ．

查看试题解析
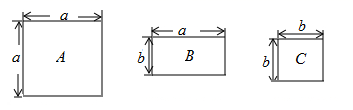
11. 已知一个长方形的面积为4x²+2x，宽为2x，则它的长为.

查看试题解析
12. 现有A、B、C三种型号的地板砖，其规格如图所示，若用这三种地板砖铺设一个长为 $3 a + 2 b$ ，宽为 $a + b$ 的长方形地面，则需要B种地砖块．

查看试题解析
13. 观察、归纳：
（x﹣1）（x+1）＝x²﹣1；

（x﹣1）（x²+x+1）＝x³﹣1；

（x﹣1）（x³+x²+x+1）＝x⁴﹣1；

…

请你根据以上等式的规律，完成下列问题：

⑴（x﹣1）（xⁿ+…+x²+x+1）＝﹣1；

⑵计算：1+2+2²+…+2²⁰¹⁹＝．

查看试题解析

三、解答题

14. 小马和小虎两人共同计算一道整式乘法题： $(3 x + a) (2 x + b)$ ，由于小马抄错了 $b$ 的符号，得到的结果为 $6 x^{2} - 17 x + 12$ ；由于小虎漏抄了第一个多项式中 $x$ 的系数，得到的结果为 $2 x^{2} - 5 x - 12$ ．

(1)、求出 $a$ ， $b$ 的值；

(2)、请你计算出这道整式乘法题的正确结果．

查看试题解析
15. 如图1，长方形的两边长分别为m＋3，m＋13；如图2的长方形的两边长分别为m＋5，m＋7．（其中m为正整数）

(1)、写出并计算两个长方形的面积 $S_{1}$ ， $S_{2}$ ，并比较 $S_{1}$ ， $S_{2}$ 的大小；

(2)、现有一个正方形的周长与图1中的长方形的周长相等．试探究该正方形的面积与长方形的面积的差是否是一个常数，如果是，求出这个常数；如果不是，说明理由；

(3)、在（1）的条件下，若某个图形的面积介于 $S_{1}$ 、 $S_{2}$ 之间（不包括 $S_{1}$ 、 $S_{2}$ ）且面积为整数，这样的整数有且只有19个，求m的值

查看试题解析

四、综合题

16. 对于一些较为复杂的问题，可以先从简单的情形入手，然后归纳出一些方法，再解决复杂问题．

(1)、【简单问题】化简
$(x - 1) (x + 1) =$ ；

(2)、 $(x - 1) (x^{2} + x + 1) =$ ；

(3)、 $(x - 1) (x^{3} + x^{2} + x + 1) =$ ；

(4)、【复杂问题】化简
$(x - 1) (x^{2023} + x^{2022} + x^{2021} + ⋯ + x + 1) =$ ；

(5)、【方法应用】计算
$2^{2023} + 2^{2022} + 2^{2021} + ⋯ + 2 + 1$ ．

查看试题解析
17. 通过一次数学活动我们发现，如果两个两位数的十位数字相同，个位数字的和为10，那么这样的两位数相乘会有如下规律：
      $24 \times 26 = (2 \times 3) \times 100 + 4 \times 6 = 624$

      $52 \times 58 = (5 \times 6) \times 100 + 2 \times 8 = 3016$

      $84 \times 86 = (8 \times 9) \times 100 + 4 \times 6 = 7224$

这组计算蕴含着简算规律：十位数字相同，个位数字和为10的两个两位数相乘，积的末两位数是个位数字的乘积，前几位是十位数字与十位数字加一的乘积．

(1)、若有两个两位数的十位数字相同，个位数字的和为10的两个数的乘积为4221，请你利用小组发现的规律写出这两个数×；

(2)、若设这两个两位数相同的十位数字为a，个位数字分别设为b、d，请你用学过的知识证明十位数字相同，个位数字的和为10的这样的两位数的乘积的一般规律．
证明： $\bar{a b} \cdot \bar{a d} = (10 a + b) (10 a + d)$

      $= 100 a^{2} + 10 a b + 10 a d + b d$

      $= 100 a^{2} +_____+ b d$

      $∵ b + d =$ ，

      $∴ \bar{a b} \cdot \bar{a d} =$

查看试题解析