2024年中考数学真题改编贵州模拟试卷(二)
试卷更新日期:2024-04-02 类型:中考模拟
一、选择题
-
1. 下列各数中是负数的是( )A、﹣2 B、0 C、 D、0.32. 如图,用一个平面去截一个圆锥,截面的形状是( )
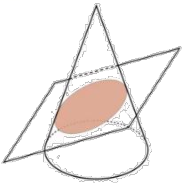 A、
A、 B、
B、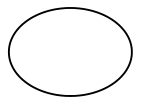 C、
C、 D、
D、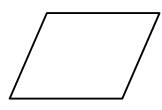 3. 马拉松是国际上非常普及的长跑比赛项目,全程距离26英里385码,折合约为42000米,用科学记数法表示42000为A、 B、 C、 D、4. 如图,菱形ABCD的对角线AC、BD相交于点O , E、F分别是AB、BC边上的中点,连接EF , 着EF= , BD=4,则菱形ABCD的周长为( )
3. 马拉松是国际上非常普及的长跑比赛项目,全程距离26英里385码,折合约为42000米,用科学记数法表示42000为A、 B、 C、 D、4. 如图,菱形ABCD的对角线AC、BD相交于点O , E、F分别是AB、BC边上的中点,连接EF , 着EF= , BD=4,则菱形ABCD的周长为( )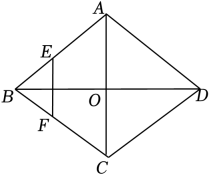 A、4 B、4 C、4 D、285. 要使二次根式有意义,则的值可以为( )A、 B、 C、 D、6. 如果两个相似三角形对应周长之比是2∶3,那么它们的对应边之比是( )A、2∶3 B、4∶9 C、3∶2 D、9∶47. 从数学的观点看,对以下成语及诗句中的事件判断正确的是( )A、成语“守株待兔”是随机事件 B、成语“水中捞月”是随机事件 C、诗句“清明时节雨纷纷”是必然事件 D、诗句“离离原上草,一岁一枯荣”是不可能事件8. 如图,已知AC⊥BC于点C,CD⊥AB于点D,∠A=56°,则∠DCB的度数是( )
A、4 B、4 C、4 D、285. 要使二次根式有意义,则的值可以为( )A、 B、 C、 D、6. 如果两个相似三角形对应周长之比是2∶3,那么它们的对应边之比是( )A、2∶3 B、4∶9 C、3∶2 D、9∶47. 从数学的观点看,对以下成语及诗句中的事件判断正确的是( )A、成语“守株待兔”是随机事件 B、成语“水中捞月”是随机事件 C、诗句“清明时节雨纷纷”是必然事件 D、诗句“离离原上草,一岁一枯荣”是不可能事件8. 如图,已知AC⊥BC于点C,CD⊥AB于点D,∠A=56°,则∠DCB的度数是( )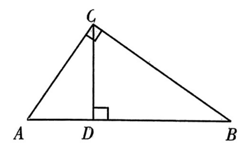 A、30° B、45° C、56° D、60°9. 如图,在中,结合尺规作图的痕迹,已知 , 的周长为14cm,则的周长是( )
A、30° B、45° C、56° D、60°9. 如图,在中,结合尺规作图的痕迹,已知 , 的周长为14cm,则的周长是( ) A、17cm B、18cm C、19cm D、20cm10. 已知点A(-2,y1),B(-1,y2),C(1,y3)均在反比例函数y=的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2≤y3 B、y2<y1<y3 C、y3<y1<y2 D、y3<y2<y111. 小明得到数学课外兴趣小组成员的年龄情况统计如下表,那么对于不同的值,则下列关于年龄的统计量不会发生变化的是( )
A、17cm B、18cm C、19cm D、20cm10. 已知点A(-2,y1),B(-1,y2),C(1,y3)均在反比例函数y=的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2≤y3 B、y2<y1<y3 C、y3<y1<y2 D、y3<y2<y111. 小明得到数学课外兴趣小组成员的年龄情况统计如下表,那么对于不同的值,则下列关于年龄的统计量不会发生变化的是( )年龄(岁)
13
14
15
16
人数(人)
2
15
A、平均数、方差 B、中位数、方差 C、平均数、中位数 D、众数、中位数12. 如图,一次函数与的图像交于点 , 下列结论:①;②;③当时,;④;⑤.所有正确结论的序号为( ) A、①②③ B、①②④ C、②③⑤ D、②④⑤
A、①②③ B、①②④ C、②③⑤ D、②④⑤二、填空题
-
13. 分解因式: .14. 从-2, , , -1,0,2,π这七个数中随机抽取一个数,恰好为负整数的概率为15. 我国古代数学名著《九章算术》中,记载了利用算筹表示方程组的方法,算筹图
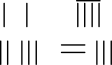 表示的方程组是 . 那么,算筹图
表示的方程组是 . 那么,算筹图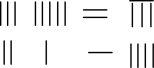 表示的方程组是 . 16. 如图,在矩形中,将绕点逆时针旋转得到 , 使得、、三点恰好在同一直线上,与相交于点 , 连接 , 以下结论正确的是: .
表示的方程组是 . 16. 如图,在矩形中,将绕点逆时针旋转得到 , 使得、、三点恰好在同一直线上,与相交于点 , 连接 , 以下结论正确的是: .;∽;点是线段的黄金分割点; .

三、解答题
-
17. 已知有理数a , b , c在数轴上对应点的位置如图所示:
 (1)、1,b2,2;(填“>”或“<”)(2)、化简: .18. 用两种不同方法解方程:x2-3-2x=019. 为了让初中生更加直观的体验非遗手工技艺,感受非遗文化的独特魅力,培养他们对优秀传统文化的兴趣,积极参与到非物质文化遗产的保护和传承中来,某校举办了非遗知识进课堂活动,选定木偶戏、四面花鼓、说春、船工号子四类非遗项目,随机抽查了部分学生,要求每名学生从中选择自己最喜欢的非遗项目,将抽查结果绘制成如下统计图(不完整).
(1)、1,b2,2;(填“>”或“<”)(2)、化简: .18. 用两种不同方法解方程:x2-3-2x=019. 为了让初中生更加直观的体验非遗手工技艺,感受非遗文化的独特魅力,培养他们对优秀传统文化的兴趣,积极参与到非物质文化遗产的保护和传承中来,某校举办了非遗知识进课堂活动,选定木偶戏、四面花鼓、说春、船工号子四类非遗项目,随机抽查了部分学生,要求每名学生从中选择自己最喜欢的非遗项目,将抽查结果绘制成如下统计图(不完整).
请根据图中信息解答下列问题:
(1)、被抽查的学生人数为 , 并将条形统计图补充完整 . (温馨提醒:请画在答题卡相对应的图上);(2)、若该校共有1200名学生,根据抽查结果,试估计全校最喜欢“木偶戏”的学生人数;(3)、该学校计划选定其中一个非遗项目创建特色课堂,你对具体选择什么项目有没有建议,请写出1条合理性的建议.20. 如图,一次函数的图象与反比例函数的图象交于点 , . (1)、求一次函数的表达式;(2)、已知点 , 试求与的数量关系.21. 我区启动“绿色公园”建设,计划对面积为的区域进行绿化,经投标由甲、乙两个工程队来完成,已知甲工程队完成绿化的面积与乙工程队完成绿化的面积所用的时间相同,若甲工程队每天比乙工程队多绿化 .(1)、求甲、乙两工程队每天各能完成多少面积的绿化;(2)、若甲工程队每天的绿化费用是万元,乙工程队每天的绿化费用是万元,要使这次绿化的总费用不超过30万元,则至少应安排乙工程队绿化多少天?22. 如图所示,在正方形ABCD中,点E在边BC上(点E不与点B重合),连接AE,过点B作BF⊥AE于点F,交CD于点G.
(1)、求一次函数的表达式;(2)、已知点 , 试求与的数量关系.21. 我区启动“绿色公园”建设,计划对面积为的区域进行绿化,经投标由甲、乙两个工程队来完成,已知甲工程队完成绿化的面积与乙工程队完成绿化的面积所用的时间相同,若甲工程队每天比乙工程队多绿化 .(1)、求甲、乙两工程队每天各能完成多少面积的绿化;(2)、若甲工程队每天的绿化费用是万元,乙工程队每天的绿化费用是万元,要使这次绿化的总费用不超过30万元,则至少应安排乙工程队绿化多少天?22. 如图所示,在正方形ABCD中,点E在边BC上(点E不与点B重合),连接AE,过点B作BF⊥AE于点F,交CD于点G. (1)、求证:△ABF∽△BGC;(2)、若AB=2,G是CD的中点,求AF的长.23. 人工海产养殖合作社安排甲、乙两组人员分别前往海面A,B养殖场捕捞海产品.经测量,A在灯塔C的南偏西60°方向,B在灯塔C的南偏东45°方向,且在A的正东方向,AC=3600米.
(1)、求证:△ABF∽△BGC;(2)、若AB=2,G是CD的中点,求AF的长.23. 人工海产养殖合作社安排甲、乙两组人员分别前往海面A,B养殖场捕捞海产品.经测量,A在灯塔C的南偏西60°方向,B在灯塔C的南偏东45°方向,且在A的正东方向,AC=3600米. (1)、求B养殖场与灯塔C的距离.(2)、甲组完成捕捞后,乙组还未完成捕捞,甲组决定前往B处协助捕捞,若甲组航行的平均速度为600米/分钟,请计算说明甲组能否在9分钟内到达B处?(结果精确到1米,参考数据:1.732)24. 如图,在平面直角坐标系中,经过原点 , 点与点 , 点在轴负半轴上,连接 , 且.
(1)、求B养殖场与灯塔C的距离.(2)、甲组完成捕捞后,乙组还未完成捕捞,甲组决定前往B处协助捕捞,若甲组航行的平均速度为600米/分钟,请计算说明甲组能否在9分钟内到达B处?(结果精确到1米,参考数据:1.732)24. 如图,在平面直角坐标系中,经过原点 , 点与点 , 点在轴负半轴上,连接 , 且.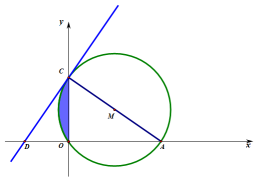 (1)、求的半径;(2)、求证:直线为的切线;(3)、求图中阴影部分的面积.(结果保留和根号).25. 如图所示,已知抛物线经过两点.
(1)、求的半径;(2)、求证:直线为的切线;(3)、求图中阴影部分的面积.(结果保留和根号).25. 如图所示,已知抛物线经过两点. (1)、求拋物线的函数表达式和顶点坐标.(2)、当时,求的取值范围.(3)、若为抛物线上一点.且 , 求出此时点的坐标.26. 综合与实践
(1)、求拋物线的函数表达式和顶点坐标.(2)、当时,求的取值范围.(3)、若为抛物线上一点.且 , 求出此时点的坐标.26. 综合与实践 (1)、【经典再现】人教版八年级数学下册教科书69页14题:如图1,四边形ABCD是正方形,点E是边BC的中点,且EF交正方形外角的平分线CF于点F . 求证AE=EF . (提示:取AB的中点H , 连接HE . )
(1)、【经典再现】人教版八年级数学下册教科书69页14题:如图1,四边形ABCD是正方形,点E是边BC的中点,且EF交正方形外角的平分线CF于点F . 求证AE=EF . (提示:取AB的中点H , 连接HE . )请你思考题中的“提示”,这样添加辅助线的目的是为了构造出≌ , 进而得到AE=EF .
(2)、【类比探究】如图2,四边形ABCD是矩形,且 , 点E是边BC的中点,∠AEF=90°,且EF交矩形外角的平分线CF于点F , 求的值(用含n的式子表示);
(3)、【综合应用】如图3,P为边CD上一点,连接AP , PF , 在(2)的基础上,当 , ∠PAE=45°,PF=时,请直接写出BC的长.