河北省衡水市景县2023-2024学年八年级上学期期末数学试卷
试卷更新日期:2024-04-01 类型:期末考试
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 以下是清华大学、北京大学、上海交通大学、浙江大学的校徽,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算中,正确的是( )A、3x2+2x3=5x5 B、a•a2=a3 C、3a6÷a3=3a2 D、(ab)3=a3b3. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了0.000000023米.用科学记数法表示0.000000023为( )A、23×10﹣10 B、2.3×10﹣10 C、2.3×10﹣9 D、2.3×10﹣84. 现有2cm,3cm,5cm,6cm长的四根木棒,任选其中的三根组成三角形,那么可以组成三角形的个数有( )A、1个 B、2个 C、3个 D、4个5. 下列各式从左到右的变形,是因式分解的是( )A、x2﹣9+6x=(x+3)(x﹣3)+6x B、(x+5)(x﹣2)=x2+3x﹣10 C、x2﹣8x+16=(x﹣4)2 D、6. 如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
2. 下列运算中,正确的是( )A、3x2+2x3=5x5 B、a•a2=a3 C、3a6÷a3=3a2 D、(ab)3=a3b3. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了0.000000023米.用科学记数法表示0.000000023为( )A、23×10﹣10 B、2.3×10﹣10 C、2.3×10﹣9 D、2.3×10﹣84. 现有2cm,3cm,5cm,6cm长的四根木棒,任选其中的三根组成三角形,那么可以组成三角形的个数有( )A、1个 B、2个 C、3个 D、4个5. 下列各式从左到右的变形,是因式分解的是( )A、x2﹣9+6x=(x+3)(x﹣3)+6x B、(x+5)(x﹣2)=x2+3x﹣10 C、x2﹣8x+16=(x﹣4)2 D、6. 如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )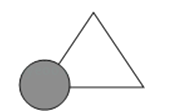 A、SSS B、SAS C、AAS D、ASA7. 等腰三角形的一个角为50°,则这个等腰三角形的底角为( )A、65° B、65°或80° C、50°或65° D、40°8. 下列各式中添括号正确的是( )A、﹣x﹣3y=﹣(x﹣3y) B、2x﹣y=﹣(2x+y) C、8m﹣m2=8m(1﹣m) D、3﹣4x=﹣(4x﹣3)9. 若一个凸多边形的每一个外角都等于36°,则这个多边形的内角和是( )A、1080° B、1260° C、1440° D、1620°10. 如图,直线m是△ABC中BC边的垂直平分线,点P是直线m上一动点,若AB=8,AC=7,BC=9,则△APC周长的最小值是( )
A、SSS B、SAS C、AAS D、ASA7. 等腰三角形的一个角为50°,则这个等腰三角形的底角为( )A、65° B、65°或80° C、50°或65° D、40°8. 下列各式中添括号正确的是( )A、﹣x﹣3y=﹣(x﹣3y) B、2x﹣y=﹣(2x+y) C、8m﹣m2=8m(1﹣m) D、3﹣4x=﹣(4x﹣3)9. 若一个凸多边形的每一个外角都等于36°,则这个多边形的内角和是( )A、1080° B、1260° C、1440° D、1620°10. 如图,直线m是△ABC中BC边的垂直平分线,点P是直线m上一动点,若AB=8,AC=7,BC=9,则△APC周长的最小值是( ) A、15 B、16 C、17 D、15.511. 已知关于x的分式方程的解是正数,则m的取值范围是( )A、m<4且m≠3 B、m<4 C、m≤4且m≠3 D、m>5且m≠612. 如图,两个正方形的边长分别为a和b,如果a﹣b=2,ab=26,那么阴影部分的面积是( )
A、15 B、16 C、17 D、15.511. 已知关于x的分式方程的解是正数,则m的取值范围是( )A、m<4且m≠3 B、m<4 C、m≤4且m≠3 D、m>5且m≠612. 如图,两个正方形的边长分别为a和b,如果a﹣b=2,ab=26,那么阴影部分的面积是( ) A、30 B、34 C、40 D、4413. 如图,若x为正整数,则表示分式的值落在( )
A、30 B、34 C、40 D、4413. 如图,若x为正整数,则表示分式的值落在( ) A、线①处 B、线②处 C、线③处 D、线④处14. 近年来特色农业在我市蓬勃发展,可以向外地运送很多蔬菜,一运送蔬菜车开往距离出发地600千米的目的地,出发第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.2倍匀速行驶,并比原计划提前40分钟到达目的地.设原计划速度为x千米/小时,则方程可列为( )A、 B、 C、 D、15. 在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,连接AD,过点C作CE⊥AD于点E,交AB于点M.过点B作BF⊥BC交CE的延长线于点F,则下列结论正确的有( )(请填序号)
A、线①处 B、线②处 C、线③处 D、线④处14. 近年来特色农业在我市蓬勃发展,可以向外地运送很多蔬菜,一运送蔬菜车开往距离出发地600千米的目的地,出发第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.2倍匀速行驶,并比原计划提前40分钟到达目的地.设原计划速度为x千米/小时,则方程可列为( )A、 B、 C、 D、15. 在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,连接AD,过点C作CE⊥AD于点E,交AB于点M.过点B作BF⊥BC交CE的延长线于点F,则下列结论正确的有( )(请填序号)①△ACD≌△CBF;②∠BDM=∠ADC;③连接AF,则有△ACF是等边三角形;④连接DF,则有AB垂直平分DF.
 A、①②③ B、①②④ C、①③④ D、①④16. 有n个依次排列的整式:第1个整式是x2 , 第2个整式是x2﹣2x+1,用第2个整式减去第1个整式,所得之差记为m1 , 记m2=m1+2;将第2个整式与m2相加作为第3个整式,记m3=m2+2,将第3个整式与m3相加记为第4个整式,以此类推,某数学兴趣小组对此展开研究,将得到四个结论:①m5=﹣2x+9;②当x=3时,第3个整式的值为25;③若第5个整式与第4个整式之差为15,则x=﹣4;④第2024个整式为(x﹣2023)2;⑤当n=100时,;以上正确的结论有( )个.A、1 B、2 C、3 D、4
A、①②③ B、①②④ C、①③④ D、①④16. 有n个依次排列的整式:第1个整式是x2 , 第2个整式是x2﹣2x+1,用第2个整式减去第1个整式,所得之差记为m1 , 记m2=m1+2;将第2个整式与m2相加作为第3个整式,记m3=m2+2,将第3个整式与m3相加记为第4个整式,以此类推,某数学兴趣小组对此展开研究,将得到四个结论:①m5=﹣2x+9;②当x=3时,第3个整式的值为25;③若第5个整式与第4个整式之差为15,则x=﹣4;④第2024个整式为(x﹣2023)2;⑤当n=100时,;以上正确的结论有( )个.A、1 B、2 C、3 D、4二、填空题(本大题共4个小题,共15分.其中17、18、19小题每小题3分,20小题每空2分)
-
17. 若(x﹣2)0=1成立,则x的取值范围是 .18. 计算:1232﹣122×124= .19. 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB为 .
 20. 如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm,如果点P在线段BC上以4cm/秒的速度由B点向C点运动,同时,点Q在线段CD上以a厘米/秒的速度由C点向D点运动,设运动的时间为t秒,
20. 如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm,如果点P在线段BC上以4cm/秒的速度由B点向C点运动,同时,点Q在线段CD上以a厘米/秒的速度由C点向D点运动,设运动的时间为t秒, (1)、BP=厘米,CP=厘米.(用含t的代数式表示)(2)、若以E、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等,则a的值为 .
(1)、BP=厘米,CP=厘米.(用含t的代数式表示)(2)、若以E、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等,则a的值为 .三、解答题(本大题6个小题,共63分.解答应写出文字说明、证明过程或演算步骤)
-
21. 按要求解答下列各题.(1)、分解因式:x3﹣4x2y+4xy2 .(2)、计算:(2y﹣x)(x﹣y)+(2x3y+4xy3)÷2xy.(3)、解分式方程:
①;
② .
22. 先化简 , 再从﹣1,1,3中选择一个适当的数作头x的值代入求值.23. 如图,△ABC的三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4). (1)、在图中作出△ABC关于y轴对称的△A1B1C1 , 并写出点A1、B1、C1的坐标(点A、B、C的对应点分别是点A1、B1、C1);(2)、在x轴上找一点P,使得PA+PB的距离最短,在图中作出点P的位置.24. 为了帮助湖北省武汉市防控新冠肺炎,某爱心组织筹集了部分资金,计划购买甲、乙两种救灾物资共2000件送往灾区,已知每件甲种物资的价格比每件乙种物资的价格贵10元,用350元购买甲种物资的件数恰好与用300元购买乙种物资的件数相同.(1)、求甲、乙两种救灾物资每件的价格各是多少元?(2)、经调查,灾区对甲种物资的需求量不少于乙种物资的1.5倍,该爱心组织共需要购买2000件物资,请问乙种物资最多能购买多少件?25. 综合与实践.
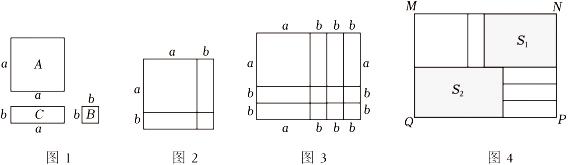
(1)、在图中作出△ABC关于y轴对称的△A1B1C1 , 并写出点A1、B1、C1的坐标(点A、B、C的对应点分别是点A1、B1、C1);(2)、在x轴上找一点P,使得PA+PB的距离最短,在图中作出点P的位置.24. 为了帮助湖北省武汉市防控新冠肺炎,某爱心组织筹集了部分资金,计划购买甲、乙两种救灾物资共2000件送往灾区,已知每件甲种物资的价格比每件乙种物资的价格贵10元,用350元购买甲种物资的件数恰好与用300元购买乙种物资的件数相同.(1)、求甲、乙两种救灾物资每件的价格各是多少元?(2)、经调查,灾区对甲种物资的需求量不少于乙种物资的1.5倍,该爱心组织共需要购买2000件物资,请问乙种物资最多能购买多少件?25. 综合与实践.学习整式乘法时,老师拿出三种型号的卡片,如图1,A型卡片是边长为a的正方形,B型卡片是边长为b的正方形,C型卡片是长和宽分别为a,b的长方形.
 (1)、选取1张A型卡片,2张C型卡片,1张B型卡片,在纸上按照图2的方式拼成一个边长为(a+b)的大正方形,通过用不同方式表示大正方形的面积,可得到乘法公式 .(2)、图3是由若干张A,B,C三种卡片拼成的一个长方形,观察图形,可将多项式a2+5ab+6b2分解因式为 .(3)、选取1张A型卡片,4张C型卡片按图4的方式不重叠地放在长方形MNPQ框架内,已知NP的长度固定不变,MN的长度可以变化,图中两阴影部分(长方形)的面积分别表示为S1 , S2 , 若Q=S1﹣S2 , 且Q为定值,则a与b有什么关系?请说明理由.26. 如图,等腰Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE.
(1)、选取1张A型卡片,2张C型卡片,1张B型卡片,在纸上按照图2的方式拼成一个边长为(a+b)的大正方形,通过用不同方式表示大正方形的面积,可得到乘法公式 .(2)、图3是由若干张A,B,C三种卡片拼成的一个长方形,观察图形,可将多项式a2+5ab+6b2分解因式为 .(3)、选取1张A型卡片,4张C型卡片按图4的方式不重叠地放在长方形MNPQ框架内,已知NP的长度固定不变,MN的长度可以变化,图中两阴影部分(长方形)的面积分别表示为S1 , S2 , 若Q=S1﹣S2 , 且Q为定值,则a与b有什么关系?请说明理由.26. 如图,等腰Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE. (1)、如图1,过F点作FG⊥AC交于G点,求证:AG=EC;(2)、如图2,连接BF交AC于G点,若AC=BC=4,AG=3,求证:E点为BC中点;(3)、如图3,当E点在CB的延长线上时,连接BF与AC的延长线交于D点,若 , 求的值是 .
(1)、如图1,过F点作FG⊥AC交于G点,求证:AG=EC;(2)、如图2,连接BF交AC于G点,若AC=BC=4,AG=3,求证:E点为BC中点;(3)、如图3,当E点在CB的延长线上时,连接BF与AC的延长线交于D点,若 , 求的值是 .