河北省石家庄市裕华区2023-2024学年七年级上学期期末数学试卷

试卷更新日期：2024-04-01 类型：期末考试

进入出卷网下载

一、选择题（本大题有16个小题，每小题2分，共32分.在每小题给出的四个题项中，只有一项是符合题目要求的）

1. 生产厂家检测4个足球的质量，结果如图所示，超过标准质量的克数记为正数，不足标准质量的克数记为负数，其中最标准的足球是（）

A、 B、 C、 D、

查看试题解析
2. 在一条沿直线l铺设的电缆两侧有P，Q两个小区，要求在直线l上的某处选取一点M，向P、Q两个小区铺设电缆，现有如下四种铺设方案，图中实线表示铺设的电缆，则所需电缆材料最短的是（）

A、 B、 C、 D、

查看试题解析
3. 下列各组数中，相等的一组是（）

A、﹣|﹣2|与﹣（﹣2） B、﹣2﹣3与﹣2÷ $\frac{2}{5}$ C、﹣3+7与﹣4 D、﹣5⁴与（﹣5）⁴

查看试题解析
4. 如图，点C在线段BD上，过A，B，C，D中的两点可以画一条直线，其中过点C的直线有（）

A、2条 B、3条 C、4条 D、5条

查看试题解析
5. 下列关于代数式的意义不正确的是（）

A、 $\frac{3 a}{2} + 4$ 表示a的3倍与4的和的一半 B、2（a+5）表示a与5的和的2倍 C、2a+5表示a的2倍与5的和 D、（a+b）²表示a与b的和的平方

查看试题解析
6. 在a﹣（2b﹣3c）=﹣□中的□内应填的代数式为（）

A、﹣a﹣2b+3c B、a﹣2b+3c C、﹣a+2b﹣3c D、a+2b﹣3c

查看试题解析
7. 小亮正确完成了以下两道作图题：①“延长线段AB到C，使BC＝AB“；②“反向延长线段DE到F，使点D是线段EF的一个三等分点”．针对小亮的作图，小莹说：“点B是线段AC中点”．小轩说：“DE＝2DF”．下列说法正确的是（）

A、小莹、小轩都对 B、小莹不对，小轩对 C、小莹、小轩都不对 D、小莹对，小轩不对

查看试题解析
8. 下列说法正确的是（）

A、﹣πab的次数为3 B、2a+ab﹣12是二次三项式 C、 $\frac{a b}{5}$ 的系数为5 D、﹣a³b和ab³同类项

查看试题解析
9. 下面是黑板上出示的尺规作图题，需要回答符号代表的内容（）
如图，已知∠AOB，求作：∠DEF，使∠DEF＝∠AOB
作法：
（1）以●为圆心，任意长为半径画弧，分别交OA、OB于点P、Q
（2）作射线EG，并以点E为圆心◎长为半径画弧交EG于点D
（3）以点D为圆心⊙长为半径画弧交（2）步中所画弧于点F
（4）作⊕，∠DEF即为所求作的角

A、●表示点E B、◎表示PQ C、⊙表示OQ D、⊕表示射线EF

查看试题解析
10. 在计算 $- 2^{2} + 5 \div (- 2) \times \frac{1}{2} - 9 \times (2 - \frac{1}{3} - \frac{2}{9})$ 时，有四位同学给出了以下四种计算步骤，其中正确的是（）

A、原式 $= 1 \div (- 2) \times \frac{1}{2} - 9 \times (2 - \frac{1}{3} - \frac{2}{9})$ B、原式 $= - 4 + 5 \div (- 1 - 9) \times (2 - \frac{1}{3} - \frac{2}{9})$ C、原式 $= - 4 + 5 \div (- 2) \times \frac{1}{2} - 18 + 3 + 2$ D、原式 $= 4 + 5 \div (- 2) \times \frac{1}{2} - 18 + 3 + 2$

查看试题解析
11. 如图，△ABC绕点P逆时针旋转一个角度得到△DEF，则下面选项中不能表示旋转角的是（）

A、∠CPD B、∠APD C、∠BPE D、∠CPF

查看试题解析
12. 下列等式变形中，正确的是（）

A、若3x﹣2＝5，则3x＝﹣7 B、若﹣8x＝4，则x＝﹣2 C、若 $- \frac{2}{3} x = 2$ ，则2x＝6 D、若5x+2＝﹣6，则5x＝﹣8

查看试题解析
13. 如图、用圆圈按照一定的规律拼图案，其中第（1）个图案有5个圆圈，第（2）个图案有8个圆圈，第（3）个图案有11个圆圈，…，按此规律拼下去，则第（7）个图案中圆圈的个数为（）

A、20 B、23 C、26 D、29

查看试题解析
14. 如图，将长方形纸片ABCD的角C沿着GF折叠（点F在BC上，不与B，C重合），使点C落在长方形内部点E处，若FH平分∠BFE，则∠GFH的度数α是（）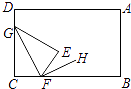

A、90°＜α＜180° B、0°＜α＜90° C、α=90° D、α随折痕GF位置的变化而变化

查看试题解析
15. 学校在一次研学活动中，有n位师生乘坐m辆客车，若每辆客车乘50人，则还有12人不能上车；若每辆客车乘55人，则最后一辆车空了8个座位．下列四个等式：①50m+12＝55m﹣8；
②50m+12＝55m+8；
③ $\frac{n - 12}{50} = \frac{n + 8}{55}$ ；
④ $\frac{n + 12}{50} = \frac{n - 8}{55}$ ．
其中正确的有（）

A、①③ B、①④ C、②③ D、②④

查看试题解析
16. 按下面的程序计算：
若输n＝100，输出结果是501；若输入n＝25，输出结果是631，若开始输入的n值为正整数，最后输出的结果为656，则开始输入的n值可能有（）

A、1种 B、2种 C、3种 D、4种

查看试题解析

二、填空题：（本大题有3个小题，17-18题每小题3分，19题每空2分，共10分.）

17. 已知x＝2是关于x的一元一次方程2x+k﹣1＝0的解，则k等于．

查看试题解析
18. 如图，∠AOC＝90°，OC平分∠DOB，∠DOC＝25°35'，∠BOA度数是

查看试题解析
19. 如图，线段AO、OB、BC三条线段首尾相接，组成折线段，AO＝OB＝10，BC＝7．动点P从点A出发，沿着A→O→B→C的方向运动，点P在AO上以2个单位长度/秒的速度运动，在OB上运动速度变为原来的一半，在BC上又恢复为2个单位长度/秒的速度运动；点P出发的同时，动点Q从点C出发，始终以1个单位长度/秒的速度沿着C→B→O→A的方向运动．当点P运动至点C时，点Q也随之停止运动．设运动的时间为t秒．

(1)、动点P从点A运动至点C需要秒；

(2)、当P，Q两点相遇时，相遇点M与点B相距个单位长度．

查看试题解析

三、解答题（本大题有7个小题，共58分.解答应写出文字说明、证明过程或演算步骤）

20. 在一条不完整的数轴上从左到右有A，B，C三点，其中AB＝2，BC＝1，如图所示，设点A，B，C所对应数的和是p．

(1)、若以C为原点，写出点A，B所对应的数，计算p的值；

(2)、若p的值是﹣1，求出点A，B，C所对应的数；

(3)、在（2）的条件下，在数轴上表示|﹣0.5|、（﹣1）³和A，B，C所对应的数，并把这5个数进行大小比较，用“＜”连接．

查看试题解析
21.

(1)、7+（﹣14）﹣（﹣9）﹣（+12）；

(2)、 $(- 3)^{2} \times | - \frac{2}{9} | - 8 \div (- 2)$ ；

(3)、（2a﹣b）﹣（2b﹣3a）﹣2（a﹣2b）；

(4)、 $\frac{x - 1}{2} - 1 = \frac{2 x + 2}{3}$ ；

(5)、（3a²+2a﹣1）﹣2（3﹣4a+2a²），其中a＝﹣2．

查看试题解析
22. 如图，一个长方形中剪下两个大小相同的正方形（有关线段的长如图所示，单位：米）留下一个“T”型图形（阴影部分）．

(1)、用含x，y的代数式表示“T”型图形的周长；

(2)、若此图作为某施工图，“T”型图形的周边需围上单价为每米20元的栅栏，原长方形周边的其余部分需围上单价为每米15元的栅栏．若x＝1，y＝3，请计算整个施工所需的造价．

查看试题解析
23. 若a+b＝1，则称a与b是关于1的平衡数．

(1)、6与是关于1的平衡数；

(2)、x﹣1与是关于1的平衡数；

(3)、若a＝2（3x²﹣x）﹣5，b＝x﹣（6x²﹣x﹣5），试判断a与b是否是关于1的平衡数，并说明理由．

查看试题解析
24. 如图，点 $E$ 是线段 $A B$ 的中点， $C$ 是 $E B$ 上一点，且 $E C ： C B = 1 ： 4$ ， $A C = 12 cm$

(1)、求 $A B$ 的长

(2)、若 $F$ 为 $C B$ 的中点，求 $E F$ 长

查看试题解析
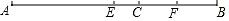25. 某玩具工厂出售一种玩具，其成本价为每件28元．如果直接由厂家门市销售，每件产品售价为35元，同时每月还要支出其他费用2100元；如果委托商场销售，那么出厂价为每件32元．

(1)、若用x表示每月销售该种玩具的件数，请你用含x的式子分别表示这两种销售方式所得的利润．

(2)、在两种销售方式下，每个月销售多少件时，所得利润相等？

(3)、若每个月的销售量为1000件时，采用哪种销售方式获得利润较多？其利润是多少？

查看试题解析
26. 如图，O为直线MN上一点，将一副直角三角尺（分别含45°、45°、90°和30°、60°、90°的角）按图中方式放在点O处，使∠AOC＝150°．将三角尺AOB绕点O以每秒5°的速度顺时针旋转，旋转180°后停止设运动时间为t秒．

(1)、当t＝5时，∠BOC＝°；

(2)、若在三角尺AOB开始旋转的同时，三角尺COD也绕点O以每秒10°的速度逆时针旋转，当三角尺AOB停止旋转时，三角尺COD也停止旋转．
①在线段OA与OC第一次相遇前，t为何值时，OA平分∠COD；
②在旋转过程中，是否存在某一时刻使∠AOD＝2∠BOC．若存在，请求出t的值；若不存在，请说明理由．

查看试题解析