湖南省长沙市师大附中集团2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-04-01 类型:期末考试
一、选择题(本大题10个小题,每小题3分,共30分)
-
1. 已知反比例函数的图象经过点 , 则k的值为( )A、3 B、4 C、5 D、62. 若 , 则( )A、 B、 C、 D、3. 下列语句中正确的是( )A、平分弦的直径垂直于弦 B、三点确定一个圆 C、三角形的内心到三角形三边的距离相等 D、各边相等的多边形是正多边形4. 某几何体如图所示,则从正面观察这个图形,得到的平面图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,直线a∥b∥c , 分别交直线m、n于点A、C、E、B、D、F , 下列结论正确的是( )
5. 如图,直线a∥b∥c , 分别交直线m、n于点A、C、E、B、D、F , 下列结论正确的是( ) A、 B、 C、 D、6. 如图,与位似,位似中心是点 , 且 , 若的面积为5,则的面积为( )
A、 B、 C、 D、6. 如图,与位似,位似中心是点 , 且 , 若的面积为5,则的面积为( ) A、10 B、15 C、20 D、257. 不透明的袋子中只有2个黑球和4个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是不可能事件的是( )A、3个球都是黑球 B、3个球都是白球 C、三个球中有黑球 D、3个球中有白球8. 在直角△ABC中,∠C=90°,BC=3,sinA= , 求tanB为( )A、 B、 C、 D、9. 若关于x的函数y=x2+bx+3与x轴有两个不同的交点,则b的值不可能是( )A、4 B、﹣3 C、5 D、﹣610. 如图,在正方形ABCD中,点E在边CD上,点H在边AD上,CE=DH , CH交BE于点F , 交BD于点G , 连接GE . 下列结论:①CH=BE;②CH⊥BE;③S△GCE=S△GDH;④当E是CD的中点时,;⑤当EC=2DE时,S正方形ABCD=6S四边形DEGH . 其中正确结论的序号是( )
A、10 B、15 C、20 D、257. 不透明的袋子中只有2个黑球和4个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是不可能事件的是( )A、3个球都是黑球 B、3个球都是白球 C、三个球中有黑球 D、3个球中有白球8. 在直角△ABC中,∠C=90°,BC=3,sinA= , 求tanB为( )A、 B、 C、 D、9. 若关于x的函数y=x2+bx+3与x轴有两个不同的交点,则b的值不可能是( )A、4 B、﹣3 C、5 D、﹣610. 如图,在正方形ABCD中,点E在边CD上,点H在边AD上,CE=DH , CH交BE于点F , 交BD于点G , 连接GE . 下列结论:①CH=BE;②CH⊥BE;③S△GCE=S△GDH;④当E是CD的中点时,;⑤当EC=2DE时,S正方形ABCD=6S四边形DEGH . 其中正确结论的序号是( ) A、①②③④ B、①②③⑤ C、①③④⑤ D、②④⑤
A、①②③④ B、①②③⑤ C、①③④⑤ D、②④⑤二、填空题(共6小题,每小题3分,共18分)
-
11. 若点A(﹣2,5),与点B关于原点对称,则点B的坐标为 .12. 时钟的分针长6厘米,从上午8:10到上午8:30,分针扫过的面积是平方厘米.13. 二次函数y=x2﹣2x+2的最小值是 .14. 如图,M为反比例函数的图象上的一点,MA⊥y轴,垂足为A , △AOM的面积为3,则k的值为 .
 15. 如图,PA、PB分别切⊙O于A、B , PA=10cm , C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交PA、PB于点E、F . 则△PEF的周长为cm .
15. 如图,PA、PB分别切⊙O于A、B , PA=10cm , C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交PA、PB于点E、F . 则△PEF的周长为cm . 16. 《九章算术》是我国数学经典,上面记载:“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方几何?”其意思是:如图,已知正方形小城ABCD , 点E , G分别为CD , AD的中点,EF⊥CD , GH⊥AD , 点F , D , H在一条直线上,EF=30步,GH=750步.问正方形小城ABCD的边长是多少?该问题的答案是 .
16. 《九章算术》是我国数学经典,上面记载:“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方几何?”其意思是:如图,已知正方形小城ABCD , 点E , G分别为CD , AD的中点,EF⊥CD , GH⊥AD , 点F , D , H在一条直线上,EF=30步,GH=750步.问正方形小城ABCD的边长是多少?该问题的答案是 .
三、解答题(共9小题,其中17、18、19每小题6分,20、21每小题8分,22、23每小题9分,24、25每小题10分,共72分)
-
17. 计算: .18. 先化简 , 然后再从x=0,﹣1,1,中选择一个合适的值代入求值.19. 如图,扶梯AB的坡度为4:3,滑梯CD的坡度为1:2.设AE=30dm , BC=50dm , 一女孩从扶梯走到滑梯的顶部,然后从滑梯滑下,她经过的总路程是多少(结果保留根号)?
 20. 科学实验是获取经验事实和检验科学假说、理论真理性的重要途径.某校为进一步培养学生实践创新能力,提高学生科学素养,营造爱科学、学科学、用科学的浓厚氛围,将开展“崇尚科学科技月”主题教育活动,计划演示以下四项科学小实验:A . 自动升高的水;B . 不会湿的纸;C . 漂浮的硬币;D . 生气的瓶子.学校科技部随机对该校部分学生进行了“最希望演示的一项实验”问卷调查,得到下列不完整的统计图.请结合统计图,回答下列问题:
20. 科学实验是获取经验事实和检验科学假说、理论真理性的重要途径.某校为进一步培养学生实践创新能力,提高学生科学素养,营造爱科学、学科学、用科学的浓厚氛围,将开展“崇尚科学科技月”主题教育活动,计划演示以下四项科学小实验:A . 自动升高的水;B . 不会湿的纸;C . 漂浮的硬币;D . 生气的瓶子.学校科技部随机对该校部分学生进行了“最希望演示的一项实验”问卷调查,得到下列不完整的统计图.请结合统计图,回答下列问题: (1)、求此次调查中接受调查的人数;(2)、请补全条形统计图;(3)、已知最希望演示A项实验的4名学生,有1名来自九年级一班,1名来自九年级二班,2名来自九年级三班,现需从这四人中随机抽取2名作为实验“自动升高的水”的演示员,请用列表或画树状图的方法,求抽到的2名学生来自不同班级的概率.21. 如图①是某款智能磁吸键盘,如图②是平板吸附在该款设备上的照片,图③是图②的示意图.已知BC=8cm , CD=20cm , ∠BCD=63°.当AE与BC形成的∠ABC为116°时,求DE的长.(参考数据:sin63°≈0.90,cos63°≈0.45,cot63°≈0.50;sin53°≈0.80,cos53°≈0.60,cot53°≈0.75)
(1)、求此次调查中接受调查的人数;(2)、请补全条形统计图;(3)、已知最希望演示A项实验的4名学生,有1名来自九年级一班,1名来自九年级二班,2名来自九年级三班,现需从这四人中随机抽取2名作为实验“自动升高的水”的演示员,请用列表或画树状图的方法,求抽到的2名学生来自不同班级的概率.21. 如图①是某款智能磁吸键盘,如图②是平板吸附在该款设备上的照片,图③是图②的示意图.已知BC=8cm , CD=20cm , ∠BCD=63°.当AE与BC形成的∠ABC为116°时,求DE的长.(参考数据:sin63°≈0.90,cos63°≈0.45,cot63°≈0.50;sin53°≈0.80,cos53°≈0.60,cot53°≈0.75) 22. 如图,在⊙O中,BC为非直径弦,点D是的中点,CD是△ABC的角平分线.
22. 如图,在⊙O中,BC为非直径弦,点D是的中点,CD是△ABC的角平分线. (1)、求证:∠ACD=∠ABC;(2)、求证:AC是⊙O的切线;(3)、若BD=1,时,求弦BD与围城的弓形面积.23. 一透明的敞口正方体容器ABCD﹣A'B'C'D'装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α,如图所示).
(1)、求证:∠ACD=∠ABC;(2)、求证:AC是⊙O的切线;(3)、若BD=1,时,求弦BD与围城的弓形面积.23. 一透明的敞口正方体容器ABCD﹣A'B'C'D'装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α,如图所示).

探究:如图1,液面刚好过棱CD , 并与棱BB'交于点Q , 此时液体的形状为直三棱柱,其三视图及尺寸如图②.
(1)、解决问题:CQ与BE的位置关系是 , BQ的长是dm , α=°(注:sin49°=cos41° , tan37°)(2)、求液体的体积;(参考算法:直棱柱体积V液=底面积SBCQ×高AB)(3)、在图1的基础上,以棱AB为轴将容器向左或向右旋转,但不能使液体溢出.图3或图4是其正面示意图,若液面与棱C'C或CB交于点P、点Q始终在棱BB'上,设PC=x , BQ=y , 分别就图3和图4求y与x的函数关系式,并写出相应的α的范围.24. 如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P , Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ . 点D , E分别是点A , B以Q , P为对称中心的对称点,HQ⊥AB于Q , 交AC于点H . 当点E到达顶点A时,P , Q同时停止运动.设BP的长为x , △HDE的面积为y . (1)、求证:△DHQ∽△ABC;(2)、求y关于x的函数解析式并求y的最大值;(3)、当x为何值时,△HDE为等腰三角形?25. 若凸四边形的两条对角线所夹锐角为60°,我们称这样的凸四边形为“美丽四边形”.
(1)、求证:△DHQ∽△ABC;(2)、求y关于x的函数解析式并求y的最大值;(3)、当x为何值时,△HDE为等腰三角形?25. 若凸四边形的两条对角线所夹锐角为60°,我们称这样的凸四边形为“美丽四边形”.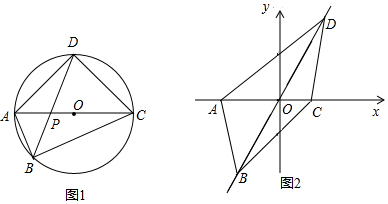 (1)、①在“平行四边形、梯形、菱形、正方形”中,一定不是“美丽四边形”的有 ;
(1)、①在“平行四边形、梯形、菱形、正方形”中,一定不是“美丽四边形”的有 ;②若矩形ABCD是“美丽四边形”,且AB=3,则BC=;
(2)、如图1,“美丽四边形”ABCD内接于⊙O , AC与BD相交于点P , 且对角线AC为直径,AP=1,PC=5,求另一条对角线BD的长;(3)、如图2,平面直角坐标系中,已知“美丽四边形”ABCD的四个顶点A(﹣3,0)、C(2,0),B在第三象限,D在第一象限,AC与BD交于点O , 且四边形ABCD的面积为 , 若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.