河北省保定市阜平县2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-04-01 类型：期末考试

进入出卷网下载

一、单选题

1. “我爱中国”这四个汉字拼音的首字母如下，其中属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 建设中的G107马头南至冀豫界段是我省“十四五”建设项目，其某段施工需运送土石方 $1 0^{4} m^{3}$ ，则土石方日运送量 $V (m^{3} / 天)$ 与完成运送任务所需时间 $t$ （天）满足（）

A、反比例函数关系 B、正比例函数关系 C、一次函数关系 D、二次函数关系

查看试题解析
3. 如图，在Rt△ABC中，∠C＝90°，则sinB的值是（）

A、 $\frac{B C}{A B}$ B、 $\frac{A B}{A C}$ C、 $\frac{A C}{A B}$ D、 $\frac{A C}{B C}$

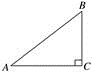查看试题解析
4. 将抛物线y＝x²向右平移1个单位长度，得到的抛物线的解析式为（）

A、y＝x²－1 B、y＝x²＋1 C、y＝（x＋1）² D、y＝（x－1）²

查看试题解析
5. 已知事件①：任意画一个多边形，其外角和为 $360 °$ ；事件②：明天下雨，下列说法正确的是（）

A、事件①和②都是随机事件 B、事件①和②都是必然事件 C、事件①是随机事件，事件②是必然事件 D、事件①是必然事件，事件②是随机事件

查看试题解析
6. 如图， $△ O A_{1} B_{1}$ 与 $△ O A B$ 的形状相同，大小不同， $△ O A_{1} B_{1}$ 是由 $△ O A B$ 的各顶点变化得到的，则各顶点变化情况是（）

A、横坐标和纵坐标都乘以2 B、横坐标和纵坐标都加2 C、横坐标和纵坐标都除以2 D、横坐标和纵坐标都减2

查看试题解析
7. 如图，在 $⊙ O$ 中，点C在 $\overset{⌢}{A D}$ 上．若 $\overset{⌢}{A B} = \overset{⌢}{B D}$ ， $∠ A O B = 110 °$ ，则 $∠ B C D$ 的度数为（）

A、 $110 °$ B、 $70 °$ C、 $55 °$ D、 $50 °$

查看试题解析
8. 如图，将 $△ A B C$ 绕点C顺时针旋转，点B的对应点为点E ，点A的对应点为点D ，当点E恰好落在 $A C$ 边上时，连接 $A D$ ，若 $∠ A C B = 30 °$ ，则 $∠ D A C$ 的度数是（）

A、 $60 °$ B、 $65 °$ C、 $70 °$ D、 $75 °$

查看试题解析
9. 2021年以来，某厂生产的电子产品处于高速增长上升期，该厂生产一件产品起初的成本为125元，经过两次技术改进，现生产一件这种产品的成本比起初下降了19.2元.设每次技术改进时，产品的成本下降率均为 $x$ ，则下列方程正确的是（）

A、 $125 (1 - 2 x) = 125 - 19.2$ B、 $19.2 (1 + x)^{2} = 125$ C、 ${(1 - x)}^{2} = 19.2$ D、 $125 (1 - x)^{2} = 125 - 19.2$

查看试题解析
10. 若关于x的方程 $x^{2} - m x + 9 = 0$ 有两个相等的实数根，则实数m的值为（）

A、6 B、 $- 6$ C、9 D、6或 $- 6$

查看试题解析
11. 一个乒乓球从光滑斜面自由滚下的路程y（米）与时间x（秒）的平方成正比例，当乒乓球滚下3米时，经过的时间为1.5秒，当 $x = 2$ 时，该乒乓球所经过的路程为（）

A、5米 B、 $\frac{16}{3}$ 米 C、 $\frac{8}{3}$ 米 D、 $\frac{2}{3}$ 米

查看试题解析
12. 已知二次函数 $y = x^{2} + b x + c$ 的图象如图所示，则一次函数 $y = b x + c$ 与反比例函数 $y = \frac{b c}{x}$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
13. 如图是一个钟表表盘，连接整点2时与整点10时的B ， D两点并延长，交过整点8时的切线于点 $P$ ，若表盘的半径长为 $\sqrt{3}$ ，则切线长 $P C$ 为（）

A、3 B、2 C、 $2 \sqrt{3}$ D、 $3 \sqrt{3}$

查看试题解析
14. 如图是由8个小正方形组成的网格，则在 $△ A B D$ ， $△ A C D$ ， $△ E B D$ ， $△ E A F$ 中，与 $△ A B C$ 相似的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
15. 如图，等腰直角三角形 $A B C$ 在第一象限，点A ， B的坐标分别为 $(1 ， 5) ， (1 ， 2)$ ， $∠ B = 90 °$ ．动点D从点A出发，沿 $A B - B C$ 运动到点C ，反比例函数 $y = \frac{k}{x}$ （ $x > 0$ ）的图象L经过点D ，则在点D的运动过程中，下列各点中，图象L经过两次的是（）

A、 $(1 ， 2)$ B、 $(3 ， 2)$ C、 $(2 ， 2)$ D、 $(4 ， 2)$

查看试题解析
16. 如图，正六边形 $A B C D E F$ 内接于 $⊙ O$ ，点P在边 $B C$ 上．结论Ⅰ：若 $⊙ O$ 的半径为2，P是边 $B C$ 的中点，则 $P E$ 的长为 $\sqrt{13}$ ；结论Ⅱ：连接 $P F$ ．若 $S_{△ P E F} = \frac{\sqrt{3}}{2}$ ，则 $\overset{⌢}{E F}$ 的长为 $\frac{π}{3}$ ，关于结论Ⅰ、Ⅱ，判断正确的是（）

A、只有结论Ⅰ对 B、只有结论Ⅱ对 C、结论Ⅰ、Ⅱ都对 D、结论Ⅰ、Ⅱ都不对

查看试题解析

二、填空题

17. 已知反比例函数 $y = \frac{k}{x}$ ，若当 $x < 0$ 时 $y$ 随 $x$ 的增大而增大，写出一个符合条件的 $k$ 的整数值：.

查看试题解析
18. 如图，在 $△ A B C$ 中， $D$ ， $F$ 是 $A B$ 的三等分点， $D E ∥ F G ∥ B C$ .

(1)、若 $D E = 2$ ，则 $B C =$ ；

(2)、 $S_{△ A D E} ： S_{△ A F G} ： S_{△ A B C} =$ .

查看试题解析
19. 已知函数 $y = {(x - 2)}^{2} + m$ ．

(1)、若 $m = 1$ ，则该函数图象与y轴的交点坐标为；

(2)、当 $x \leq m$ 时，函数 $y = {(x - 2)}^{2} + m$ 的最小值为4，则m的值为．

查看试题解析

三、解答题

20. 解下列方程．

(1)、 $x^{2} - 4 x = 12$ ；

(2)、 $2 x^{2} - 7 x + 3 = 0$ ．

查看试题解析
21. 如图1、图2， $△ A B O$ 的顶点都在平面直角坐标系中的网格点上．

(1)、在图1中画出与 $△ A B O$ 关于点O对称的 $△ A^{'} B^{'} O$ ，点 $A^{'}$ 的坐标为 ▲ ；

(2)、在图2的网格中找一格点C ，使得以A ， B ， O ， C为顶点的四边形是中心对称图形．

查看试题解析
22. 如图，已知点 $B (4 ， 4)$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过点 $A (1 ， 3)$ ．

(1)、求反比例函数的解析式，并在图中画出该反比例函数的图象；

(2)、当 $x ≥ 3$ 时，求函数值y的取值范围；

(3)、若关于x的一次函数 $y = a x + b (a \neq 0)$ 的图象经过点B ，且与图中的反比例函数的图象交于点P ，当 $a > 0$ 时，直接写出点P的横坐标 $x_{P}$ 的取值范围．

查看试题解析
23. 现有四张不透明且质地相同的数字卡片，卡片正面分别写有数字1，1，3，4，将卡片洗匀后，背面朝上放置在桌面上．

(1)、随机抽取一张卡片，恰好得到数字1的概率为；

(2)、班级图书角新加一本《西游记》，嘉嘉和淇淇都想看，张红用以上四张卡片设计了游戏：随机抽取一张卡片，记下数字后不放回，再从剩余的卡片中随机抽取一张记下数字，将抽取的第一张、第二张卡片上的数字相加．若两数之和为奇数，则嘉嘉先看；若两数之和为偶数，则淇淇先看，但嘉嘉却认为这个游戏设计得不公平，请你画树状图求出嘉嘉先看《西游记》的概率，再判断嘉嘉的说法是否正确．

查看试题解析
24. 小明对他击羽毛球的路线进行分析．如图，在平面直角坐标系中，点A ， C在x轴上，球网 $A B$ 与y轴的水平距离 $O A = 3 m$ ， $C A = 2 m$ ，击球点P在y轴上．若小明选择扣球，羽毛球的飞行高度 $y (m)$ 与水平距离 $x (m)$ 近似满足一次函数关系 $y = - 0.4 x + 2.8$ ；若小明选择吊球，羽毛球的飞行高度 $y (m)$ 与水平距离 $x (m)$ 近似满足二次函数关系 $y = a {(x - 1)}^{2} + 3.2$ ．

(1)、求点P的坐标和a的值；

(2)、通过分析发现，上面两种击球方式均能使球过球网 $A B$ ．要使球的落地点到点C的距离更近，请通过计算判断应选择哪种击球方式；

(3)、小明在点P处再次以吊球的方式击球，此次羽毛球飞行路线的形状与 $y = a {(x - 1)}^{2} + 3.2$ 的相同，且恰好落到点C处，则此次羽毛球飞行到最高点时与y轴的水平距离比 $1 m$ （填“大”或“小”）．

查看试题解析
25. 如图1，将 $R t △ A B C$ 的顶点C放在 $⊙ O$ 上，边 $B C$ 与 $⊙ O$ 相切于点C ，边 $A C$ 与 $⊙ O$ 交于点D ．已知 $∠ B C A = 60 °$ ， $∠ B = 90 °$ ， $B C = 6$ ， $⊙ O$ 的直径为8．

(1)、如图1，过点O作 $O M ⊥ C D$ 于点M ，求 $C M$ 的长度；

(2)、从图1的位置开始，将 $△ A B C$ 绕点C顺时针旋转，设旋转角为 $α$ （ $0 ° \leq α \leq 360 °$ ）．
①如图2，当 $α = 20 °$ 时，边 $B C$ 与 $⊙ O$ 的另一交点为E ，求 $\overset{⌢}{C E}$ 的长度；
②如图3，当 $A C$ 经过圆心O时，试判断 $A B$ 与 $⊙ O$ 之间的位置关系，并说明理由；
③在旋转过程中，直接写出点O到边 $A B$ 的距离h的取值范围．

查看试题解析
26. 在 $△ A B C$ 中， $∠ A B C = 9 0^{∘}$ ， $A B = 3$ ， $B C = 4$ .点 $Q$ 在线段 $A C$ 上运动，过点 $Q$ 作 $A C$ 的垂线交线段 $A B$ （如图1）或线段 $A B$ 的延长线（如图2）于点 $P$ ．

图1 图2 备用图

(1)、当点 $P$ 在线段 $A B$ 上时，求证： $△ A Q P ∽ △ A B C$ ；

(2)、当点 $P$ 与点 $B$ 重合时，求 $A Q$ 的长；

(3)、若点 $Q$ 从点 $A$ 以每秒2个单位长的速度向点 $C$ 运动，求点 $P$ 与点 $B$ 的距离不大于1的时长；

(4)、当 $△ B P Q$ 为等腰三角形时，直接写出 $A P$ 的长．

查看试题解析