河北省石家庄市平山县2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-04-01 类型:期末考试
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 下列图标中,既是轴对称图形又是中心对称图形是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列方程是关于x的一元二次方程的是.( )A、 B、 C、 D、3. 下列事件是随机事件的是( )A、三角形内角和为360度 B、测量某天的最低气温,结果为 C、买一张彩票,中奖 D、太阳从东方升起4. 若点M在抛物线的对称轴上,则点M的坐标可能是( )A、 B、 C、 D、5. 已知,的半径 , 若 , 则直线与位置图形可能为( )A、
2. 下列方程是关于x的一元二次方程的是.( )A、 B、 C、 D、3. 下列事件是随机事件的是( )A、三角形内角和为360度 B、测量某天的最低气温,结果为 C、买一张彩票,中奖 D、太阳从东方升起4. 若点M在抛物线的对称轴上,则点M的坐标可能是( )A、 B、 C、 D、5. 已知,的半径 , 若 , 则直线与位置图形可能为( )A、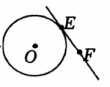 B、
B、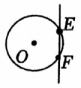 C、
C、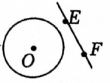 D、
D、 6. 点在函数图象上,下列说法中错误的是( )A、它的图象分布在二、四象限 B、当时,y的值随x的增大而增大 C、当时,y的值随x的增大而减小 D、它的图象过点7. 如图,在平面直角坐标系中,已知点A,B的坐标分别为 , . 以点O为位似中心,在原点的另一侧按2:1的相似比将缩小,则点A的对应点的坐标是( )
6. 点在函数图象上,下列说法中错误的是( )A、它的图象分布在二、四象限 B、当时,y的值随x的增大而增大 C、当时,y的值随x的增大而减小 D、它的图象过点7. 如图,在平面直角坐标系中,已知点A,B的坐标分别为 , . 以点O为位似中心,在原点的另一侧按2:1的相似比将缩小,则点A的对应点的坐标是( ) A、 B、 C、 D、8. 若点与点关于原点对称,则的值为( )A、1 B、4 C、 D、9. 如图,在中, , , 将绕点C顺时针旋转90°得到 , 点B的对应点B在边上(不与点A,C重合),则的度数为( )
A、 B、 C、 D、8. 若点与点关于原点对称,则的值为( )A、1 B、4 C、 D、9. 如图,在中, , , 将绕点C顺时针旋转90°得到 , 点B的对应点B在边上(不与点A,C重合),则的度数为( ) A、α B、 C、 D、10. 10月8日,杭州亚运会乒乓球比赛全部结束,国乒揽获除女双项目外的6块金牌,展现了在乒乓球领域强大的统治力.乒乓球比赛采用双循环制(每两队之间都进行两场比赛),比赛总场数为380场,若设参赛队伍有x支,则可列方程为( )A、 B、 C、 D、11. 如图,点A在反比例函数的图象上,过点A分别作x轴的垂线,垂足为B,若的面积为1,则k的值为( )
A、α B、 C、 D、10. 10月8日,杭州亚运会乒乓球比赛全部结束,国乒揽获除女双项目外的6块金牌,展现了在乒乓球领域强大的统治力.乒乓球比赛采用双循环制(每两队之间都进行两场比赛),比赛总场数为380场,若设参赛队伍有x支,则可列方程为( )A、 B、 C、 D、11. 如图,点A在反比例函数的图象上,过点A分别作x轴的垂线,垂足为B,若的面积为1,则k的值为( ) A、2 B、1 C、 D、12. 如图,点A、点B、点C均在上,是直径且 , , 则的长为( )
A、2 B、1 C、 D、12. 如图,点A、点B、点C均在上,是直径且 , , 则的长为( ) A、 B、1 C、 D、13. 已知二次函数的图象如图所示,则一次函数的图象和反比例函数的图象在同一坐标系中大致为( )
A、 B、1 C、 D、13. 已知二次函数的图象如图所示,则一次函数的图象和反比例函数的图象在同一坐标系中大致为( ) A、
A、 B、
B、 C、
C、 D、
D、 14. 如图,抛物线与x轴交于C、D两点(点C在点D的左侧),顶点在线段上运动,轴, , , 则下列结论中正确的是( )
14. 如图,抛物线与x轴交于C、D两点(点C在点D的左侧),顶点在线段上运动,轴, , , 则下列结论中正确的是( ) A、 B、当时,一定有y随x的增大而增大 C、 D、若点C的坐标为 , 则点D的坐标为15. 如图,在平面直角坐标系中,经过点 , 直线与交于B、C两点,则弦的最小值是( )
A、 B、当时,一定有y随x的增大而增大 C、 D、若点C的坐标为 , 则点D的坐标为15. 如图,在平面直角坐标系中,经过点 , 直线与交于B、C两点,则弦的最小值是( ) A、 B、 C、 D、以上都不对16. 如图,二次函数及一次函数 , 将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数,当直线与新图象有4个交点时,m的取值范围是( )
A、 B、 C、 D、以上都不对16. 如图,二次函数及一次函数 , 将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数,当直线与新图象有4个交点时,m的取值范围是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共3个小题,共10分.其中17、18小题每小题3分,19小题每空2分)
-
17. 在不透明袋子里装有颜色不同的8个球,这些球除颜色外完全相同.每次从袋子里摸出1个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.25,估计袋中白球有个.18. 如图,的三个顶点都在的网格(每个小正方形的边长均为1个单位长度)的格点上,将绕点B逆时针旋转到的位置,且点、仍落在格点上,则图中阴影部分的面积约是 . (保留π)
 19. 如图,M是斜边上的中点,将绕点B旋转,A使得点C落在射线上的点D处,点A落在点E处,边的延长线交边于点F.如果 . . 那么的长为;的长为 .
19. 如图,M是斜边上的中点,将绕点B旋转,A使得点C落在射线上的点D处,点A落在点E处,边的延长线交边于点F.如果 . . 那么的长为;的长为 .
三、解答题(本大题7个小题,共68分.解答应写出文字说明、证明过程或演算步骤)
-
20. 解方程:(1)、(2)、21. 嘉嘉在学完物理“电学”知识后,进行“灯泡亮了”的实验,设计了如图所示的电路图,电路图上有5个开关、、、、和一个小灯泡,当开关闭合时,再同时闭合开关、或、都可以使小灯泡发亮.
 (1)、当开关、已经闭合时,再任意闭合开关、、中的一个,小灯泡能亮起来的概率是;(2)、当开关已经闭合时,再任意闭合开关、、、中的两个,请用列表或画树状图的方法求小灯泡能亮起来的概率.22. 如图,在△ABC和△ADE中,已知∠B=∠D,∠BAD=∠CAE.
(1)、当开关、已经闭合时,再任意闭合开关、、中的一个,小灯泡能亮起来的概率是;(2)、当开关已经闭合时,再任意闭合开关、、、中的两个,请用列表或画树状图的方法求小灯泡能亮起来的概率.22. 如图,在△ABC和△ADE中,已知∠B=∠D,∠BAD=∠CAE.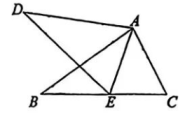 (1)、求证:△ABC∽△ADE.(2)、若S△ABC:S△ADE=4:9,BC=6,求DE的长.23. 如图,是的直径, , , 相交于点E,过点C作 , 与的延长线相交于点F,连接 .
(1)、求证:△ABC∽△ADE.(2)、若S△ABC:S△ADE=4:9,BC=6,求DE的长.23. 如图,是的直径, , , 相交于点E,过点C作 , 与的延长线相交于点F,连接 . (1)、求证:是的切线;(2)、若 , , 求的长.24. 某公司生产的某种商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:
(1)、求证:是的切线;(2)、若 , , 求的长.24. 某公司生产的某种商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:时间t(天)
1
3
5
10
36
…
日销售量m(件)
94
90
86
76
24
…
未来40天内,前20天每天的价格(元/件)与时间t(天)的函数关系式为(且t为整数),后20天每天的价格(元/件)与时间t(天)的函数关系式为(且为整数).
下面我们就来研究销售这种商品的有关问题:
(1)、认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的表达式;(2)、请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?25. 如图,在平面直角坐标系中,已知四边形是矩形,且 , , . 反比例函数的图象分别交、于点E、点F. (1)、求反比例函数的解析式;(2)、连接、、 , 求的面积;(3)、是否存在x轴上的一点P,使得是不以点P为直角顶点的直角三角形?若存在,请直接写出符合题意的点P的坐标;若不存在,请说明理由.26. 如图1,已知抛物线与x轴交于点和点 , 与y轴交于点C.
(1)、求反比例函数的解析式;(2)、连接、、 , 求的面积;(3)、是否存在x轴上的一点P,使得是不以点P为直角顶点的直角三角形?若存在,请直接写出符合题意的点P的坐标;若不存在,请说明理由.26. 如图1,已知抛物线与x轴交于点和点 , 与y轴交于点C.图1
 图2
图2  图3
图3 (1)、求b和c的值;(2)、已知点D是在第一象限内的抛物线上的一点,过点D作轴于点E.
(1)、求b和c的值;(2)、已知点D是在第一象限内的抛物线上的一点,过点D作轴于点E.①如图2,点D是抛物线的顶点,点P是上一点,若 , 求点P的坐标;
②如图3,若与交于点F,连接 , 且 , 求点D的坐标.