河北省石家庄重点中学2023-2024学年八年级上学期期末数学试卷

试卷更新日期：2024-04-01 类型：期末考试

进入出卷网下载

一、选择题：本题共16小题，共42分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 下列各数中，无理数的是（）

A、 $\sqrt{6}$ B、 $\sqrt{25}$ C、 $\frac{7}{13}$ D、3.1415

查看试题解析
2. 若 $\frac{\sqrt{x + 2}}{x}$ 有意义，则实数 $x$ 的取值范围为（）

A、 $x > - 2$ B、 $x \geq - 2$ C、 $x > - 2$ 且 $x \neq 0$ D、 $x \geq - 2$ 且 $x \neq 0$

查看试题解析
3. 等腰三角形的两边长分别是 $2$ ， $4$ ，则第三边长为（）

A、 $2$ B、 $4$ C、 $2$ 或 $4$ D、 $3$ 或 $4$

查看试题解析
4. 下列式子为最简二次根式的是（）

A、 $\sqrt{14}$ B、 $\sqrt{12}$ C、 $\sqrt{4}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
5. 如图，BE＝CF，AE⊥BC，DF⊥BC，要根据“HL”证明Rt△ABE≌Rt△DCF，则还要添加一个条件是（）

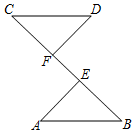A、AB＝DC B、∠A＝∠D C、∠B＝∠C D、AE＝BF

查看试题解析
6. 围棋起源于中国，古代称之为“弈”，至今已有 $4000$ 多年的历史 $.$ 以下是在棋谱中截取的四个部分，由黑白棋子摆成的图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
7. 估计 $\sqrt{5} + 2$ 的值在（）

A、 $2$ 和 $3$ 之间 B、 $3$ 和 $4$ 之间 C、 $4$ 和 $5$ 之间 D、 $5$ 和 $6$ 之间

查看试题解析
8. 化简分式 $\frac{7 a + 7 b}{（ a + b ）^{2}}$ 的结果是（）

A、 $\frac{a + b}{7}$ B、 $\frac{7}{a + b}$ C、 $\frac{a - b}{7}$ D、 $\frac{7}{a - b}$

查看试题解析
9. 矩形相邻两边长分别为 $\sqrt{2}$ ， $\sqrt{8}$ ，则它的周长和面积分别是（　　）

A、 $\sqrt{10}$ ， 4 B、2 $\sqrt{10}$ ， 4 C、4，3 $\sqrt{2}$ D、6 $\sqrt{2}$ ， 4

查看试题解析
10. $A D$ 是 $R t △ A B C$ 的角平分线，若 $A B = 4$ ， $B D = 3$ ，则点 $D$ 到 $A C$ 距离为（）

A、 $3$ B、 $4$ C、 $5$ D、 $6$

查看试题解析
11. 如图，在 $R t △ A B C$ 中， $∠ B = 90 ° ， ∠ A = 40 °$ ，AC的垂直平分线MN与AB交于点D，则 $∠ B C D$ 的度数是（）

A、10° B、15° C、20° D、25°

查看试题解析
12. 如图，若 $△ A B C$ ≌ $△ A D E$ ，则下列结论中不成立的是（）

A、 $∠ B A D = ∠ C A E$ B、 $∠ B A D = ∠ C D E$ C、 $D A$ 平分 $∠ B D E$ D、 $A C = D E$

查看试题解析
13. 下列命题正确的是（）

A、两边及一角对应相等的两个三角形全等 B、将 $32000$ 精确到千位，记为 $3.20 \times 10^{4}$ C、 $16$ 的平方根是 $4$ D、到三角形三个顶点距离相等的点在这个三角形三边的垂直平分线上

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = 3$ ， $A C = 4$ ， $B C = 5$ ， $E F$ 垂直平分 $B C$ ，点P为直线 $E F$ 上的任一点，则 $A P + B P$ 的最小值是（）

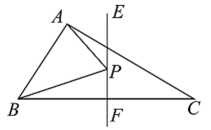A、3 B、4 C、5 D、6

查看试题解析
15. 在以下三个图形中，根据尺规作图的痕迹，能判断射线AD平分∠BAC的是（）

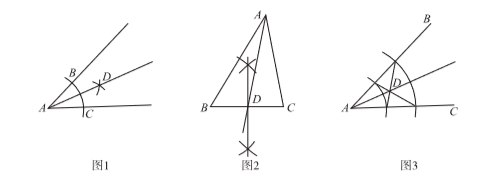A、图2 B、图1与图2 C、图1与图3 D、图2与图3

查看试题解析
16. 如图，已知 $△ A B C$ 与 $△ C D A$ 关于点 $O$ 对称，过点 $O$ 任作直线 $E F$ 分别交 $A D$ 、 $B C$ 于点 $M$ 、 $N$ ，下列结论：
$（ 1 ）$ 点 $M$ 和点 $N$ ；点 $B$ 和点 $D$ 是关于点 $O$ 的对称点； $（ 2 ）$ 直线 $B D$ 必经过点 $O$ ； $（ 3 ）$ 四边形 $A B C D$ 是中心对称图形； $（ 4 ）$ 四边形 $D M O C$ 和四边形 $B N O A$ 的面积相等； $（ 5 ） △ A O M$ 和 $△ C O N$ 成中心对称．
其中，正确的有（）

A、 $2$ 个 B、 $3$ 个 C、 $5$ 个 D、 $1$ 个

查看试题解析

二、填空题：本题共3小题，每小题3分，共9分。

17. $（ \sqrt{3} - \sqrt{2} ）^{0} + \sqrt{27} =$ ．

查看试题解析
18. 如图，每个小正方形的边长为 $1$ ，则 $∠ A B C$ 的度数为．

查看试题解析
19. 如图， $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 10 c m$ ， $B C = 6 c m$ ，动点 $P$ 从点 $C$ 出发，以每秒 $2 c m$ 的速度按 $C \to A$ 的路径运动，设运动时间为 $t$ 秒 $.$ 出发 $2$ 秒时， $A P =$ $c m$ ， $△ A B P$ 的面积为 $c m^{2}$ ， $t =$ 时， $B P$ 恰好平分 $∠ A B C$ ．

查看试题解析

三、解答题：本题共6小题，共48分。解答应写出文字说明，证明过程或演算步骤。

20. 先化简，再求值： $\frac{x^{2} + 3 x}{x + 3} + \frac{4 x^{2} - 1}{2 x - 1}$ ，其中 $x = \frac{1}{\sqrt{2} + 1}$ ．

查看试题解析
21. 已知 $a$ ， $b$ ， $m$ 都是实数，若 $a + b = 2$ ，则称 $a$ 与 $b$ 是关于 $l$ 的“平衡数”．

(1)、 $4$ 与是关于 $l$ 的“平衡数”， $3 - \sqrt{2}$ 与是关于 $l$ 的“平衡数”；

(2)、若 $（ m + \sqrt{3} ）（ 1 - \sqrt{3} ） = - 2$ ，判断 $m + \sqrt{3}$ 与 $2 - \sqrt{3}$ 是否是关于 $l$ 的“平衡数”，并说明理由．

查看试题解析
22. 如图，在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的中线， $D E ⊥ A B$ 于点 $E$ ， $D F ⊥ A C$ 于点 $F$ ，且 $D E = D F$ ．
求证：

(1)、 $△ B D E$ ≌ $△ C D F$ ；

(2)、 $A D ⊥ B C$ ．

查看试题解析
23.

(1)、如图 $1$ ， $△ A B C$ 中， $A B \neq A C$ ， $∠ A B C$ ， $∠ A C B$ 的平分线交于 $O$ 点，过 $O$ 点作 $E F / / B C$ 交 $A B$ ， $A C$ 于点 $E$ ， $F .$ 图中有个等腰三角形 $.$ 猜想： $E F$ 与 $B E$ ， $C F$ 之间有怎样的关系，并说明理由；

(2)、如图 $2$ ，若 $A B = A C$ ，其他条件不变，图中有个等腰三角形； $E F$ 与 $B E$ ， $C F$ 间的关系是；

(3)、如图 $3$ ， $A B \neq A C$ ，若 $∠ A B C$ 的角平分线与 $△ A B C$ 外角 $∠ A C D$ 的角平分线交于点 $O$ ，过点 $O$ 作 $O E / / B C$ 交 $A B$ 于 $E$ ，交 $A C$ 于 $F .$ 图中有个等腰三角形 $. E F$ 与 $B E$ ， $C F$ 间的数量关系是．

查看试题解析
24. 永州市万达广场筹建之初的一项挖土工程招标时，接到甲、乙两个工程队的投标书，每施工一天，需付甲工程队工程款2.4万元，付乙工程队工程款1.8万元，工程领导小组根据甲、乙两队的投标书测算，可有三种施工方案：
(方案一)甲队单独完成这项工程，刚好按规定工期完成；
(方案二)乙队单独完成这项工程要比规定工期多用6天；
(方案三)若由甲、乙两队合作做5天，剩下的工程由乙队单独做，也正好按规定工期完工．

(1)、请你求出完成这项工程的规定时间；

(2)、如果你是工程领导小组的组长，为了节省工程款，同时又能如期完工，你将选择哪一种方案?说明理由．

查看试题解析
25. 已知 $△ A B C$ 中， $∠ A = 90 °$ ， $A B = A C$ ，点 $D$ 为 $B C$ 的中点．

(1)、如图 $1$ ，点 $E$ 、 $F$ 分别为线段 $A B$ 、 $A C$ 上的点，当 $B E = A F$ 时，易得 $△ D E F$ 为三角形；

(2)、如图 $2$ ，若点 $E$ 、 $F$ 分别为 $A B$ 、 $C A$ 延长线上的点，且 $B E = A F$ ，其他条件不变，则 $（ 1 ）$ 中的结论仍然成立，请证明这个结论；

(3)、如图 $3$ ，若把一块三角尺的直角顶点放在点 $D$ 处转动，三角尺的两条直角边与线段 $A B$ 、 $A C$ 分别交于点 $E$ 、 $F$ ，请判断 $△ D E F$ 的形状，并证明你的结论．

查看试题解析