河北省沧州市献县2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-04-01 类型:期末考试
一、选择题(本大题共16个小题,1~10小题,每小题3分;11~16小题,每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 抛物线 与 轴的交点坐标是( )A、 B、 C、 D、3. 如图,ABCD为圆内接四边形,若∠A=60°,则∠C等于( )
2. 抛物线 与 轴的交点坐标是( )A、 B、 C、 D、3. 如图,ABCD为圆内接四边形,若∠A=60°,则∠C等于( ) A、30° B、60° C、120° D、300°4. 在如图所示的电路中,随机闭合开关S1 , S2 , S3中的两个,能让灯泡L1发光的概率是( )
A、30° B、60° C、120° D、300°4. 在如图所示的电路中,随机闭合开关S1 , S2 , S3中的两个,能让灯泡L1发光的概率是( )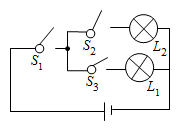 A、 B、 C、 D、5. 已知线段 , , 是线段 , 的比例中项,则线段的长为( )A、或 B、 C、 D、6. 反比例函数的图象在第一、第三象限,则m可能取的一个值为( )A、﹣1 B、0 C、1 D、27. 学校艺术节上,同学们绘制了非常美丽的画并且在其周围裱上等宽的边框做成艺术墙.下面是王亮从艺术墙上选取的四幅形状不同的作品,在同一幅作品中,内、外边框的图形不一定相似的是( )A、
A、 B、 C、 D、5. 已知线段 , , 是线段 , 的比例中项,则线段的长为( )A、或 B、 C、 D、6. 反比例函数的图象在第一、第三象限,则m可能取的一个值为( )A、﹣1 B、0 C、1 D、27. 学校艺术节上,同学们绘制了非常美丽的画并且在其周围裱上等宽的边框做成艺术墙.下面是王亮从艺术墙上选取的四幅形状不同的作品,在同一幅作品中,内、外边框的图形不一定相似的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为5m的墙,隔离区分成两个区域,中间用塑料膜隔开。已知整个隔离区塑料膜总长为12m,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长。小明认为:隔离区的最大面积为12m2;小亮认为:隔离区的面积可能为9m2。则:( )
8. 如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为5m的墙,隔离区分成两个区域,中间用塑料膜隔开。已知整个隔离区塑料膜总长为12m,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长。小明认为:隔离区的最大面积为12m2;小亮认为:隔离区的面积可能为9m2。则:( )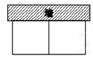 A、小明正确,小亮错误 B、小明错误,小亮正确 C、两人均正确 D、两人均错误9. 下列事件中是不可能事件的是( )A、守株待兔 B、瓮中捉鳖 C、水中捞月 D、百步穿杨10. 小明同学是一位古诗文的爱好者,在学习了一元二次方程这一章后,改编 了苏轼诗词《念奴娇·赤壁怀古》:“大江东去浪淘尽,千古风流人物.而立之年督东吴,早逝英年两位数.十位恰小个位三,个位平方与寿同.哪位学子算得快,多少年华数周瑜?”假设周瑜去世时年龄的十位数字是 ,则可列方程为( )A、 B、 C、 D、11. 已知点(-2,a),(2,b),(3,c)在函数的图象上,则下列关于a,b,c的大小关系判断中,正确的是( )A、a<b<c B、b<a<c C、c<b<a D、a<c<b12. 已知圆锥的母线长为10,侧面展开图面积为60π,则该圆锥的底面圆的半径长等于( )A、4 B、6 C、8 D、1213. 公元前3世纪,古希腊科学家阿基米德发现:若两物体与支点的距离与其重量成反比,则杠杆平衡.后来人们把它归纳为“杠杆原理”.通俗地说,已知阻力和阻力臂分别为1200N和0.5m,那么动力( )和动力臂为1.5m.
A、小明正确,小亮错误 B、小明错误,小亮正确 C、两人均正确 D、两人均错误9. 下列事件中是不可能事件的是( )A、守株待兔 B、瓮中捉鳖 C、水中捞月 D、百步穿杨10. 小明同学是一位古诗文的爱好者,在学习了一元二次方程这一章后,改编 了苏轼诗词《念奴娇·赤壁怀古》:“大江东去浪淘尽,千古风流人物.而立之年督东吴,早逝英年两位数.十位恰小个位三,个位平方与寿同.哪位学子算得快,多少年华数周瑜?”假设周瑜去世时年龄的十位数字是 ,则可列方程为( )A、 B、 C、 D、11. 已知点(-2,a),(2,b),(3,c)在函数的图象上,则下列关于a,b,c的大小关系判断中,正确的是( )A、a<b<c B、b<a<c C、c<b<a D、a<c<b12. 已知圆锥的母线长为10,侧面展开图面积为60π,则该圆锥的底面圆的半径长等于( )A、4 B、6 C、8 D、1213. 公元前3世纪,古希腊科学家阿基米德发现:若两物体与支点的距离与其重量成反比,则杠杆平衡.后来人们把它归纳为“杠杆原理”.通俗地说,已知阻力和阻力臂分别为1200N和0.5m,那么动力( )和动力臂为1.5m. A、360N B、400N C、450N D、500N14. 已知P,Q是线段AB的两个黄金分割点,且AB=10,则PQ长为( )A、5( -1) B、5( +1) C、10( -2) D、5(3- )15. 一列实数a1 , a2 , a3 , …,an,其中a1=﹣1,a2=== , a3= , …,an= , 则a1a2a3…a2021的结果为( )A、﹣ B、 C、673 D、﹣202116. 如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O , 点P是BD上的一个动点,过点P作EF∥AC , 分别交正方形的两条边于点E , F , 连接OE , OF , 设BP=x , △OEF的面积为y , 则能大致反映y与x之间的函数关系的图像为( )
A、360N B、400N C、450N D、500N14. 已知P,Q是线段AB的两个黄金分割点,且AB=10,则PQ长为( )A、5( -1) B、5( +1) C、10( -2) D、5(3- )15. 一列实数a1 , a2 , a3 , …,an,其中a1=﹣1,a2=== , a3= , …,an= , 则a1a2a3…a2021的结果为( )A、﹣ B、 C、673 D、﹣202116. 如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O , 点P是BD上的一个动点,过点P作EF∥AC , 分别交正方形的两条边于点E , F , 连接OE , OF , 设BP=x , △OEF的面积为y , 则能大致反映y与x之间的函数关系的图像为( )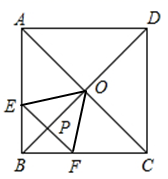 A、
A、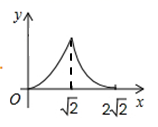 B、
B、 C、
C、 D、
D、
二、填空题(本大题每空3分,共计12分)
-
17. 如图,某十字路口设有交通信号灯,东西向信号灯的开启规律如下:红灯开启30秒后,紧接着绿灯开启42秒,再紧接着黄灯开启3秒,按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是.
 18. 学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=6m,AB=1.2m,CO=1m,则栏杆C端应下降的垂直距离CD为m.
18. 学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=6m,AB=1.2m,CO=1m,则栏杆C端应下降的垂直距离CD为m. 19. 用绘图软件绘制双曲线 : 与动直线 : ,且交于一点,图1为 时的视窗情形.
19. 用绘图软件绘制双曲线 : 与动直线 : ,且交于一点,图1为 时的视窗情形.
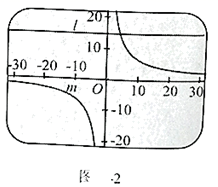 (1)、当 时, 与 的交点坐标为;(2)、视窗的大小不变,但其可视范围可以变化,且变化前后原点 始终在视窗中心.例如,为在视窗中看到(1)中的交点,可将图1中坐标系的单位长度变为原来的 ,其可视范围就由 及 变成了 及 (如图2).当 和 时, 与 的交点分别是点A和 ,为能看到 在A和 之间的一整段图象,需要将图1中坐标系的单位长度至少变为原来的 ,则整数 .
(1)、当 时, 与 的交点坐标为;(2)、视窗的大小不变,但其可视范围可以变化,且变化前后原点 始终在视窗中心.例如,为在视窗中看到(1)中的交点,可将图1中坐标系的单位长度变为原来的 ,其可视范围就由 及 变成了 及 (如图2).当 和 时, 与 的交点分别是点A和 ,为能看到 在A和 之间的一整段图象,需要将图1中坐标系的单位长度至少变为原来的 ,则整数 .三、解答题(本大题共7个小题,共66分)
-
20. 在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感.按此比例,如果雕像的高为 , 那么它的下部应设计多高?21. 已知两个有理数和5,(1)、计算:;(2)、若再添一个负整数m,且 , 5与m的平均数仍小于m,求m的值.22. 某博物馆展厅的俯视示意图如图1所示,嘉淇进入展厅后开始自由参观,每走到一个十字道口,她自己可能直行,也可能向左转或向右转,且这三种可能性均相同.
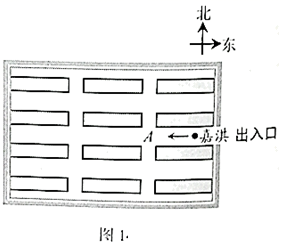
 (1)、求嘉淇走到十字道口 向北走的概率;(2)、补全图2的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大.23. 如图,AB是⊙O的弦,半径OD⊥AB,垂足为C,点E在⊙O上,连接OA、DE、BE.
(1)、求嘉淇走到十字道口 向北走的概率;(2)、补全图2的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大.23. 如图,AB是⊙O的弦,半径OD⊥AB,垂足为C,点E在⊙O上,连接OA、DE、BE. (1)、若∠DEB=30°,求∠AOD的度数;(2)、若CD=2,弦AB=8,求⊙O的半径长.24. 如图,直线y=x+m与双曲线y=相交于A(2,1)、B两点.
(1)、若∠DEB=30°,求∠AOD的度数;(2)、若CD=2,弦AB=8,求⊙O的半径长.24. 如图,直线y=x+m与双曲线y=相交于A(2,1)、B两点. (1)、求m及k的值.(2)、求出S△AOB的面积.(3)、直接写出x+m﹣>0时x的取值范围.25. 某商场准备在济宁义乌批发城采购一批特色商品,经调查,用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.(1)、求一件A、B型商品的进价分别为多少元?(2)、若该商场购进A、B型商品共160件进行试销,其中A型商品的件数不小于B型的件数,且总成本不能超过24840元,则共有几种进货方案?(3)、已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出,在第(2)问条件下,哪种方案利润最大?并求出最大利润.26. 如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.
(1)、求m及k的值.(2)、求出S△AOB的面积.(3)、直接写出x+m﹣>0时x的取值范围.25. 某商场准备在济宁义乌批发城采购一批特色商品,经调查,用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.(1)、求一件A、B型商品的进价分别为多少元?(2)、若该商场购进A、B型商品共160件进行试销,其中A型商品的件数不小于B型的件数,且总成本不能超过24840元,则共有几种进货方案?(3)、已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出,在第(2)问条件下,哪种方案利润最大?并求出最大利润.26. 如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.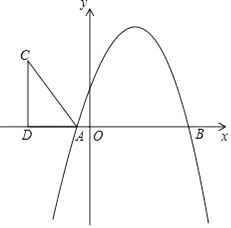 (1)、求抛物线的解析式;(2)、在第二象限内取一点C,作CD垂直x轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(1)、求抛物线的解析式;(2)、在第二象限内取一点C,作CD垂直x轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)、在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.