河北省邯郸市馆陶县2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-04-01 类型:期末考试
一、选择题(本大题共16个小题,共38分,1~6小题每小题3分,7~16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 如图,在中, , 若 , 则是( )
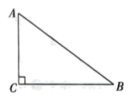 A、 B、 C、 D、2. 以机场为观测点,飞机甲在北偏东方向处.则南偏东方向的是( )
A、 B、 C、 D、2. 以机场为观测点,飞机甲在北偏东方向处.则南偏东方向的是( ) A、乙 B、丙 C、丁 D、戊3. 某两地的实际距离为千米,画在地图上的距离是厘米,则在地图上的距离与实际的距离之比是( ).A、 B、 C、 D、4. 若反比例函数的图象位于第二、四象限,则的取值可以是( )A、0 B、1 C、2 D、35. 甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差如图所示,根据图中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A、乙 B、丙 C、丁 D、戊3. 某两地的实际距离为千米,画在地图上的距离是厘米,则在地图上的距离与实际的距离之比是( ).A、 B、 C、 D、4. 若反比例函数的图象位于第二、四象限,则的取值可以是( )A、0 B、1 C、2 D、35. 甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差如图所示,根据图中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( ) A、甲 B、乙 C、丙 D、丁6. 如图,小康利用复印机将一张长为 , 宽为的矩形图片放大,其中放大后的长为 , 则放大后的矩形的面积为( )
A、甲 B、乙 C、丙 D、丁6. 如图,小康利用复印机将一张长为 , 宽为的矩形图片放大,其中放大后的长为 , 则放大后的矩形的面积为( )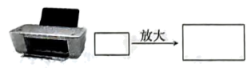 A、 B、 C、 D、7. 把抛物线y=x2向左平移2个单位得到的抛物线是( )A、y=(x+2)2 B、y=(x﹣2)2 C、y=x2+2 D、y=x2﹣28. 行道树是指种在道路两旁及分车带,给车辆和行人遮荫并构成街景的树种.国槐是我市常见的行道树品种.下图是一批国槐树苗移植成活频率的统计图,由此可估计这种树苗移植成活的概率约为( )
A、 B、 C、 D、7. 把抛物线y=x2向左平移2个单位得到的抛物线是( )A、y=(x+2)2 B、y=(x﹣2)2 C、y=x2+2 D、y=x2﹣28. 行道树是指种在道路两旁及分车带,给车辆和行人遮荫并构成街景的树种.国槐是我市常见的行道树品种.下图是一批国槐树苗移植成活频率的统计图,由此可估计这种树苗移植成活的概率约为( ) A、0.95 B、0.90 C、0.85 D、0.809. 某快递员十二月份送餐统计数据如下表:
A、0.95 B、0.90 C、0.85 D、0.809. 某快递员十二月份送餐统计数据如下表:送餐距离
小于等于3公里
大于3公里
占比
送餐费
4元单
6元单
则该快递员十二月份平均每单送餐费是( )
A、元 B、元 C、5元 D、元10. 在四个密闭容器中分别装有甲、乙、丙、丁四种气体,如图,用四个点分别描述这四种气体的密度与体积的情况,其中描述乙、丁两种气体情况的点恰好在同一个反比例函数的阁象上,则这四种气体的质量最小的是( ) A、甲 B、乙 C、丙 D、丁11. 为了解“睡眠管理”落实情况,某初中学校随机调查50名学生每天平均睡眠时间(时间均保留整数),将样本数据绘制成统计图(如图),其中有两个数据被遮盖关于睡眠时间的统计量中,与被遮盖的数据无关的是( )
A、甲 B、乙 C、丙 D、丁11. 为了解“睡眠管理”落实情况,某初中学校随机调查50名学生每天平均睡眠时间(时间均保留整数),将样本数据绘制成统计图(如图),其中有两个数据被遮盖关于睡眠时间的统计量中,与被遮盖的数据无关的是( )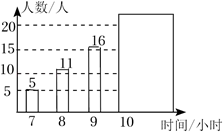 A、平均数 B、中位数 C、众数 D、方差12. 如图,的半径弦于点E , C是上一点, , 的最大值为18,则的长为( )
A、平均数 B、中位数 C、众数 D、方差12. 如图,的半径弦于点E , C是上一点, , 的最大值为18,则的长为( ) A、8 B、6 C、4 D、213. 如图,与都是等边三角形,固定 , 将从图示位置绕点C逆时针旋转一周,在旋转的过程中,与位似的位置有( )
A、8 B、6 C、4 D、213. 如图,与都是等边三角形,固定 , 将从图示位置绕点C逆时针旋转一周,在旋转的过程中,与位似的位置有( ) A、个 B、个 C、个 D、个及个以上14. 如图,正十边形与正方形共边 , 延长正方形的一边与正十边形的一边 , 两线交于点F , 设 , 则x的值为( ).
A、个 B、个 C、个 D、个及个以上14. 如图,正十边形与正方形共边 , 延长正方形的一边与正十边形的一边 , 两线交于点F , 设 , 则x的值为( ). A、15 B、18 C、21 D、2415. 题目:“如图,在中, , , , 以点为圆心的的半径为 , 若对于的一个值,与只有一个交点,求的取值范围.”对于其答案,甲答: . 乙答: . 丙答: . 则正确的是( )
A、15 B、18 C、21 D、2415. 题目:“如图,在中, , , , 以点为圆心的的半径为 , 若对于的一个值,与只有一个交点,求的取值范围.”对于其答案,甲答: . 乙答: . 丙答: . 则正确的是( ) A、只有乙答的对 B、甲、乙的答案合在一起才完整 C、乙、丙的答案合在一起才完整 D、三人的答案合在一起才完整16. 如图,二次函数的图象与x轴的交点为A、D的横坐标分别为3和 , 其图像与x轴围成封闭图形L , 图形L内部(不包含边界)恰有4个整点(横纵坐标均为整数的点),系数a的值可以是( )
A、只有乙答的对 B、甲、乙的答案合在一起才完整 C、乙、丙的答案合在一起才完整 D、三人的答案合在一起才完整16. 如图,二次函数的图象与x轴的交点为A、D的横坐标分别为3和 , 其图像与x轴围成封闭图形L , 图形L内部(不包含边界)恰有4个整点(横纵坐标均为整数的点),系数a的值可以是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共3个小题,共10分,17小题2分,18~19小题各4分,每空2分)
-
17. 将一元二次方程化成一般形式之后,若二次项的系数是2,则一次项系数为.18. 如图,将刻度尺、含角的直角三角板和量角器如图摆放(无重叠部分),若三角板角的顶点A在刻度尺上的读数是 , 量角器与刻度尺接触点在刻度尺上的读数是 , 量角器与三角板的接触点为B .
 (1)、 .(2)、该量角器的直径长为 . (结果保留根号)19. 如图,在中, , , ,
(1)、 .(2)、该量角器的直径长为 . (结果保留根号)19. 如图,在中, , , , (1)、 .(2)、现有动点从点出发,沿向点方向运动,动点从点出发,沿线段向点方向运动,如果点的速度是 , 点的速度是 . 、两点同时出发,当有一点到达所在线段的端点时,另一点停止运动.设运动时间为秒.当时,平分的面积.
(1)、 .(2)、现有动点从点出发,沿向点方向运动,动点从点出发,沿线段向点方向运动,如果点的速度是 , 点的速度是 . 、两点同时出发,当有一点到达所在线段的端点时,另一点停止运动.设运动时间为秒.当时,平分的面积.三、解答题(本大题共7个小题,共72分,解答应写出文字说明、证明过程或演算步骤)
-
20. 已知反比例函数图象经过 .(1)、求的值;(2)、若点 , 是反比例函数图象上两点,试比较 , 大小.21. 老师在黑板上书写了一个正确的演算过程,随后用手掌遮住了一部分,如图所示.
 (1)、若所捂的部分为0,求x的值;(2)、若所捂的部分是常数a , 若该方程有实数根,求a的取值范围.22. 如图,在平行四边形中,点在边上,点在的延长线上,且 .
(1)、若所捂的部分为0,求x的值;(2)、若所捂的部分是常数a , 若该方程有实数根,求a的取值范围.22. 如图,在平行四边形中,点在边上,点在的延长线上,且 . (1)、求证:;(2)、若 , 求的长.23. 某教室的开关控制板上有四个外形完全相同的开关,其中两个分别控制A、B两盏电灯,另两个分别控制C、D两个吊扇.已知电灯、吊扇均正常,且处于不工作状态,开关与电灯、电扇的对应关系未知.
(1)、求证:;(2)、若 , 求的长.23. 某教室的开关控制板上有四个外形完全相同的开关,其中两个分别控制A、B两盏电灯,另两个分别控制C、D两个吊扇.已知电灯、吊扇均正常,且处于不工作状态,开关与电灯、电扇的对应关系未知.
(1)、若四个开关均正常,则任意按下一个开关,正好一盏灯亮的概率是多少?
(2)、若其中一个控制电灯的开关坏了,则任意按下两个开关,正好一盏灯亮和一个扇转的概率是多少?请用树状图法或列表法加以说明.
24. 如图,某隧道的横截面可以看作由半圆O与矩形组成,所在直线表示地平面,E点表示隧道内的壁灯,已知 , 从A点观测E点的仰角为 , 观测C点的俯角为(参考数据的值取4). (1)、求长;(2)、求壁灯的高度.25. 随着自动化设备的普及,公园中引入了自动喷灌系统.图1是某公园内的一个可垂直升降的草坪喷灌器,从喷水口喷出的水柱均为形状相同的抛物线,图2是该喷灌器喷水时的截面示意图.
(1)、求长;(2)、求壁灯的高度.25. 随着自动化设备的普及,公园中引入了自动喷灌系统.图1是某公园内的一个可垂直升降的草坪喷灌器,从喷水口喷出的水柱均为形状相同的抛物线,图2是该喷灌器喷水时的截面示意图. (1)、喷水口A离地高度为 , 喷出的水柱在离喷水口水平距离为处达到最高,高度为 , 且水柱刚好落在公园围栏和地面的交界B处.
(1)、喷水口A离地高度为 , 喷出的水柱在离喷水口水平距离为处达到最高,高度为 , 且水柱刚好落在公园围栏和地面的交界B处.①在图2中建立合适的平面直角坐标系,并求出抛物线的解析式;
②求喷灌器底端O到点B的距离;
(2)、现准备在公园内沿围栏建花坛,花坛的截面示意图为矩形(如图3),其中高为.宽为.为达到给花坛喷灌的效果,需将喷水口A向上升高 , 使水柱落在花坛的上方边上,求h的取值范围.26. 如图,在矩形中, , , , 垂足为E . F是点E关于的对称点,连接 . (1)、求证:;(2)、求和的长;(3)、将一个与完全重合的透明三角板沿射线方向平移.
(1)、求证:;(2)、求和的长;(3)、将一个与完全重合的透明三角板沿射线方向平移.①设点在上移动的距离是m . 当点分别落在线段上时,求相应的m的值;
②当点落在上时,立刻将绕点顺时针旋转,且旋转60°时停止.点H在上,且 . 若平移的速度为每秒1个单位长度,绕点旋转的速度为每秒5°,在整个运动过程中,直接写出点H在区域(含边界)内的时长.