河北省石家庄市高邑县2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-04-01 类型:期末考试
一、选择题
-
1. 掷一枚质地均匀的标有1,2,3,4,5,6六个数字的立方体骰子,骰子停止后,出现可能性最小的是( )A、大于3的点数 B、小于3的点数 C、大于5的点数 D、小于5的点数2. 一组数据1,x,5,7有唯一众数,且中位数是6,则平均数是( )A、6 B、5 C、4 D、33. 如图是由4个相同的小正方体组成的立体图形,则下面四个平面图形中不是这个立体图形的三视图的是( )
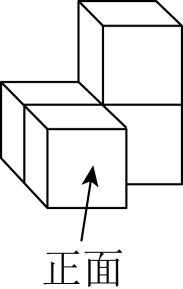 A、
A、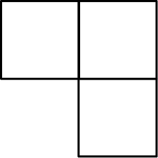 B、
B、 C、
C、 D、
D、 4. 若关于的一元二次方程有两个不相等的实数根,则反比例函数的图象在( )A、第一、三象限 B、第二、四象限 C、第二、三象限 D、第一、四象限5. 若点 , , 在反比例函数的图象上,则下列结论中正确的是( )A、 B、 C、 D、6. 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
4. 若关于的一元二次方程有两个不相等的实数根,则反比例函数的图象在( )A、第一、三象限 B、第二、四象限 C、第二、三象限 D、第一、四象限5. 若点 , , 在反比例函数的图象上,则下列结论中正确的是( )A、 B、 C、 D、6. 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( ) A、50° B、80° C、100° D、130°7. 如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为( )
A、50° B、80° C、100° D、130°7. 如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为( ) A、2 B、4 C、4 D、88. 如图,中, , , . 将沿图中的虚线剪开,下列四种剪开的方法中,剪下的阴影三角形一定与原三角形相似的是( )
A、2 B、4 C、4 D、88. 如图,中, , , . 将沿图中的虚线剪开,下列四种剪开的方法中,剪下的阴影三角形一定与原三角形相似的是( ) A、①②③ B、③④ C、①②③④ D、①②④9. 如图,在平面直角坐标系xOy中,以原点O为位似中心,把线段AB放大后得到线段CD.若点A(1,2),B(2,0),D(5,0),则点A的对应点C的坐标是( )
A、①②③ B、③④ C、①②③④ D、①②④9. 如图,在平面直角坐标系xOy中,以原点O为位似中心,把线段AB放大后得到线段CD.若点A(1,2),B(2,0),D(5,0),则点A的对应点C的坐标是( )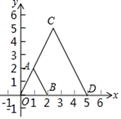 A、(2,5) B、( ,5) C、(3,5) D、(3,6)10. 如图,中, ,点D在上, . 若 , 则的长度为( )
A、(2,5) B、( ,5) C、(3,5) D、(3,6)10. 如图,中, ,点D在上, . 若 , 则的长度为( ) A、 B、 C、 D、11. 如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为 米,则斜坡AB的长度为( )
A、 B、 C、 D、11. 如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为 米,则斜坡AB的长度为( ) A、 B、 C、 D、2412. 如图,用一个圆心角为的扇形纸片围成一个底面半径为2,侧面积为的圆锥体,则该扇形的圆心角得大小为( )
A、 B、 C、 D、2412. 如图,用一个圆心角为的扇形纸片围成一个底面半径为2,侧面积为的圆锥体,则该扇形的圆心角得大小为( ) A、90° B、120° C、150° D、180°13. 如图,把圆分成六等分,经过各分点作圆的切线,以相邻切线的交点为顶点的图形是这个圆的外切正六边形, 的半径是R,它的外切正六边形的边长为( )
A、90° B、120° C、150° D、180°13. 如图,把圆分成六等分,经过各分点作圆的切线,以相邻切线的交点为顶点的图形是这个圆的外切正六边形, 的半径是R,它的外切正六边形的边长为( ) A、 B、 C、 D、14. 在一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机地摸出一个小球然后放回,再随机地摸出一个小球,则两次摸出的小球的标号之和等于6的概率是( )A、 B、 C、 D、15. 有一个人患了流行性感冒,经过两轮传染后共有144人患了流行性感冒,则每轮传染中平均一个人传染的人数是( )A、14 B、11 C、10 D、916. 对于题目“抛物线l1:(﹣1<x≤2)与直线l2:y=m(m为整数)只有一个交点,确定m的值”;甲的结果是m=1或m=2;乙的结果是m=4,则( )A、只有甲的结果正确 B、只有乙的结果正确 C、甲、乙的结果合起来才正确 D、甲、乙的结果合起来也不正确
A、 B、 C、 D、14. 在一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机地摸出一个小球然后放回,再随机地摸出一个小球,则两次摸出的小球的标号之和等于6的概率是( )A、 B、 C、 D、15. 有一个人患了流行性感冒,经过两轮传染后共有144人患了流行性感冒,则每轮传染中平均一个人传染的人数是( )A、14 B、11 C、10 D、916. 对于题目“抛物线l1:(﹣1<x≤2)与直线l2:y=m(m为整数)只有一个交点,确定m的值”;甲的结果是m=1或m=2;乙的结果是m=4,则( )A、只有甲的结果正确 B、只有乙的结果正确 C、甲、乙的结果合起来才正确 D、甲、乙的结果合起来也不正确二、填空题
-
17. 已知点P是线段上的黄金分割点,且 , , 则 .18. 一座抛物线形拱桥如图所示,桥下水面宽度为4m时,拱顶距离水面是2m,当水位下降1m后,水面的宽度为m.(结果保留根号)
 19. 曲线L在直角坐标系中的位置如图所示,曲线L是由半径为2,圆心角为120°的(O是坐标原点,点A在x轴上)绕点A旋转180°,得到;再将绕点旋转180°,得到;……依次类推,形成曲线L , 现有一点P从O点出发,以每秒个单位长度的速度,沿曲线L向右运动,则点A的坐标为;在第2020s时,点P的坐标为 .
19. 曲线L在直角坐标系中的位置如图所示,曲线L是由半径为2,圆心角为120°的(O是坐标原点,点A在x轴上)绕点A旋转180°,得到;再将绕点旋转180°,得到;……依次类推,形成曲线L , 现有一点P从O点出发,以每秒个单位长度的速度,沿曲线L向右运动,则点A的坐标为;在第2020s时,点P的坐标为 .
三、解答题
-
20. 已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根.
(1)、求k的取值范围;
(2)、若此方程的两实数根x1 , x2满足x12+x22=11,求k的值.21. 消防车是救援火灾的主要装备,图①是一辆登高云梯消防车的实物图,图②是其工作示意图,起重臂(20米30米)是可伸缩的,且起重臂可绕点A在一定范围内上下转动张角 , 转动点A距离地面的高度为4米.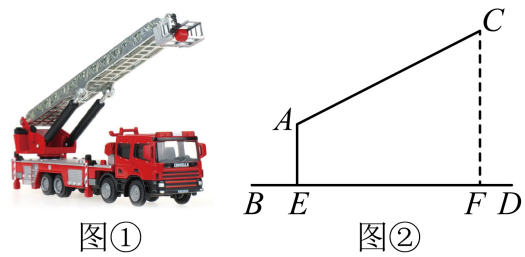 (1)、当起重臂的长度为24米,张角时,云梯消防车最高点C距离地面的高度的长为米.(2)、某日一栋大楼突发火灾,着火点距离地面的高度为26米,该消防车在这栋楼下能否实施有效救援?请说明理由(参考数据:)(提示:当起重臂伸到最长且张角最大时,云梯顶端C可以达到最大高度)22. 有甲、乙、丙三张完全相同的卡片,小明在其正面各写上一个方程,如图,然后将这三张卡片背面朝上洗匀.
(1)、当起重臂的长度为24米,张角时,云梯消防车最高点C距离地面的高度的长为米.(2)、某日一栋大楼突发火灾,着火点距离地面的高度为26米,该消防车在这栋楼下能否实施有效救援?请说明理由(参考数据:)(提示:当起重臂伸到最长且张角最大时,云梯顶端C可以达到最大高度)22. 有甲、乙、丙三张完全相同的卡片,小明在其正面各写上一个方程,如图,然后将这三张卡片背面朝上洗匀. (1)、从中随机抽取一张,求抽到方程没有实数根的概率;(2)、从中随机抽取一张,记下方程后放回,再随机抽取一张,请用列表或面树状图的方法,求抽到的方程都有实数根的概率.23. 如图,点的坐标是 , 过点作轴的平行线交轴于点A , 交双曲线()于点 , 作交双曲线()于点 , 连接 . 已知 .
(1)、从中随机抽取一张,求抽到方程没有实数根的概率;(2)、从中随机抽取一张,记下方程后放回,再随机抽取一张,请用列表或面树状图的方法,求抽到的方程都有实数根的概率.23. 如图,点的坐标是 , 过点作轴的平行线交轴于点A , 交双曲线()于点 , 作交双曲线()于点 , 连接 . 已知 . (1)、求的值;(2)、求的面积.24. 如图,为的直径,为的半径,的弦与相交于点F,的切线交的延长线于点E,.
(1)、求的值;(2)、求的面积.24. 如图,为的直径,为的半径,的弦与相交于点F,的切线交的延长线于点E,. (1)、求证:垂直平分;(2)、若的半径长为3,且 , 求的长.25. 某水果超市以每千克20元的价格购进一批樱桃,规定每千克樱桃售价不低于进价又不高于40元,经市场调查发现,樱桃的日销售量y(千克)与每千克售价x(元)满足一次函数关系 ,(1)、该超市要想获得1000元的日销售利润,每千克樱桃的售价应定为多少元?(2)、当每千克樱桃的售价定为多少元时,日销售利润最大?最大利润是多少?26. 如图,抛物线经过 , 两点,并且与轴交于点 .
(1)、求证:垂直平分;(2)、若的半径长为3,且 , 求的长.25. 某水果超市以每千克20元的价格购进一批樱桃,规定每千克樱桃售价不低于进价又不高于40元,经市场调查发现,樱桃的日销售量y(千克)与每千克售价x(元)满足一次函数关系 ,(1)、该超市要想获得1000元的日销售利润,每千克樱桃的售价应定为多少元?(2)、当每千克樱桃的售价定为多少元时,日销售利润最大?最大利润是多少?26. 如图,抛物线经过 , 两点,并且与轴交于点 . (1)、求此抛物线的解析式;(2)、直接写出直线的解析式为;(3)、若点是第一象限的抛物线上的点,且横坐标为 , 过点作轴的垂线交于点 , 设的长为 , 求与之间的函数关系式及的最大值;(4)、在轴的负半轴上是否存在点 , 使以 , , 三点为顶点的三角形为等腰三角形?如果存在,直接写出点的坐标;如果不存在,说明理由.
(1)、求此抛物线的解析式;(2)、直接写出直线的解析式为;(3)、若点是第一象限的抛物线上的点,且横坐标为 , 过点作轴的垂线交于点 , 设的长为 , 求与之间的函数关系式及的最大值;(4)、在轴的负半轴上是否存在点 , 使以 , , 三点为顶点的三角形为等腰三角形?如果存在,直接写出点的坐标;如果不存在,说明理由.