河北省邯郸市永年区2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-04-01 类型:期末考试
一、单选题
-
1. 如图,若⊙的半径为6,圆心到一条直线的距离为6,则这条直线可能是( )
 A、 B、 C、 D、2. 某校举办了以“展礼仪风采,树文明形象”为主题的比赛.已知某位选手的礼仪服装、语言表达、举止形态这三项的得分分别为90分,80分,80分,若依次按照的百分比确定成绩,则该选手的成绩是( )A、86分 B、85分 C、84分 D、83分3. 如果函数是反比例函数,那么m的值是( )A、2 B、 C、1 D、4. 如图,点是上一点,若 , 则的度数为( )
A、 B、 C、 D、2. 某校举办了以“展礼仪风采,树文明形象”为主题的比赛.已知某位选手的礼仪服装、语言表达、举止形态这三项的得分分别为90分,80分,80分,若依次按照的百分比确定成绩,则该选手的成绩是( )A、86分 B、85分 C、84分 D、83分3. 如果函数是反比例函数,那么m的值是( )A、2 B、 C、1 D、4. 如图,点是上一点,若 , 则的度数为( ) A、 B、 C、 D、5. 如图,与位似,点O是它们的位似中心,且它们的周长比为 , 则与的面积之比是( )
A、 B、 C、 D、5. 如图,与位似,点O是它们的位似中心,且它们的周长比为 , 则与的面积之比是( ) A、 B、 C、 D、6. △ABC中,∠A,∠B均为锐角,且(tanB-)(2sinA-)=0,则△ABC是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、至少一个角是60°的三角形7. 在一次演讲比赛中,组委会邀请了7位评委为选手打分,并规定同时去掉一个最高分与最低分,将剩下5位评委的平均分作为该选手的最终得分.在7位评委的7个打分数据与后面保留的5个数据中,一定保持不变的统计量是( )A、平均数 B、中位数 C、众数 D、方差8. 如图所示的是二次函数的部分图象,由图象可知不等式的解集是( )
A、 B、 C、 D、6. △ABC中,∠A,∠B均为锐角,且(tanB-)(2sinA-)=0,则△ABC是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、至少一个角是60°的三角形7. 在一次演讲比赛中,组委会邀请了7位评委为选手打分,并规定同时去掉一个最高分与最低分,将剩下5位评委的平均分作为该选手的最终得分.在7位评委的7个打分数据与后面保留的5个数据中,一定保持不变的统计量是( )A、平均数 B、中位数 C、众数 D、方差8. 如图所示的是二次函数的部分图象,由图象可知不等式的解集是( ) A、 B、 C、且 D、或9. 如图,的内切圆圆O与 , , 分别相切于点D,E,F,若 , 则的度数是( )
A、 B、 C、且 D、或9. 如图,的内切圆圆O与 , , 分别相切于点D,E,F,若 , 则的度数是( ) A、 B、 C、 D、10. 若关于的一元二次方程有一个根为0,那么的值只能是( )A、1 B、1, C、 D、以上都不对11. 已知点 , 和都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、12. 如图,为的直径,弦交于点 , , , , 则( )
A、 B、 C、 D、10. 若关于的一元二次方程有一个根为0,那么的值只能是( )A、1 B、1, C、 D、以上都不对11. 已知点 , 和都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、12. 如图,为的直径,弦交于点 , , , , 则( )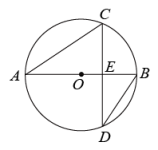 A、 B、 C、1 D、213. 如图,是斜靠在墙上的长梯,与地面夹角为 , 当梯顶下滑到时,梯脚滑到 , 与地面的夹角为 , 若 , , 则( )
A、 B、 C、1 D、213. 如图,是斜靠在墙上的长梯,与地面夹角为 , 当梯顶下滑到时,梯脚滑到 , 与地面的夹角为 , 若 , , 则( ) A、 B、 C、 D、14. 如图,矩形的顶点和正方形的顶点都在反比例函数的图像上,点的坐标为 , 则点的坐标为( )
A、 B、 C、 D、14. 如图,矩形的顶点和正方形的顶点都在反比例函数的图像上,点的坐标为 , 则点的坐标为( ) A、 B、 C、 D、15. 如图,小明周末晚上陪父母在马路上散步,他由灯下A处前进4米到达B处时,测得影子长为1米,已知小明身高1.6米,他若继续往前走4米到达D处,此时影子长为( )
A、 B、 C、 D、15. 如图,小明周末晚上陪父母在马路上散步,他由灯下A处前进4米到达B处时,测得影子长为1米,已知小明身高1.6米,他若继续往前走4米到达D处,此时影子长为( )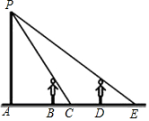 A、1米 B、2米 C、3米 D、4米16. 已知二次函数的图象如图所示,有下列4个结论:①;②;③;④;其中正确的结论有( )
A、1米 B、2米 C、3米 D、4米16. 已知二次函数的图象如图所示,有下列4个结论:①;②;③;④;其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
17. 若关于 的一元二次方程 配方后得到方程 , 则 的值为 .18. 如图,扇形AOB中,OA=10,∠AOB=36°.若将此扇形绕点B顺时针旋转,得一新扇形A′O′B,其中A点在O′B上,则点O的运动路径长为cm.(结果保留π)
 19. 如图,矩形ABCD中,AB=2cm,AD=5cm,动点P从点A出发,以1cm/s的速度沿AD向终点D移动,设移动时间为t(s).连接PC,以PC为一边作正方形PCEF,连接DE、DF,则△DEF面积最小值为 .
19. 如图,矩形ABCD中,AB=2cm,AD=5cm,动点P从点A出发,以1cm/s的速度沿AD向终点D移动,设移动时间为t(s).连接PC,以PC为一边作正方形PCEF,连接DE、DF,则△DEF面积最小值为 .
三、解答题
-
20. 学校组织七、八年级学生参加了“国家安全知识”测试(满分100分).已知七、八年级各有200人,现从两个年级分别随机抽取10名学生的测试成绩(单位:分)进行统计:
七年级 86,94,79,84,71,90,76,83,90,87
八年级 88,76,90,78,87,93,75,87,87,79
整理如下:
年级
平均数
中位数
众数
方差
七年级
84
90
八年级
84
87
根据以上信息,回答下列问题:
(1)、填空: , .同学说:“这次测试我得了86分,位于年级中等偏上水平”,由此可判断他是年级的学生;
(2)、学校规定测试成绩不低于85分为“优秀”,估计该校这两个年级测试成绩达到“优秀”的学生总人数;(3)、你认为哪个年级的学生掌握国家安全知识的总体水平较好?请给出一条理由.21. 已知关于x的一元二次方程(1)、求证:无论m为何值,方程总有实数根;(2)、若 , 是方程的两个实数根,且 , 求m的值.22. 小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为 ,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为 .已知山坡坡度 ,即 ,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据: ) 23. 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,连接DE,EF.已知四边形BFED是平行四边形,= .
23. 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,连接DE,EF.已知四边形BFED是平行四边形,= . (1)、若AB=8,求线段AD的长.(2)、若△ADE的面积为1,求平行四边形BFED的面积.24. 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y(m≠0)的图象相交于A,B两点,过点A作AD⊥x轴于点D,AO=5,OD:AD=3:4,B点的坐标为(﹣6,n)
(1)、若AB=8,求线段AD的长.(2)、若△ADE的面积为1,求平行四边形BFED的面积.24. 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y(m≠0)的图象相交于A,B两点,过点A作AD⊥x轴于点D,AO=5,OD:AD=3:4,B点的坐标为(﹣6,n) (1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、P是y轴上一点,且△AOP是等腰三角形,请直接写出所有符合条件的P点坐标.
(1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、P是y轴上一点,且△AOP是等腰三角形,请直接写出所有符合条件的P点坐标.
