河北省石家庄市桥西区2023-2024学年九年级上学期期末数学试卷
试卷更新日期:2024-04-01 类型:期末考试
一、选择题:本题共16小题,共42分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 如图,从左面观察这个立体图形,得到的平面图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列方程中是一元二次方程的是( )A、 B、 C、 D、3. 下列各点中,在反比例函数图象上的是( )A、 B、 C、 D、4. 一组数据:3,4,4,6,若添加一个数据6,则不发生变化的统计量是( )A、平均数 B、中位数 C、众数 D、方差5. 用配方法解一元二次方程时,配方后的方程是( )A、 B、 C、 D、6. 如图,点 , 分别在的两边 , 上, , 若 , , , 则为( )
2. 下列方程中是一元二次方程的是( )A、 B、 C、 D、3. 下列各点中,在反比例函数图象上的是( )A、 B、 C、 D、4. 一组数据:3,4,4,6,若添加一个数据6,则不发生变化的统计量是( )A、平均数 B、中位数 C、众数 D、方差5. 用配方法解一元二次方程时,配方后的方程是( )A、 B、 C、 D、6. 如图,点 , 分别在的两边 , 上, , 若 , , , 则为( ) A、 B、 C、 D、7. 已知:如图 , 是的两条半径,且 , 点在上,则的度数为( )
A、 B、 C、 D、7. 已知:如图 , 是的两条半径,且 , 点在上,则的度数为( ) A、 B、 C、 D、8. 正六边形最少旋转度后能与自身重合,则为( )A、 B、 C、 D、9. 若点 , 都在反比例函数的图象上,则 , 的大小关系是( )A、 B、 C、 D、不能确定10. 如图,与是以点为位似中心的位似图形,若:: , 则与的面积比是( )
A、 B、 C、 D、8. 正六边形最少旋转度后能与自身重合,则为( )A、 B、 C、 D、9. 若点 , 都在反比例函数的图象上,则 , 的大小关系是( )A、 B、 C、 D、不能确定10. 如图,与是以点为位似中心的位似图形,若:: , 则与的面积比是( ) A、: B、: C、: D、:11. 关于二次函数 , 下列说法不正确的是( )A、顶点坐标为 B、当时,随增大而减小 C、函数有最小值 D、当时,有最小值12. 某学校组织一次足球赛,采取单循环的比赛形式,即每两个球队之间都要比赛一场,计划组织支球队参加,安排场比赛,则为( )A、 B、 C、 D、13. 如图,在矩形中, , , 以点为圆心,长为半径画弧,交于点 , 连接 , 则扇形的面积为( )
A、: B、: C、: D、:11. 关于二次函数 , 下列说法不正确的是( )A、顶点坐标为 B、当时,随增大而减小 C、函数有最小值 D、当时,有最小值12. 某学校组织一次足球赛,采取单循环的比赛形式,即每两个球队之间都要比赛一场,计划组织支球队参加,安排场比赛,则为( )A、 B、 C、 D、13. 如图,在矩形中, , , 以点为圆心,长为半径画弧,交于点 , 连接 , 则扇形的面积为( )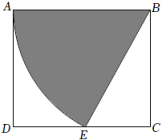 A、 B、 C、 D、14. 如图,在中,平分 , 于点 , , 若 , , 则的值为( )
A、 B、 C、 D、14. 如图,在中,平分 , 于点 , , 若 , , 则的值为( ) A、 B、 C、 D、15. 在中, , , , 为边一点且 , 若过点作直线截 , 使截得的三角形与原三角形相似,则满足条件的直线有( )A、条 B、条 C、条 D、条16. 如图, , 分别是反比例函数和在第一象限内的图象,点和点在上,线段交于点 , 线段交于点下列结论中正确的为( )
A、 B、 C、 D、15. 在中, , , , 为边一点且 , 若过点作直线截 , 使截得的三角形与原三角形相似,则满足条件的直线有( )A、条 B、条 C、条 D、条16. 如图, , 分别是反比例函数和在第一象限内的图象,点和点在上,线段交于点 , 线段交于点下列结论中正确的为( ) A、 B、 C、为中点 D、
A、 B、 C、为中点 D、二、填空题:本题共3小题,共10分。
-
17. 方程有两个相等的实数根,则的值为 .18. 如图所示,小区内有个圆形花坛 , 点在弦上, , , , 则这个花坛的半径为 .
 19. 如图,菱形的边与轴平行,点的横坐标为 , , 反比例函数的图象经过 , 两点.
19. 如图,菱形的边与轴平行,点的横坐标为 , , 反比例函数的图象经过 , 两点. (1)、点的横坐标为;(2)、菱形的面积是 .
(1)、点的横坐标为;(2)、菱形的面积是 .三、解答题:本题共7小题,共68分。解答应写出文字说明,证明过程或演算步骤。
-
20.(1)、解方程;(2)、计算 .21. 已知某蓄电池的电压为定值,使用该蓄电池时,电流单位:与电阻单位:是反比例函数关系,它的图象如图所示.
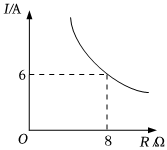 (1)、求出这个反比例函数的解析式;(2)、如果以此蓄电池为电源的用电器限制电流不能超过 , 求出用电器可变电阻应控制在什么范围.22. 为测量图中的铁塔的高度,小明利用自制的测角仪在点测得塔顶的仰角为 , 从点向正前方行进米到处,再用测角仪在点测得塔顶的仰角为已知测角仪的高度为米,求铁塔的高度 .
(1)、求出这个反比例函数的解析式;(2)、如果以此蓄电池为电源的用电器限制电流不能超过 , 求出用电器可变电阻应控制在什么范围.22. 为测量图中的铁塔的高度,小明利用自制的测角仪在点测得塔顶的仰角为 , 从点向正前方行进米到处,再用测角仪在点测得塔顶的仰角为已知测角仪的高度为米,求铁塔的高度 . 23. 小明的口袋中有把相似的钥匙,其中只有把钥匙能打开教室前门锁,但他忘了是哪两把钥匙.(1)、小明从口袋中随机摸出一把钥匙就能打开门锁的概率是;(2)、小明随机摸出两把钥匙,其中一把能打开另一把不能打开门锁请用树状图的方法,求出这个事件的概率.24. 如图,是的直径,点在直径上与 , 不重合 , 且 , 连接 , 与交于点 , 在上取一点 , 使与相切.
23. 小明的口袋中有把相似的钥匙,其中只有把钥匙能打开教室前门锁,但他忘了是哪两把钥匙.(1)、小明从口袋中随机摸出一把钥匙就能打开门锁的概率是;(2)、小明随机摸出两把钥匙,其中一把能打开另一把不能打开门锁请用树状图的方法,求出这个事件的概率.24. 如图,是的直径,点在直径上与 , 不重合 , 且 , 连接 , 与交于点 , 在上取一点 , 使与相切.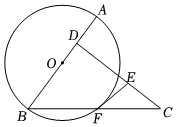 (1)、求证:;(2)、若是的中点, , 求的长.25. 某超市销售品牌的纯牛奶,进价是元箱根据前段时间的销售经验,每天的售元箱与销售量箱有如下关系:
(1)、求证:;(2)、若是的中点, , 求的长.25. 某超市销售品牌的纯牛奶,进价是元箱根据前段时间的销售经验,每天的售元箱与销售量箱有如下关系:每箱售价元
每天销量箱
已知与之间的函数关系是一次函数.
(1)、求与的函数解析式;(2)、若该超市每天销售这种纯牛奶盈利元,要使顾客获得实惠,每箱售价是多少元?(3)、销售价格不能低于元箱,不能高于元箱,请你直接写出当品牌的纯牛奶的销售价格定为多少元箱时,超市一天的总盈利最大.26. 如图 , 抛物线与轴交于点 , 与轴交于点 . (1)、求抛物线的函数表达式.(2)、如图 , 当点从点匀速运动到点时,过点作交抛物线于点 , 交直线于点 , 连结求的最大值.(3)、若点从点匀速运动到点时,点恰好从点运动到点 , 作点关于直线的对称点 , 当点落在的一条边上时,请直接写出的长度.
(1)、求抛物线的函数表达式.(2)、如图 , 当点从点匀速运动到点时,过点作交抛物线于点 , 交直线于点 , 连结求的最大值.(3)、若点从点匀速运动到点时,点恰好从点运动到点 , 作点关于直线的对称点 , 当点落在的一条边上时,请直接写出的长度.