河北省沧州市青县2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-04-01 类型：期末考试

进入出卷网下载

一、选择题（1--6每小题3分，7--16每小题2分，共38分）

1. 以下四个图片中的物品，没有利用到三角形的稳定性的是（）

A、 B、 C、 D、

查看试题解析
2. 在实数范围内 $\frac{a^{2}}{a + 1}$ 有意义，则a的取值范围是（）

A、 $a = 0$ B、 $a = 1$ C、 $a \neq - 1$ D、 $a \neq 0$

查看试题解析
3. 已知：如图，∠1＝∠2，则不一定能使△ABD≌△ACD的条件是（）

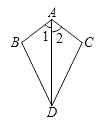A、AB＝AC B、BD＝CD C、∠B＝∠C D、∠BDA＝∠CDA

查看试题解析
4. 若 $☆ \times 3 m n = 3 m^{2} n^{3}$ ，则☆代表的代数式是（）

A、 $m n$ B、 $3 m n$ C、 $m n^{2}$ D、 $m^{2} n$

查看试题解析
5. 在 $△ A B C$ 中， $A C = A D = B D$ ， $∠ B = 25 °$ ，则 $∠ D A C =$ （）

A、 $50 °$ B、 $75 °$ C、 $80 °$ D、 $100 °$

查看试题解析
6. 已知等腰三角形的两边长 $a ， b$ 满足 $| a - 2 | + b^{2} - 10 b + 25 = 0$ ，那么这个等腰三角形的周长为（）

A、8 B、 $12$ C、9或 $12$ D、9

查看试题解析
7. 一张四边形纸片剪去一个角后，内角和将（）

A、减少180° B、不变 C、增加180° D、以上都有可能

查看试题解析
8. 下列是一位同学在课堂小测中做的四道题，如果每道题10分，满分40分，那么他的测试成绩是（）
（1） $π^{0} = 1$
（2） $(x + 2)^{2} = x^{2} + 4$
（3） $(- x + 2) (- x - 2) = x^{2} - 4$
（4） $- 8 a^{2} b^{3} \div 2 a b^{2} = - 4 a b$

A、40分 B、30分 C、20分 D、10分

查看试题解析
9. 新型的环保材料石墨烯是世界上最薄的纳米材料，科学家计算的其理论厚度是a米，用科学记数法表示为 $9.8 \times 1 0^{- 6}$ 米，则a中小数点后面0的个数为（）

A、4 B、5 C、6 D、7

查看试题解析
10. 如图，在 $∠ M O N$ 中，以点O为圆心，适当长为半径画弧，交 $O M$ 于点A，交 $O N$ 于点B，分别以点 $A ， B$ 为圆心，以大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧交于点C，画射线 $O C$ ，过点C作 $C D ⊥ O M$ 于点D，且 $C D = 2.5$ ，点E是射线 $O N$ 上一点，则 $C E$ 的长度不可能是（）

A、2 B、2.5 C、3 D、5

查看试题解析
11. 化简 $\frac{m^{2} - 3 m}{9 - m^{2}}$ 的结果是（）

A、 $\frac{m}{m + 3}$ B、 $- \frac{m}{m + 3}$ C、 $\frac{m}{m - 3}$ D、 $\frac{m}{3 - m}$

查看试题解析
12. 把正八边形 $A B C D E F G H$ 沿对角线 $A D$ 折叠，使点 $B$ 、 $C$ 落在正八边形内部的点 $M$ 、 $N$ 处，经过探究，嘉嘉说： $B A ⊥ A M$ ；娜娜说： $D N ∥ E F$ ；玲玲说：若连接 $N G$ ，则 $∠ G N M + ∠ D N M = 180 °$ ，则下列说法正确的是（）

A、只有嘉嘉和娜娜正确 B、只有嘉嘉说的正确 C、三个同学说的都正确 D、无法判断

查看试题解析
13. 劳动课上，八（1）班同学分成两组练习包饺子，女生组包300个饺子与男生组包200个所用的时间相同，已知女生组每分钟比男生组多包30个，若设女生组每分钟包 $x$ 个，则可列方程为（）

A、 $\frac{300}{x} = \frac{200}{x - 30}$ B、 $\frac{300}{x} = \frac{200}{x + 30}$ C、 $\frac{300}{x - 30} = \frac{200}{x}$ D、 $\frac{300}{x + 30} = \frac{200}{x}$

查看试题解析
14. 如果 $a x^{2} - 2 x + \frac{1}{2} = {(2 x - \frac{1}{2})}^{2} + b$ ，则 $a$ ， $b$ 的值是（）

A、2，0 B、4，0 C、2， $\frac{1}{4}$ D、4， $\frac{1}{4}$

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ A B C = 50 °$ ， $∠ C = 30 °$ ，作 $B D$ 平分 $∠ A B C$ 交边 $A C$ 于D，过A作 $A E ⊥ B D$ 于E，延长 $A E$ 交边 $B C$ 于点F，连接 $D F$ ，则 $∠ C D F$ 的度数为（）

A、 $50 °$ B、 $60 °$ C、 $65 °$ D、 $70 °$

查看试题解析
16. 如图，在平面直角坐标系中，射线 $O M$ 和x轴形成的角是 $30 °$ ，且点 $A_{1} ， A_{2} ， A_{3}$ …在x轴上，点 $B_{1} ， B_{2} ， B_{3}$ …在射线 $O M$ 上，若 $△ A_{1} B_{1} A_{2} ， △ A_{2} B_{2} A_{3} ， △ A_{3} B_{3} A_{4}$ …均为等边三角形，且点 $A_{1} (1 ， 0)$ ，则 $A_{2024}$ 的横坐标是（）

A、 $2^{2023}$ B、 $2^{2022}$ C、 $4046$ D、 $2023$

查看试题解析

二、填空题（每空2分，共10分）

17. 点 $A (- 4 ， 3)$ 关于x轴的对称点的坐标是．

查看试题解析
18. 已知甲图是边长为a的正方形，乙图是边长为b（ $a > b$ ）的正方形，丙图是长为a，宽为b的长方形，若先将乙图放在甲图的内部得到图（1），图（1）阴影部分的面积是4；再将甲乙两图并列摆放，以甲乙两图的边长之和为新的边长构造大正方形图（2），它的面积是100，则甲图的面积是，乙图的面积是．

查看试题解析
19. 如图，在 $△ A B C$ 中， $∠ B = 60 ° ， A B = 20 ， B C = 35$ ，动点D从点B出发，以每秒2个单位长度的速度匀速向点A移动，同时点E从点C出发以每秒3个单位长度的速度匀速向点B移动，当D、E两点中有一点到达终点时，两点同时停止运动，设点D的运动时间为t秒．

(1)、若 $△ D B E$ 为等边三角形，则 $t =$ ．

(2)、若 $△ D B E$ 为直角三角形，则 $t =$ ．

查看试题解析

三、解答题（共72分）

20. 分解因式与解方程：

(1)、 ${(2 a - b)}^{2} + 8 a b$ ；

(2)、 $\frac{2}{x - 2} + \frac{x + 1}{2 - x} = 2$ ．

查看试题解析
21. 在日历上，我们会发现其中某些数满足的一些规律，如图甲是2024年元月份的日历．我们任意选择其中所示的方框部分，将每个方框部分中4个位置上的数交叉相乘，再相减，例如：
$3 \times 9 - 2 \times 10 = 27 - 20 = 7$ ，
$19 \times 25 - 18 \times 26 = 475 - 468 = 7$ ，
不难发现结果都是7．

(1)、如图乙是2024年2月份的日历，在图乙中类似的部分试一试，看看是否存在同样的规律；

(2)、设某一类似部分最左上角的数字为x，请你利用整式的运算对以上的规律加以证明．

查看试题解析
22. 如图，在平面直角坐标系中， $A (0 ， 3)$ ， $B (- 2 ， 1)$ ， $C (3 ， 2)$ ．

(1)、在图中作出 $△ A B C$ 关于y轴对称的 $△ A^{'} B^{'} C^{'}$ ．

(2)、点 $C^{'}$ 的坐标为； $△ A^{'} B^{'} C^{'}$ 的面积为．

(3)、在x轴上找出一点P，使得 $P A + P B$ 的值最小．（不写作法，保留作图痕迹）

查看试题解析
23. 嘉嘉学习了等腰三角形，知道“等边对等角”，他想：那么边不相等时，它们所对的角有什么样的关系呢？于是他做了如下探索：
他剪了一个如图所示的 $△ A B C$ ，其中 $A B > A C$ ，然后把纸片折叠，使得 $A B$ 与 $A C$ 重合，且点B落在 $A C$ 延长线上的 $B_{1}$ 处，然后利用轴对称和外角的性质得到三角形中边角的不等关系．

(1)、请你完成证明过程：
证明：由轴对称的性质可以得到 $△ A B D ≌ △ A B_{1} D$
∴    ▲         $= ∠ B_{1}$ （          ）
又∵ $∠ A C B$ 是 $△ D C B_{1}$ 的一个外角
∴ $∠ A C B = ∠ B_{1} + ∠ B_{1} D C$ （            ）
∴ $∠ A C B >$     ▲
即 $∠ A C B > ∠ B$ （等量代换）
∴在 $△ A B C$ 中，若 $A B > A C$ ，则 $∠ A C B > ∠ B$

(2)、请用（1）的结论解决问题：在 $△ D E F$ 中，若 $D E > D F$ ， $D G$ 是 $E F$ 边上的中线，请探索 $∠ E D G$ 和 $∠ F D G$ 的大小关系，并写出证明的过程．（温馨提示：延长 $D G$ 到点H，使 $G H = D G$ ，连接 $F H$ ）

查看试题解析
24. 以下是佳佳同学化简 $(\frac{x + 2}{x^{2} - 2 x} - \frac{x - 1}{x^{2} - 4 x + 4}) \div \frac{x - 4}{x}$ 的运算过程的一部分，请仔细观察并回答问题：
解：原式= $[\frac{x + 2}{x (x - 2)} - \frac{x - 1}{{(x - 2)}^{2}}] \div \frac{x - 4}{x}$ ---------------------①
= $[\frac{(x + 2) {(x - 2)}^{}}{x {(x - 2)}^{2}} - \frac{x (x - 1)}{x {(x - 2)}^{2}}] \div \frac{x - 4}{x}$ ------------------②
= $\frac{x^{2} - 4 - x^{2} - x}{x {(x - 2)}^{2}} \times \frac{x}{x - 4}$ -------------------------------③
．．．．．．

(1)、在上面佳佳同学的运算过程中，从第步开始出错；

(2)、请你写出完整的解答过程，若x的值满足 $x^{2} - 4 x - 6 = 0$ ，求原式的值．

查看试题解析
25. 国家推行“节能减排，低碳经济”政策后，新能源汽车比较畅销，“平安行”4S店在甲厂家花240万元订购一批A品牌新能源汽车，在乙厂家花450万元购进一批B品牌新能源汽车，若所购B品牌新能源汽车数量是A品牌新能源汽车的2倍，且每辆的进价比A品牌便宜5000元．

(1)、求A、B品牌新能源车每辆的进价分别是多少万元？

(2)、如果两批汽车按相同的标价销售，最后的5辆汽车在元旦大促销，顾客在享受了各种优惠政策后，相当于九四折优惠购车，要使两批新能源汽车全部售完后利润不低于 $30 %$ （不考虑其他因素），那么每辆新能源汽车的标价至少是多少万元？

查看试题解析
26. 如图

(1)、问题情境：如图，等腰 $R t △ A B C$ ， D是斜边 $B C$ 上一点，连接 $A D$ ，在AD右侧作 $A F ⊥ A D$ ，且 $A F = A D$ ， $A E$ 平分 $∠ D A F$ 交边 $B C$ 于点E，连接 $E F$ 和 $C F$ ，请直接写出线段 $B E 、 C F 、 E F$ 的关系：；

(2)、猜想验证：若 D是斜边 $B C$ 上一动点，且 $A E$ 平分 $∠ D A F$ 交边 $B C$ 于点E，其他条件不变，此时上面的结论是否还成立，请说明理由．

(3)、拓展延伸：若点D运动到斜边 $C B$ 的延长线上， $A E$ 平分 $∠ D A F$ 交边 $B C$ 于点E，其他条件不变，请直接写出线段 $B E 、 C F 、 E F$ 的关系：．

查看试题解析

河北省沧州市青县2023-2024学年八年级上学期期末数学试题

一、选择题（1--6每小题3分，7--16每小题2分，共38分）

二、填空题（每空2分，共10分 ）

三、解答题（共72分）

二、填空题（每空2分，共10分）