河北省沧州市孟村县2023-2024学年七年级上学期期末数学试卷
试卷更新日期:2024-04-01 类型:期末考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 已知有理数、在数轴上的位置如图所示,下列结论正确的是( )
 A、 B、 C、 D、2. 下列各式运用等式的性质变形,正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则3. 已知x-2y=3,则代数式6-2x+4y的值为( )A、0 B、-1 C、-3 D、34. 如图,数轴上一动点向左移动个单位长度到达点 , 再向右移动个单位长度到达点若点表示的数为 , 则与点表示的数互为相反数的是( )
A、 B、 C、 D、2. 下列各式运用等式的性质变形,正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则3. 已知x-2y=3,则代数式6-2x+4y的值为( )A、0 B、-1 C、-3 D、34. 如图,数轴上一动点向左移动个单位长度到达点 , 再向右移动个单位长度到达点若点表示的数为 , 则与点表示的数互为相反数的是( ) A、 B、 C、 D、5. 某公司去年10月份的利润为a万元,11月份比10月份减少5%,12月份比11月份增加了9%,则该公司12月份的利润为( )
A、 B、 C、 D、5. 某公司去年10月份的利润为a万元,11月份比10月份减少5%,12月份比11月份增加了9%,则该公司12月份的利润为( )
A、(a-5%)(a+9%)万元 B、(a-5%+9%)万元 C、a(1-5%+9%)万元 D、a(1-5%)(1+9%)万元6. 有理数 , , , 按从小到大的顺序排列是( )A、 B、 C、 D、7. 观察下列算式:, , , , , , , , , 根据上述算式中的规律,你认为的末位数字是( )
A、 B、 C、 D、8. 观察图 , 若天平保持平衡,在图天平的右盘中需放入个才能使其平衡.( ) A、 B、 C、 D、9. 如图,点在直线上,过作射线 , , 一直角三角板的直角顶点与点重合,边与重合,边在直线的下方若三角板绕点按每秒的速度沿逆时针方向旋转一周,在旋转的过程中,第秒时,直线恰好平分锐角 , 则的值为( )
A、 B、 C、 D、9. 如图,点在直线上,过作射线 , , 一直角三角板的直角顶点与点重合,边与重合,边在直线的下方若三角板绕点按每秒的速度沿逆时针方向旋转一周,在旋转的过程中,第秒时,直线恰好平分锐角 , 则的值为( ) A、 B、 C、或 D、或10. 如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A、 B、 C、或 D、或10. 如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( ) A、y=2n+1 B、y=2n+n C、y=2n+1+n D、y=2n+n+1
A、y=2n+1 B、y=2n+n C、y=2n+1+n D、y=2n+n+1二、填空题:本题共4小题,共15分。
-
11. 一列火车匀速行驶,经过一条长300m的隧道需要20s的时间.隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10s.设火车的长度为xm. 列方程.12. 如图是一个计算程序,若输入a的值为-1,则输出的结果应为.
 13. 一副三角板按如图方式摆放,若 , 则的度数为 , 只用度表示的补角为 .
13. 一副三角板按如图方式摆放,若 , 则的度数为 , 只用度表示的补角为 . 14. 小师和小滨进行了十次剪刀石头布的对决,已知:小师出了次石头,次剪刀,次布;小滨出了次石头,次剪刀,次布;次中没有平局;你不知道她们的出拳顺序则这次对决中赢者是 .
14. 小师和小滨进行了十次剪刀石头布的对决,已知:小师出了次石头,次剪刀,次布;小滨出了次石头,次剪刀,次布;次中没有平局;你不知道她们的出拳顺序则这次对决中赢者是 .三、解答题:本题共5小题,共55分。解答应写出文字说明,证明过程或演算步骤。
-
15. 计算:(1)、;(2)、16. 解方程 .17. 若代数式的值与字母的取值无关,求代数式的值.18. 钟表是我们日常生活中常用的计时工具如图,在圆形钟面上,把一周等分成个大格,每个大格等分成个小格,分针和时针均绕中心匀速转动本题中的角均指小于的角 ,
 (1)、分针每分钟转度,时针每分钟转度,当时间为:时,分针和时针的夹角为度;(2)、求:开始后几分钟分针第一次追上时针;(3)、点为点钟的位置,平分 , 平分 , 从:开始计时,分钟后 , , 求的值.19. 数轴上点表示 , 点表示 , 点表示点表示如图,将数轴在原点和点、处各折一下,得到一条“折线数轴”在“折线数轴”上,把两点所对应的两数之差的绝对值叫这两点间的和谐距离例如,点和点在折线数轴上的和谐距离为个单位长度,动点从点出发,以个单位秒的速度沿着折线数轴的正方向运动,从点运动到点期间速度变为原来的一半,过点后继续以原来的速度向终点运动;点从点出发的同时,点从点出发,一直以个单位秒的速度沿着“折线数轴”负方向向终点运动,其中一点到达终点时,两点都停止运动设运动的时间为秒.
(1)、分针每分钟转度,时针每分钟转度,当时间为:时,分针和时针的夹角为度;(2)、求:开始后几分钟分针第一次追上时针;(3)、点为点钟的位置,平分 , 平分 , 从:开始计时,分钟后 , , 求的值.19. 数轴上点表示 , 点表示 , 点表示点表示如图,将数轴在原点和点、处各折一下,得到一条“折线数轴”在“折线数轴”上,把两点所对应的两数之差的绝对值叫这两点间的和谐距离例如,点和点在折线数轴上的和谐距离为个单位长度,动点从点出发,以个单位秒的速度沿着折线数轴的正方向运动,从点运动到点期间速度变为原来的一半,过点后继续以原来的速度向终点运动;点从点出发的同时,点从点出发,一直以个单位秒的速度沿着“折线数轴”负方向向终点运动,其中一点到达终点时,两点都停止运动设运动的时间为秒.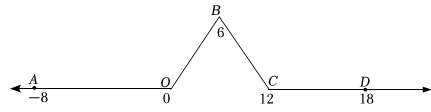 (1)、当秒时,、两点在折线数轴上的和谐距离为;(2)、当点、都运动到折线段上时,、两点间的和谐距离 用含有的代数式表示;、两点间的和谐距离 用含有的代数式表示: 时,、两点相遇;(3)、求当为多少秒时,、两点在折线数轴上的和谐距离为个单位长度.
(1)、当秒时,、两点在折线数轴上的和谐距离为;(2)、当点、都运动到折线段上时,、两点间的和谐距离 用含有的代数式表示;、两点间的和谐距离 用含有的代数式表示: 时,、两点相遇;(3)、求当为多少秒时,、两点在折线数轴上的和谐距离为个单位长度.