河北省邯郸市经济技术开发区2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-04-01 类型:期末考试
一、选择题(16个小题,每题3分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 实数 , , , , , 中无理数有( )A、5个 B、4个 C、3个 D、2个2. 式子有意义,则实数a的取值范围是( )A、 B、 C、且 D、且3. 如图,由图案(1)到图案(2)再到图案(3)的变化过程中,不可能用到的图形变换是( )
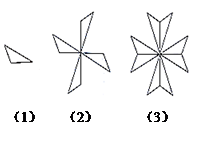 A、轴对称 B、旋转 C、中心对称 D、平移4. 的平方根是x , 的立方根是y , 则的值为( )A、 B、0 C、0或 D、6或5. 下面是马小虎的答卷,他的得分应是( )
A、轴对称 B、旋转 C、中心对称 D、平移4. 的平方根是x , 的立方根是y , 则的值为( )A、 B、0 C、0或 D、6或5. 下面是马小虎的答卷,他的得分应是( )姓名马小虎得分?
判断题每小题分,共分
代数式 , 是分式
当时,分式无意义
不是最简分式
若分式的值为 , 则的值为
分式中 , 的值均扩大为原来的倍,分式的值保持不变A、分 B、分 C、分 D、分6. 下列说法正确的是( )A、1.8和1.80的精确度相同 B、5.7万精确到0.1 C、6.610精确到千分位 D、0.12349精确到0.001是0.1247. 我们可以用反证法来证明“在一个三角形中,至少有一个内角小于或等于”.下面写出了证明该问题过程中的四个步骤:①这与“三角形的内角和等于”这个定理矛盾.②所以在一个三角形中,至少有一个内角小于或等于 . ③假设三角形没有一个内角小于或等于 , 即三个内角都大于 . ④则三角形的三个内角的和大于 . 这四个步骤正确的顺序是( )A、①②③④) B、③④②① C、③④①② D、④③②①8. 如图,点C在线段上,且 , , , , 下列说法错误的是( ) A、 B、 C、 D、9. 如图,面积为3的正方形的顶点在数轴上,且表示的数为 , 以点为圆心,长为半径画圆,交数轴于点 . 则点所表示的数为( )
A、 B、 C、 D、9. 如图,面积为3的正方形的顶点在数轴上,且表示的数为 , 以点为圆心,长为半径画圆,交数轴于点 . 则点所表示的数为( ) A、 B、 C、 D、10. 如图,已知 . 根据下列作图回答问题:①作射线;②以O为圆心,以任意长为半径画弧,分别交于点C、D;③以为圆心,以长为半径画弧,交于点;④以点为圆心,长为半径画弧,与第③步中所画的弧相交于点;④过点画射线 , 则 , 这种做法正确的理由是( )
A、 B、 C、 D、10. 如图,已知 . 根据下列作图回答问题:①作射线;②以O为圆心,以任意长为半径画弧,分别交于点C、D;③以为圆心,以长为半径画弧,交于点;④以点为圆心,长为半径画弧,与第③步中所画的弧相交于点;④过点画射线 , 则 , 这种做法正确的理由是( ) A、由可得 , 进而可证 B、由可得 , 进而可证 C、由可得 , 进而可证 D、由“等边对等角”可得11. 在计算时,嘉嘉和琪琪使用方法不同,但计算结果相同,则( )
A、由可得 , 进而可证 B、由可得 , 进而可证 C、由可得 , 进而可证 D、由“等边对等角”可得11. 在计算时,嘉嘉和琪琪使用方法不同,但计算结果相同,则( )嘉嘉:
琪琪:
A、嘉嘉正确 B、琪琪正确 C、都正确 D、都不正确12. 设的小数部分为a , 则的值为( )A、22 B、 C、 D、13. 如图,在等腰中, , , D是边的中点,E是边(端点除外)上的动点,过点D作的垂线交边于点F . 下列结论错误的是( ) A、 B、 C、四边形的面积等于面积的一半 D、14. 如图,在和中,点 , , 在同一条直线上, , , 若 , , 则的长为( )
A、 B、 C、四边形的面积等于面积的一半 D、14. 如图,在和中,点 , , 在同一条直线上, , , 若 , , 则的长为( ) A、8 B、6 C、4 D、215. 如图,矩形内有两个相邻的白色正方形,其面积分别为2和18,则图中阴影部分的面积为( )
A、8 B、6 C、4 D、215. 如图,矩形内有两个相邻的白色正方形,其面积分别为2和18,则图中阴影部分的面积为( )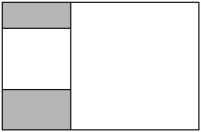 A、 B、 C、4 D、616. 如图,在中,的角平分线与的垂直平分线交于点D , 于点E , , 交的延长线于点F . 若 , , 则的长为( )
A、 B、 C、4 D、616. 如图,在中,的角平分线与的垂直平分线交于点D , 于点E , , 交的延长线于点F . 若 , , 则的长为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(四个小题,17-18每题3分,19-20每题4分,共14分)
-
17. 若与最简二次根式可以合并,则 .18. 如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧交于点M、N , 作直线 , 交于点 , 交于点 , 连接 , 若 , , , 则的周长为 .
 19. 已知关于x的分式方程的解是正数,则m的取值范围是20. 如图,将绕点旋转一定角度得到 , , , , 则的长度是 .
19. 已知关于x的分式方程的解是正数,则m的取值范围是20. 如图,将绕点旋转一定角度得到 , , , , 则的长度是 .
三、解答题(6道题,共58分.解答应写出文字说明、证明过程或演算步骤)
-
21. 已知:的平方根是与 , 且的算术平方根是3.(1)、求的值;(2)、求的立方根.22. 已知:如图 , , . 求证: .
 23. 已知 , .(1)、求的值;(2)、求 .24. 如图,已知点在的内部,且点与点关于对称,交于点 , 点与点关于对称,交于点分别交于点 .
23. 已知 , .(1)、求的值;(2)、求 .24. 如图,已知点在的内部,且点与点关于对称,交于点 , 点与点关于对称,交于点分别交于点 . (1)、连接 , 若 , 求的周长;(2)、若 , 求证:平分 .
(1)、连接 , 若 , 求的周长;(2)、若 , 求证:平分 .
