云南省保山市腾冲市2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-04-01 类型：期末考试

进入出卷网下载

一、单选题（本大题共12小题，每小题只有一个正确选项，每小题3分，共36分）

1. 下列关于体育的图形中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算结果正确的是（）

A、 ${(a^{3})}^{3} = a^{6}$ B、 ${(- a b^{4})}^{2} = a^{2} b^{8}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
3. 如图，将长方形ABCD沿AE折叠，得到如图所示的图形，已知 $∠ C E F = 50 °$ ，则 $∠ A E D$ 的度数是（）

A、40° B、50° C、65° D、76°

查看试题解析
4. 把分式 $\frac{x y}{x + 3 y}$ 中的x和y都扩大10倍，分式的值（）

A、扩大10倍 B、扩大100倍 C、不变 D、缩小10倍

查看试题解析
5. 计算： $3 x^{2} y \cdot (- 4 x y^{4})$ 的结果是（）

A、 $7 x^{2} y^{4}$ B、 $- 7 x^{3} y^{5}$ C、 $12 x^{2} y^{4}$ D、 $- 12 x^{3} y^{5}$

查看试题解析
6. 正十二边形的外角和为（）

A、360° B、1080° C、1440° D、1800°

查看试题解析
7. 如图，已知 $∠ A = 36 °$ ， $∠ A D C = 100 °$ ， $B E ⊥ A C$ 于点E ，则 $∠ B$ 的度数为（）

A、44° B、46° C、40° D、36°

查看试题解析
8. 如图，△ABC中边AB的垂直平分线分别交BC、AB于点D、E ， BE＝3cm，△ADC的周长为9cm，则△ABC的周长是（）

A、10cm B、12cm C、14cm D、15cm

查看试题解析
9. 下列等式从左到右的变形，属于因式分解的是（）

A、 $(a + 4) (a - 4) = a^{2} - 16$ B、 $x^{2} - 4 y^{2} = (x + 4 y) (x - 4 y)$ C、 $x^{2} - 2 x + 1 = x (x - 1) + 1$ D、 $x^{2} - 8 x + 16 = {(x - 4)}^{2}$

查看试题解析
10. 如图，为了促进当地旅游发展，某地要在三条公路AB、AC、BC两两相交围成的一块平地上修建一个度假村，要使这个度假村到三条公路的距离相等，应选择的位置是（）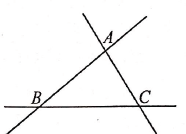

A、△ABC三边垂直平分线的交点 B、△ABC三条中线的交点 C、△ABC三个内角角平分线的交点 D、△ABC三条高的交点

查看试题解析
11. 随着生活水平的提高和环保意识的增强，小亮家购置了新能源电动汽车，这样他乘电动汽车比乘公交车上班所需的时间少用了15分钟，已知电动汽车的平均速度是公交车的2.5倍，小亮家到上班地点的距离为8千米．若设乘公交车平均每小时走x千米，则可列方程为（）

A、 $\frac{8}{x} + 15 = \frac{8}{2.5 x}$ B、 $\frac{8}{x} = \frac{8}{2.5 x} + 15$ C、 $\frac{8}{x} + \frac{1}{4} = \frac{8}{2.5 x}$ D、 $\frac{8}{x} = \frac{8}{2.5 x} + \frac{1}{4}$

查看试题解析
12. 如图所示，图1是一个边长为a的正方形剪去一个边长为b的小正方形，图2是一个边长为a的正方形剪去一个长为a ，宽为b的长方形．若图1、图2中阴影部分的面积分别记为 $S_{1}$ 、 $S_{2}$ ， $a > b > 0$ ，设 $k = \frac{S_{1}}{S_{2}}$ ，则有（）

A、 $0 < k < \frac{1}{2}$ B、 $1 < k < 2$ C、 $\frac{1}{2} < k < 1$ D、 $k > 2$

查看试题解析

二、填空题（本大题共4小题，每小题2分，共8分）

13. 香包刺绣又称陇绣，是一项传统技艺．绣线多采用产地范围生产的蚕丝线、棉线、麻线等，织成蚕丝线的蚕丝截面可近似地看成圆，直径约为 $10 μ m$ ，蚕丝线的截面面积约为0.000000785cm^2.其中数据0.000000785用科学记数法可表示为．

查看试题解析
14. 如图， $△ A B C ≌ △ D E C$ ，点B的对应点E在线段AB上， $∠ B = 70 °$ ，则∠DCA的度数是．

查看试题解析
15. 如图，已知 $B A = B C$ ，要使 $△ A B D ≌ △ C B D$ 全等，则应添加的条件是．

查看试题解析
16. 若分式 $\frac{x}{x - 3}$ 有意义，则 $x$ 的取值范围是.

查看试题解析

三、解答题（本大题共8小题，共56分）

17.

(1)、 ${(\frac{1}{2})}^{- 2} + {(- 1)}^{2024} + | - 2 | - {(π - 3.14)}^{0}$

(2)、 $(x - 3) (3 + x) - {(1 - x)}^{2} + 2 (5 - x)$

查看试题解析
18. 先化简，再求值．
$\frac{x^{2} - 8 x + 16}{x^{2} + 2 x} \div (\frac{6}{x + 2} - 1)$ ，其中x选取－2，0，1，4中的一个合适的数．

查看试题解析
19. 如图，点C是线段AB的中点，∠B＝∠ACD ， $A D / / C E$ ．
求证： $△ A C D ≌ △ C B E$

查看试题解析
20. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点的坐标分别为A（－3，4），B（－4，1），C（－1，2）．

(1)、作出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ （点A、B、C的对应点分别为点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ ），并直接写出点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 的坐标；

(2)、点P在y轴上，使得△BCP的周长最小，作出点P ．（不写作法，保留作图痕迹）

查看试题解析
21. 如图，在△ABC中，∠ABC＝60°，BE平分∠ABC ， AD为BC边上的高，若∠BEC＝75°，求∠DAC的度数．

查看试题解析
22. 先仔细阅读材料，再尝试解决问题：
通过对实数的学习，我们知道 $x^{2} \geq 0$ ，根据完全平方公式： ${(a \pm b)}^{2} = a^{2} \pm 2 a b + b^{2}$ ，所以完全平方公式的值为非负数，这一性质在数学中有着广泛的应用，比如探求多项式 $2 x^{2} + 8 x - 3$ 的最小值时，我们可以这样处理：
解：原式 $= 2 (x^{2} + 4 x) - 3 = 2 (x^{2} + 2 x \cdot 2 + 2^{2} - 2^{2}) - 3 = 2 {(x + 2)}^{2} - 11$
∵ $2 {(x + 2)}^{2} \geq 0$
∴ $2 {(x + 2)}^{2} - 11 \geq 0 - 11$ ，且当 $(x = - 2)$ 时， $2 {(x + 2)}^{2} - 11$ 的最小，为 $- 11$ ；
请根据上面的解题思路，求多项式 $3 x^{2} - 6 x + 4$ 的最小值是多少，并写出对应的x的值．

查看试题解析
23. 某公司会计欲查询乙商品的每件进价（如下表），发现进货单已被墨水污染．
商品
进价（元/件）
数量（件）
总金额
甲
7200
乙
3200
李师傅：我记得甲商品数量比乙商品的数量多50%．
王师傅：我记得甲商品进价比乙商品进价每件高20元．
请同学们帮该公司求出甲、乙两商品的数量分别是多少件？

查看试题解析
24. 问题背景：我们学习等边三角形时得到直角三角形的一个性质：在直角三角形中，如果一个锐角等于 $30 °$ ，那么它所对的直角边等于斜边的一半，即：如图①在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A B C = 30 °$ ，则 $A C = \frac{1}{2} A B$ ．
探究结论：小明同学对以上结论作了进一步研究．

(1)、如图①，作AB边上的中线CE ，得到结论：① $△ A C E$ 为等边三角形；②BE与CE之间的数量关系为；

(2)、如图②，CE是△ABC的中线，点D是边CB上任意一点，连接AD ，作等边△ADP ，且点P在∠ACB的内部，连接BP ．试探究线段BP与DP之间的数量关系，写出你的猜想并加以证明；

(3)、如图③，当点D为边CB延长线上任意一点时，在（2）中条件的基础上，线段BP与DP之间存在怎样的数量关系？直接写出答案即可．

查看试题解析

商品	进价（元/件）	数量（件）	总金额
甲			7200
乙			3200