云南省保山市腾冲市2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-04-01 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，每小题只有一个正确选项，每小题3分，共36分）

1. 2023年10月26日，神州十七号载人飞船发射任务圆满成功．下列航天图标是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件是随机事件的是（）

A、平行四边形的对角相等，邻角互补． B、方程 $a x^{2} - x = 0$ 是关于 $x$ 的一元二次方程． C、任意画一个三角形，其内角和为 $360 °$ ． D、两个负数相乘，积是正数．

查看试题解析
3. 如图， $A B$ 是 $⊙ O$ 的直径， $C$ 是 $⊙ O$ 上一点（ $A ， B$ 除外）， $∠ C = 25 °$ ，则 $∠ B O D$ 的度数是（）

A、50° B、65° C、25° D、130

查看试题解析
4. 平面直角坐标系中，点 $P$ 的坐标为 $(- 1 ， 2)$ ，则 $P$ 点关于原点 $O$ 对称的点 $Q$ 的坐标为（）

A、 $(2 ， - 1)$ B、 $(1 ， - 2)$ C、 $(- \sqrt{5} ， - 1)$ D、 $(- 2 ， - 1)$

查看试题解析
5. 如图，在 $△ A B C$ 中，点 $D$ ， $E$ 是边 $A B$ ， $A C$ 的中点，若 $△ A D E$ 的面积为1，则四边形 $B D E C$ 的面积为（）

A、1 B、2 C、4 D、3

查看试题解析
6. 一元二次方程 $3 x^{2} - 4 x + 1 = 0$ 的根的情况是（）

A、有相等的两个实数根 B、没有实数根 C、有不相等的两个实数根 D、无法判断

查看试题解析
7. 函数 $y = \frac{2}{x}$ 的图象位于（）

A、第一象限、第三象限 B、第二象限、第四象限 C、第一象限 D、第二象限

查看试题解析
8. 如图，以点 $O$ 为位似中心， $△ A B C$ 与 $△ A_{1} B_{1} C_{1}$ 位似，且相似比为 $1 ： 2$ ，则 $△ A B C$ 与 $△ A_{1} B_{1} C_{1}$ 周长的比是（）

A、 $1 ： 9$ B、 $1 ： 4$ C、 $1 ： 3$ D、 $1 ： 2$

查看试题解析
9. 抛物线 $y = 3 (x + 2)^{2} + 3$ 的顶点坐标是（）

A、 $(- 2 ， 3)$ B、 $(2 ， - 3)$ C、 $(- 2 ， - 3)$ D、 $(2 ， 3)$

查看试题解析
10. 已知 $⊙ O$ 的半径为8cm，点 $M$ 到圆心 $O$ 的距离为10cm，则点 $M$ 和 $⊙ O$ 的位置关系是（）

A、点 $M$ 在 $⊙ O$ 内 B、点 $M$ 在 $⊙ O$ 上 C、点 $M$ 在 $⊙ O$ 外 D、无法判断

查看试题解析
11. 某地区为贯彻“绿水青山就是金山银山”理念，在2022年植树造林2000亩，计划2024年植树造林2880亩．若设植树造林面积的年平均增长率为 $x$ ，则 $x$ 的值为（）

A、20% B、11% C、10% D、120%

查看试题解析
12. 如图是二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的一部分，对称轴是直线 $x = - 2$ ，关于下列结论：① $a b < 0$ ；② $b^{2} - 4 a c > 0$ ；③ $a - b + c < 0$ ；④ $b - 4 a = 0$ ；⑤方程 $a x^{2} + b x = 0$ 的两个根为 $x_{1} = 0 ， x_{2} = - 4$ ．其中正确的结论有（）

A、①③④ B、②③⑤ C、①②⑤ D、②④⑤

查看试题解析

二、填空题（本大题共4小题，每小题2分，共8分）

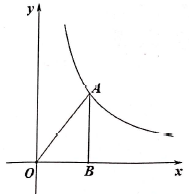
13. 抛物线 $y = x^{2} - 2 x$ 的对称轴是．

查看试题解析
14. 在一个不透明的袋子中，有白色棋子和黑色棋子共20颗，这些棋子除颜色外均相同，将袋中的棋子搅匀，从中随机摸出一颗棋子，记下颜色后再放回袋子中，不断重复这一过程，摸了100次后，发现有60次摸到黑色棋子，请你估计这个袋子中黑色棋子有颗．

查看试题解析
15. 如图，在平面直角坐标系 $x O y$ 中，点 $A$ 在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上，过点 $A$ 作 $A B ⊥ x$ 于点 $B$ ，若 $S_{△ A O B} = 12$ ，则 $k$ 的值为．

查看试题解析
16. 如图， $A B$ 是 $⊙ O$ 的弦，半径 $O A = 30 c m$ ， $∠ A O B = 120 °$ ，则 $△ A O B$ 的面积为 $c m^{2}$ ．

查看试题解析

三、解答题（本大题共8小题，共56分）

17. 解方程 $- 2 x^{2} + x + 3 = 0$

查看试题解析
18. 如图，在平行四边形 $A B C D$ 中，点 $N$ 在 $B C$ 上，连接 $D N$ ，点 $M$ 在 $D N$ 上，连接 $A M$ ，且 $∠ A M N = ∠ B$ ．求证： $△ A D M ∽ △ D N C$ ．

查看试题解析
19. 某校计划举办“学习二十大”演讲比赛，确定了“5G时代”、“北斗卫星”、“高铁速度”、“绿色低碳”四个主题，将其制成四张背面看上去无差别的卡片（如图所示），并把卡片背面朝上洗匀．

(1)、若小丽随机抽取一张卡片，则她选中的主题是“绿色低碳”的概率是；

(2)、若小英从卡片中随机抽取一张卡片确定主题后，将卡片放回洗匀，小亮再随机从中抽取一张卡片确定主题，请用列表或画树状图的方法求出他们恰好抽取不同主题的概率．（用对应的字母表示）

查看试题解析
20. 如图，在平面直角坐标系中， $R t △ A B C$ 的三个顶点坐标分别是 $A (- 3 ， 2)$ ， $B (0 ， 4)$ ， $C (0 ， 2)$ ．

(1)、将 $△ A B C$ 以点 $O$ 为旋转中心旋转180°，画出旋转后对应的 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 的坐标；

(2)、在 $x$ 轴上找一点 $P$ （保作图留痕迹），使得 $P A + P B$ 的值最小，请直接写出点 $P$ 的坐标．

查看试题解析
21. 如图所示，已知 $A (- 4 ， n)$ ， $B (2 ， - 4)$ ，是一次函数 $y = k x + b$ 和反比例函数 $y = \frac{m}{x}$ 的图象的两个交点．

(1)、求一次函数和反比例函数的解析式；

(2)、一次函数的图象与 $y$ 轴交与点 $C$ ，求 $△ A O B$ 的面积．

查看试题解析
22. 进入秋冬季节，空气干燥．某电器商城准备购进一批加湿器，每台进价为80元，经市场调查，售价定为100元/台，每天可售出500台，售价每增加1元，每天的销售量将减少10台，设每台加湿器的售价增加 $x$ 元．

(1)、设每天的销售量为 $y$ 台，直接写出 $y$ 与 $x$ 的函数关系式；

(2)、用含 $x$ 的代数式表示该商城每天销售该加湿器所获得的利润 $W$ 元，并计算若要获利最大，则每台加湿器的售价应定为多少元？获得的最大利润是多少元？

查看试题解析
23. 如图，在 $△ A B C$ 中， $A O$ 平分 $∠ B A C$ 交 $B C$ 于点 $O$ ，以点 $O$ 为圆心， $B O$ 长为半径的 $⊙ O$ 与 $A B$ 相切于点 $B$ ，与 $B C$ 相交于点 $D$ ．

(1)、求证： $A C$ 是 $⊙ O$ 的切线；

(2)、若 $A B = 5 ， A C = 13$ ，设 $△ A B O$ 的面积为 $S_{1}$ ， $△ A B C$ 的面积为 $S_{2}$ ， $m = \frac{S_{1}}{S_{2}}$ ．求常数 $m$ 的值．

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，直线 $A B$ 的函数表达式为 $y = a x - 2 a$ （ $a \neq 0$ ， $a$ 为常数），点 $A 、 B$ 分别在 $y$ 轴和 $x$ 轴上，且 $O A = 2 O B$ ，点 $A$ 关于 $x$ 轴的对称点为 $C$ ，点 $B$ 关于 $y$ 轴的对称点为 $D$ ，以点 $C$ 为顶点的拋物线经过点 $D$ ．

(1)、求点 $A ， B$ 的坐标；

(2)、求抛物线的解析式；

(3)、在（2）中拋物线的对称轴上有一点 $P$ ，且以点 $D 、 O 、 P$ 为顶点的三角形与 $△ A O B$ 相似，求出所有满足条件的点 $P$ 的坐标．

查看试题解析