湖南省长沙市宁乡市2023-2024学年八年级上学期数学期末考试试卷

试卷更新日期：2024-04-01 类型：期末考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 平面直角坐标系中，点 $P (2，3)$ 关于 $x$ 轴对称的点的坐标是（）

A、 $(2，3)$ B、 $(- 2，3)$ C、 $(2 ， - 3)$ D、 $(- 2 ， - 3)$

查看试题解析
2. 在下列长度的 $4$ 条线段中，能与长 $5 c m$ ， $8 c m$ 的两条线段围成一个三角形的是（）

A、 $2 c m$ B、 $3 c m$ C、 $10 c m$ D、 $13 c m$

查看试题解析
3. 下列分式是最简分式的是（）

A、 $\frac{4 m}{6 n}$ B、 $\frac{a + b}{a^{2} - b^{2}}$ C、 $\frac{x - y}{x^{2} - y^{2}}$ D、 $\frac{x + y}{x^{2} + y^{2}}$

查看试题解析
4. 如图，工人师傅设计了一种测零件内径AB的卡钳，卡钳交叉点O为AA'、BB'的中点，只要量出A'B'的长度，就可以知道该零件内径AB的长度．依据的数学基本事实是（）

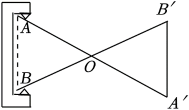A、两边及其夹角分别相等的两个三角形全等 B、两角及其夹边分别相等的两个三角形全等 C、两条直线被一组平行线所截，所得的对应线段成比例 D、两点之间线段最短

查看试题解析
5. 下列运算正确的是（）

A、 $a^{2} \cdot a = a^{2}$ B、 $(a^{3})^{2} = a^{6}$ C、 $(a b)^{2} = a b^{2}$ D、 $(a + b)^{2} = a^{2} + b^{2}$

查看试题解析
6. 一个正多边形的内角和为 $540 °$ ，则这个正多边形的每一个内角是（）

A、 $120 °$ B、 $108 °$ C、 $90 °$ D、 $60$

查看试题解析
7. 如图，方格纸中的 $∠ 1$ 和 $∠ 2$ 的大小关系是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 2 = 2 ∠ 1$ C、 $∠ 2 = 90 ° + ∠ 1$ D、 $∠ 1 + ∠ 2 = 180 °$

查看试题解析
8. 如图，边长为 $(m + n)$ 的正方形纸片剪出一个边长为 $m$ 的正方形之后余下部分又剪开拼成个长方形 $($ 不重叠无缝隙 $)$ ，若拼成的长方形一边长为 $n$ ，则长方形的面积是（）

A、 $2 m + 2 n$ B、 $m + 2 n$ C、 $2 m^{2} + n$ D、 $2 m n + n^{2}$

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ A = 40 °$ ，分别以点 $A$ ， $C$ 为圆心，以适当的长度为半径画弧，过两弧的交点作直线交 $A B$ 于点 $D$ ，连接 $C D$ ；再如图所示作射线 $B P$ ，交 $C D$ 于点 $P .$ 根据图中尺规作图痕迹推断，以下结论错误的是（）

A、 $A D = C D$ B、 $∠ A B P = ∠ P B C$ C、 $∠ A B P = ∠ A$ D、 $∠ B P C = 115 °$

查看试题解析
10. “爱劳动，劳动美．”甲、乙两同学同时从家里出发，分别到距家 $6 k m$ 和 $10 k m$ 的实践基地参加劳动．若甲、乙的速度比是 $3$ ： $4$ ，结果甲比乙提前 $20 m i n$ 到达基地，求甲、乙的速度．设甲的速度为 $3 x k m / h$ ，则依题意可列方程为（）

A、 $\frac{6}{3 x} + \frac{1}{3} = \frac{10}{4 x}$ B、 $\frac{6}{3 x} + 20 = \frac{10}{4 x}$ C、 $\frac{6}{3 x} - \frac{10}{4 x} = \frac{1}{3}$ D、 $\frac{6}{3 x} - \frac{10}{4 x} = 20$

查看试题解析

二、填空题：本题共6小题，每小题3分，共18分。

11. 如图，自行车的车身为三角结构，这样做根据的数学道理是．

查看试题解析
12. 因式分解：2x²-2=.

查看试题解析
13. 若分式 $\frac{1}{2024 - x}$ 有意义，则字母 $x$ 需满足的条件是．

查看试题解析
14. 若 $3^{- n} = \frac{1}{27}$ ，则 $n =$ ．

查看试题解析
15. 如图： $A D$ 为 $△ A B C$ 的角平分线，且 $A B = 3$ ， $A C = 5$ ，则 $△ A B D$ 和 $△ A D C$ 的面积之比为．

查看试题解析
16. 如图， $O$ 是直线 $B C$ 上一点， $∠ A O B = 30 °$ ， $P O$ 平分 $∠ A O C$ ， $P M / / B C$ 交 $A O$ 于点 $M$ ， $M P = 10 c m$ ， $P D ⊥ O C$ 于点 $D$ ，则 $P D =$ $c m$ ．

查看试题解析

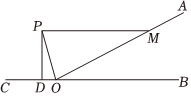
三、计算题：本大题共1小题，共6分。

17. 解分式方程： $\frac{x - 3}{x - 2} + 1 = \frac{3}{x - 2}$ ．

查看试题解析

四、解答题：本题共8小题，共66分。解答应写出文字说明，证明过程或演算步骤。

18. 计算： $(π - 2036)^{0} - (\frac{1}{2})^{- 2} + (\sqrt{3} - 1) (\sqrt{3} + 1) + (- 1)^{2024}$ ．

查看试题解析
19. 先化简，再求值： $(a - 3 b) (a + 3 b) + (a - 3 b)^{2}$ ，其中 $a = - 2 ， b = \frac{1}{2}$ ．

查看试题解析
20. 如图，点 $E$ 在 $△ A B C$ 外部，点 $D$ 在边 $B C$ 上， $D E$ 交 $A C$ 于点 $F$ ，若 $∠ 1 = ∠ 2 = ∠ 3$ ， $A B = A D$ ，

求证：

(1)、 $∠ E = ∠ C$ ；

(2)、 $B C = D E$ ．

查看试题解析
21. 某化工厂为了给员工创建安全的工作环境，采用 $A$ ， $B$ 两种机器人来搬运化工原料 $.$ 其中 $A$ 型机器人比 $B$ 型机器人每小时多搬运 $30$ 千克， $A$ 型机器人搬运 $1500$ 千克所用时间与 $B$ 型机器人搬运 $1000$ 千克所用时间相等．

(1)、求 $A$ ， $B$ 两种机器人每小时分别搬运多少千克化工原料；

(2)、若每台 $A$ 型， $B$ 型机器人的价格分别为 $5$ 万元和 $3$ 万元，该化工厂需要购进 $A$ ， $B$ 两种机器人共 $12$ 台，工厂现有资金 $45$ 万元，则最多可购进 $A$ 型机器人多少台？

查看试题解析
22. 如图， $△ A B C$ 三个顶点的坐标分别为 $A (1，1)$ 、 $B (4，2)$ 、 $C (3，5)$ ．

(1)、若 $△ A' B' C'$ 与 $△ A B C$ 关于 $x$ 轴成轴对称，作出 $△ A' B' C'$ ；

(2)、若 $P$ 为 $y$ 轴上一点，使得 $△ A P C$ 周长最小，在图中作出点 $P$ ，并写出 $P$ 点的坐标为；

(3)、计算 $△ A B C$ 的面积．

查看试题解析
23. 数学来源于生活，生活中处处有数学，用我们平时喝的糖水做“糖水实验”也能验证发现一些数学结论 $.$ 现有 $a$ 克糖水，其中含有 $b$ 克糖 $(a > b > 0)$ ，则糖水的浓度 $($ 即糖的质量与糖水的质量比 $)$ 为 $\frac{b}{a}$ ．

(1)、糖水实验一：加入 $m$ 克水，则糖水的浓度为 $.$ 生活经验告诉我们，糖水加水后会变淡，由此可以写出一个不等式，我们趣称为“糖水不等式”．

(2)、糖水实验二：
将“糖水实验一”中的“加入 $m$ 克水”改为“加入 $m$ 克糖”，则糖水的浓度为 $.$ 根据生活经验，请你写出一个新的“糖水不等式” ．

(3)、请结合 $(2)$ 探究得到的结论尝试证明：
设 $a$ 、 $b$ 、 $c$ 为 $△ A B C$ 三边的长，求证： $\frac{c}{a + b} + \frac{a}{b + c} + \frac{b}{a + c} < 2$ ．

查看试题解析
24. 学习代数式求值时，遇到这样一类题“代数式 $2 y - m x + 5 + 3 x + y - 8$ 的值与 $x$ 的取值无关，求 $m$ 的值”，通常的解题方法是：把 $x$ ， $y$ 看作字母， $m$ 看作系数合并同类项，因为代数式的值与 $x$ 的取值无关，所以含 $x$ 的系数为 $0$ ，即原式 $= (3 - m) x + 3 y - 3$ ，所以 $3 - m = 0$ ，则 $m = 3$ ．

(1)、若多项式 $(3 x - 2) a - 2 x + a^{2}$ 的值与 $x$ 的取值无关，求 $a$ 的值；

(2)、如图 $1$ 的小长方形，长为 $a$ ，宽为 $b$ ，按照图 $2$ 方式不重叠地放在大长方形 $A B C D$ 内，大长方形中未被覆盖的两个部分 $($ 图中阴影部分 $)$ ，设左上角的面积为 $S_{1}$ ，右下角的面积为 $S_{2}$ ，当 $A B$ 的长变化时， $2 S_{1} - S_{2}$ 的值始终保持不变，请求出 $a$ 与 $b$ 的数量关系．

查看试题解析
25.

(1)、动手操作：如图 $①$ ，将矩形纸片 $A B C D$ 折叠，使点 $D$ 与点 $B$ 重合，点 $C$ 落在点 $C'$ 处，折痕为 $E F$ ，若 $∠ A B E = 20 °$ ，那么 $∠ D E F$ 度数为；

(2)、观察发现：小明将三角形纸片 $A B C (A B > A C)$ 沿过点 $A$ 的直线折叠，使得 $A C$ 落在 $A B$ 边上，折痕为 $A D$ ，展开纸片 $($ 如图 $②)$ ；再次折叠该三角形纸片，使点 $A$ 和点 $D$ 重合，折痕为 $E F$ ，展平纸片后得到 $△ A E F ($ 如图 $③) .$ 小明认为 $△ A E F$ 是等腰三角形，你同意吗？请说明理由；

(3)、实践运用：将矩形纸片 $A B C D$ 按如下步骤操作：将纸片对折得折痕 $E F$ ，折痕与 $A D$ 边交于点 $E$ ，与 $B C$ 边交于点 $F$ ；将矩形 $A B F E$ 与矩形 $E F C D$ 分别沿折痕 $M N$ 和 $P Q$ 折叠，使点 $A$ 、点 $D$ 都与点 $F$ 重合，展开纸片，此时恰好有 $M P = M N = P Q ($ 如图 $④)$ ，求 $∠ M N F$ 的大小．

查看试题解析