湖南省衡阳市城区2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-04-01 类型:期末考试
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 要使二次根式有意义,则实数的取值范围是( )A、 B、 C、 D、2. 已知实数在数轴上的对应点位置如图,则化简的结果是( )
 A、 B、 C、 D、3. 关于的一元二次方程化为一般形式后不含一次项,则的值为( )A、 B、 C、 D、4. 如图,在平面直角坐标系中,的顶点都在格点上,如果将沿轴翻折,得到 , 那么点的对应点的坐标为( )
A、 B、 C、 D、3. 关于的一元二次方程化为一般形式后不含一次项,则的值为( )A、 B、 C、 D、4. 如图,在平面直角坐标系中,的顶点都在格点上,如果将沿轴翻折,得到 , 那么点的对应点的坐标为( )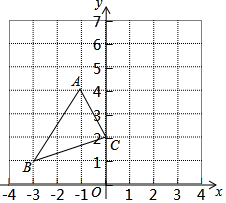 A、 B、 C、 D、5. 已知 , 是方程的两根,则的值为( )A、 B、 C、 D、6. 如图,若 , 则下列各式错误的是( )
A、 B、 C、 D、5. 已知 , 是方程的两根,则的值为( )A、 B、 C、 D、6. 如图,若 , 则下列各式错误的是( )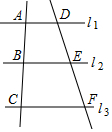 A、 B、 C、 D、7. 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M,C两点间的距离为( )
A、 B、 C、 D、7. 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M,C两点间的距离为( ) A、0.5km B、0.6km C、0.9km D、1.2km8. 小亮是一名职业足球队员,根据以往比赛数据统计,小亮进球率为 ,他明天将参加一场比赛,下面几种说法正确的是( )A、小亮明天的进球率为 B、小亮明天每射球10次必进球1次 C、小亮明天有可能进球 D、小亮明天肯定进球9. 如图,一艘潜水艇在海面下米的点处发现其正前方的海底处有黑匣子,同时测得黑匣子的俯角为 , 潜水艇继续在同一深度直线航行米到点处,测得黑匣子的俯角为 , 则黑匣子所在的处距离海面的深度是( )
A、0.5km B、0.6km C、0.9km D、1.2km8. 小亮是一名职业足球队员,根据以往比赛数据统计,小亮进球率为 ,他明天将参加一场比赛,下面几种说法正确的是( )A、小亮明天的进球率为 B、小亮明天每射球10次必进球1次 C、小亮明天有可能进球 D、小亮明天肯定进球9. 如图,一艘潜水艇在海面下米的点处发现其正前方的海底处有黑匣子,同时测得黑匣子的俯角为 , 潜水艇继续在同一深度直线航行米到点处,测得黑匣子的俯角为 , 则黑匣子所在的处距离海面的深度是( ) A、米 B、米 C、米 D、米10. 如图,能使∽成立的条件是( )
A、米 B、米 C、米 D、米10. 如图,能使∽成立的条件是( )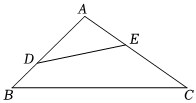 A、 B、 C、 D、11. 如图,四边形 和 是以点 为位似中心的位似图形,若 ,四边形 的面积为9 ,则四边形 的面积为( )
A、 B、 C、 D、11. 如图,四边形 和 是以点 为位似中心的位似图形,若 ,四边形 的面积为9 ,则四边形 的面积为( ) A、15 B、25 C、18 D、2712. 我们已经学习了利用配方法解一元二次方程,其实配方法还有其它重要应用.
A、15 B、25 C、18 D、2712. 我们已经学习了利用配方法解一元二次方程,其实配方法还有其它重要应用.
例:已知可取任何实数,试求二次三项式的值的范围.
解:
.
无论取何实数,总有 , .
即无论取何实数,的值总是不小于的实数.
问题:已知可取任何实数,则二次三项式的最值情况是( )A、有最大值 B、有最小值 C、有最大值 D、有最小值二、填空题:本题共6小题,每小题3分,共18分。
-
13. 若最简二次根式是同类二次根式,则的值为 .14. 一元二次方程的解为 .15. 已知关于的方程有两个不相等的实数根,则的取值范围是 .16. 如图,在四边形中, , , 分别是 , 的中点,已知 , , 则 .
 17. 如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2米,BP=3米,PD=12米,那么该古城墙的高度CD是米.
17. 如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2米,BP=3米,PD=12米,那么该古城墙的高度CD是米. 18. “健康荆州,你我同行”,市民小张积极响应“全民健身动起来”号召,坚持在某环形步道上跑步.已知此步道外形近似于如图所示的 , 其中 , 与间另有步道相连,地在正中位置,地与地相距若 , , 小张某天沿路线跑一圈,则他跑了 .
18. “健康荆州,你我同行”,市民小张积极响应“全民健身动起来”号召,坚持在某环形步道上跑步.已知此步道外形近似于如图所示的 , 其中 , 与间另有步道相连,地在正中位置,地与地相距若 , , 小张某天沿路线跑一圈,则他跑了 .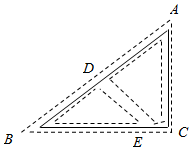
三、解答题:本题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤。
-
19. 计算:
(1)、;
(2)、 .20. 解方程: .21. 如图,在中,为边上一点, . (1)、求证:;(2)、若 , , 求的长.22. 我市某中学举行“法制进校园”知识竞赛,赛后将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图.请你根据统计图解答下列问题.
(1)、求证:;(2)、若 , , 求的长.22. 我市某中学举行“法制进校园”知识竞赛,赛后将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图.请你根据统计图解答下列问题.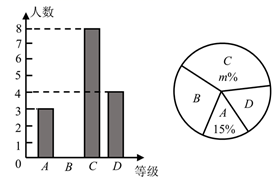 (1)、成绩为“B等级”的学生人数有名;(2)、在扇形统计图中,表示“D等级”的扇形的圆心角度数为 , 图中m的值为;(3)、学校决定从本次比赛获得“A等级”的学生中选出2名去参加市中学生知识竞赛.已知“A等级”中有1名女生,请用列表或画树状图的方法求出女生被选中的概率.23. 某淘宝网店销售台灯,每个台灯售价为60元,每星期可卖出300个,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30个.已知该款台灯每个成本为40元,(1)、若每个台灯降x元( ),则每星期能卖出个台灯,每个台灯的利润是元.(2)、在顾客得实惠的前提下,该淘宝网店还想获得6480元的利润,应将每件的售价定为多少元?24. 阅读以下材料,并按要求完成相应的任务.
(1)、成绩为“B等级”的学生人数有名;(2)、在扇形统计图中,表示“D等级”的扇形的圆心角度数为 , 图中m的值为;(3)、学校决定从本次比赛获得“A等级”的学生中选出2名去参加市中学生知识竞赛.已知“A等级”中有1名女生,请用列表或画树状图的方法求出女生被选中的概率.23. 某淘宝网店销售台灯,每个台灯售价为60元,每星期可卖出300个,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30个.已知该款台灯每个成本为40元,(1)、若每个台灯降x元( ),则每星期能卖出个台灯,每个台灯的利润是元.(2)、在顾客得实惠的前提下,该淘宝网店还想获得6480元的利润,应将每件的售价定为多少元?24. 阅读以下材料,并按要求完成相应的任务.
构建几何图形解决代数问题是“数形结合”思想的重要应用,例如:在计算时,可构造如图所示的图形在中, , , 设 , 延长至点 , 使得 , 连结 , 易知 , , 所以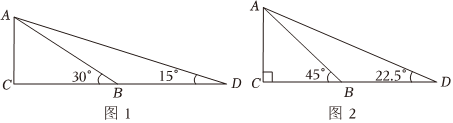
任务:(1)、请根据上面的步骤,完成的计算;(2)、请类比这种方法,计算图中的值.

