湖南重点大学附中2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-04-01 类型:期末考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
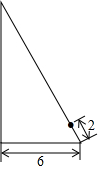
1. 我国古代数学家祖冲之推算出的近似值为 , 它与的误差小于将用科学记数法可以表示为( )A、 B、 C、 D、2. 下列三个分式 , , 的最简公分母是( )A、 B、 C、 D、3. 下列式子中,是最简二次根式的是( )A、 B、 C、 D、4. 若 , 则的值是( )A、 B、 C、 D、5. 化简的结果是( ).A、 B、 C、 D、6. 如图,点所表示的数是( )
 A、 B、 C、 D、7. 若成立,则满足得条件( )A、 B、 C、 D、8. 已知命题;若 , 则;若 , 则;两个全等的三角形的面积相等;三条边对应相等的两个三角形全等上述命题的逆命题为真命题的个数是( )A、 B、 C、 D、9. 若关于的分式方程的解为非负数,则的取值范围是( )A、且 B、且
A、 B、 C、 D、7. 若成立,则满足得条件( )A、 B、 C、 D、8. 已知命题;若 , 则;若 , 则;两个全等的三角形的面积相等;三条边对应相等的两个三角形全等上述命题的逆命题为真命题的个数是( )A、 B、 C、 D、9. 若关于的分式方程的解为非负数,则的取值范围是( )A、且 B、且
C、且 D、且10. 已知 , 则的值是( )A、 B、 C、 D、二、填空题:本题共6小题,每小题3分,共18分。
-
11. 在实数范围内分解因式: .12. 已知 , , 则 .13. 若在实数范围内有意义,则的取值范围是 .14. 若 , 则 .15. 如图,小明想知道学校旗杆的高度,他将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端处,发现此时绳子底端距离打结处 , 则旗杆的高度为
 16. “赵爽弦图”是我国古代数学的瑰宝,在如图所示的弦图中,大正方形是由四个全等的直角三角形和一个小正方形组成的若 , , 则的面积为 .
16. “赵爽弦图”是我国古代数学的瑰宝,在如图所示的弦图中,大正方形是由四个全等的直角三角形和一个小正方形组成的若 , , 则的面积为 .
三、解答题:本题共8小题,共67分。解答应写出文字说明,证明过程或演算步骤。
-
17. 计算: .18. 先化简,再求值: , 其中 .19. 如图,在△ABC中,AD⊥BC于D,AB=3,BD=2,DC=1,求AC的值.
 20. 已知: , .(1)、求的值.(2)、求的值.21. 如图,公路和公路在点处交汇,且 , 在处有一所中学,米,此时有一辆消防车在公路上沿方向以每秒米的速度行驶,假设消防车行驶时周围米以内有噪音影响.
20. 已知: , .(1)、求的值.(2)、求的值.21. 如图,公路和公路在点处交汇,且 , 在处有一所中学,米,此时有一辆消防车在公路上沿方向以每秒米的速度行驶,假设消防车行驶时周围米以内有噪音影响. (1)、学校是否会受到影响?请说明理由.(2)、如果受到影响,则影响时间是多长?22. 有两款售价相同的汽车,信息如下表所示:
(1)、学校是否会受到影响?请说明理由.(2)、如果受到影响,则影响时间是多长?22. 有两款售价相同的汽车,信息如下表所示:燃油车
新能源汽车
油箱容积:升
电池容量:千瓦时
油价:元升
电价:元千瓦时
续航里程:千米
续航里程:千米
每千米行驶费用:元
每千米行驶费用:____元
(1)、新能源车的每千米行驶费用是元;用含的代数式表示
(2)、若燃油车的每千米行驶费用比新能源车多元.
分别求出这两款车的每千米行驶费用;
若燃油车和新能源车每年的其他费用分别为元和元,则每年行驶里程在什么范围时,新能源车的年费用更低?年费用年行驶费用年其它费用23. 如图,在中, , 垂足为 , 平分交于点 , , , . (1)、求证:;(2)、求点到边的距离.24. 压轴题
(1)、求证:;(2)、求点到边的距离.24. 压轴题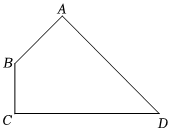 (1)、已知 , , 为的三边长,且有试判断的形状并加以证明.(2)、已知 , 满足 , 且 , 都是整数,求的值.(3)、在平面直角坐标系中,已知点 , , 在轴上求一点 , 使得是等腰三角形,求点的坐标画图,在图上标出坐标
(1)、已知 , , 为的三边长,且有试判断的形状并加以证明.(2)、已知 , 满足 , 且 , 都是整数,求的值.(3)、在平面直角坐标系中,已知点 , , 在轴上求一点 , 使得是等腰三角形,求点的坐标画图,在图上标出坐标
(4)、如图,在四边形中, , , , , 在、上分别找一点、 , 使得的周长最小,求周长的最小值.(5)、我们定义:如果两个多项式与的和为常数,则称与互为“对消多项式”,这个常数称为它们的“对消值”如与互为“对消多项式”,它们的“对消值”为已知关于的多项式与互为“对消多项式”,“对消值”为若 , , 求代数式的最小值.