湖南省永州市双牌县2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-04-01 类型:期末考试
一、选择题(本大题共10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂到答题卡上相应的位置)
-
1. 如果分式 有意义,那么x的取值范围是( )A、全体实数 B、 C、 D、2. 如果 , 那么的值等于( )A、 B、 C、12 D、213. 已知x≠0,则等于( )A、 B、 C、 D、4. 实数a , b在数轴上的位置如图所示,那么化简的结果是( )
 A、 B、b C、 D、5. 下列各式比较大小正确的是( )A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 不等式组 的解集在以下数轴表示中正确的是( )A、
A、 B、b C、 D、5. 下列各式比较大小正确的是( )A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 不等式组 的解集在以下数轴表示中正确的是( )A、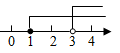 B、
B、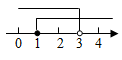 C、
C、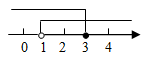 D、
D、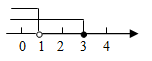 8. 下列命题是假命题的是( )A、有一个角是60°的等腰三角形是等边三角形 B、等边三角形有3条对称轴 C、有两边和一角对应相等的两个三角形全等 D、线段垂直平分线上的点到线段两端的距离相等9. 如图,在中, , AE是的角平分线,点D是AE上的一点,则下列结论错误的是( )
8. 下列命题是假命题的是( )A、有一个角是60°的等腰三角形是等边三角形 B、等边三角形有3条对称轴 C、有两边和一角对应相等的两个三角形全等 D、线段垂直平分线上的点到线段两端的距离相等9. 如图,在中, , AE是的角平分线,点D是AE上的一点,则下列结论错误的是( ) A、 B、 C、 D、10. 甲、乙两人加工一批零件,甲完成120个与乙完成100个所用的时间相同,已知甲比乙每天多完成4个.设甲每天完成x个零件,依题意下面所列方程正确的是( )A、 = B、 = C、 = D、 =
A、 B、 C、 D、10. 甲、乙两人加工一批零件,甲完成120个与乙完成100个所用的时间相同,已知甲比乙每天多完成4个.设甲每天完成x个零件,依题意下面所列方程正确的是( )A、 = B、 = C、 = D、 =二、填空题(本大题共8个小题,每小题3分,共24分。请将正确答案填在答题卡上相应的位置)
-
11. 当时,分式 .12. 不等式 的正整数解为.13. 计算 =14. 目前科学家发现一种新型病毒的直径为0.0000251米,用科学记数法表示该病毒的直径为米.15. 若a , b为实数,且 , 则的值 .16. 如图,在△ABC中,∠A=35°,∠B=90°,线段AC的垂直平分线MN与AB交于点D,与AC交于点E,则∠BCD=度.
 17. 现定义一种新的运算: . 例如: , 则不等式的解集为 .18. 如图,在和中, , 以点D为顶点作 , 两边分别交AB , AC于点M , N , 连接MN , 则的周长为 .
17. 现定义一种新的运算: . 例如: , 则不等式的解集为 .18. 如图,在和中, , 以点D为顶点作 , 两边分别交AB , AC于点M , N , 连接MN , 则的周长为 .
三、解答题(本大题共8个小题,共66分。解答题要求写出证明步骤或解答过程)
-
19. 计算: .20. 解分式方程:21. 已知 , 求的值.22. 解不等式组: ,并把此不等式组的解集在数轴上表示出来.23. 先化简,再求值: , 其中 .24. 如图,在中,AB边垂直平分线a交BC于点D , AC边的垂直平分线b交BC于点E , a , b相交于点O , 连接AD , AE , 的周长为12厘米.
 (1)、请作AB边垂直平分线a和AC边的垂直平分线b , 并把图形补充完整(不写做法,保留痕迹).(2)、求BC的长.(3)、分别连接OA , OB , OC , 若的周长为26厘米,求OA的长.25. 永州市在进行“六城同创”的过程中,决定购买A , B两种树对某路段进行绿化改造,若购买A种树3棵,B种树4棵,需要3200元;购买A种树5棵,B种树2棵,需要3000元.(1)、求购买A , B两种树每棵各需多少元?(2)、考虑到绿化效果,购进A种树不能少于48棵,且用于购买这两种树的资金不低于45000元.若购进这两种树共100棵.问有哪几种购买方案?26. [阅读理解]课外兴趣小组活动时,老师提出了如下问题:
(1)、请作AB边垂直平分线a和AC边的垂直平分线b , 并把图形补充完整(不写做法,保留痕迹).(2)、求BC的长.(3)、分别连接OA , OB , OC , 若的周长为26厘米,求OA的长.25. 永州市在进行“六城同创”的过程中,决定购买A , B两种树对某路段进行绿化改造,若购买A种树3棵,B种树4棵,需要3200元;购买A种树5棵,B种树2棵,需要3000元.(1)、求购买A , B两种树每棵各需多少元?(2)、考虑到绿化效果,购进A种树不能少于48棵,且用于购买这两种树的资金不低于45000元.若购进这两种树共100棵.问有哪几种购买方案?26. [阅读理解]课外兴趣小组活动时,老师提出了如下问题:如图1,在中,若 , 求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:如图2,延长AD到点E , 使 , 连结BE , 请根据小明的方法思考:
图1
 图2
图2  图3
图3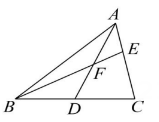 (1)、由已知和作图能得到 , 其理由是什么?(2)、求AD的取值范围.(3)、如图3,AD是的中线,BE交AC于点F , 且 , 试说明 .
(1)、由已知和作图能得到 , 其理由是什么?(2)、求AD的取值范围.(3)、如图3,AD是的中线,BE交AC于点F , 且 , 试说明 .