湖南省长沙市雅礼教育集团2023-2024学年七年级上学期数学期末考试试卷

试卷更新日期：2024-04-01 类型：期末考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。

1. “两岸猿声啼不住，轻舟已过万重山”.2023年8月29日，华为搭载自研麒麟芯片的mate60系列低调开售．据统计，截至2023年10月21日，华为mate60系列手机共售出约160万台，将数据1600000用科学记数法表示应为（）

A、 $0.16 \times 1 0^{7}$ B、 $1.6 \times 1 0^{6}$ C、 $1.6 \times 1 0^{7}$ D、 $16 \times 1 0^{6}$

查看试题解析
2. 下列图形能折叠成圆锥的是（）

A、 B、 C、 D、

查看试题解析
3. 下面的计算正确的是（）

A、 $2 a - a = 2$ B、 $a + 2 a^{2} = 2 a^{3}$ C、 $5 (a + b) = 5 a + b$ D、 $- (a - b) = - a + b$

查看试题解析
4. 下列说法错误的是（）

A、 $a b + 1$ 是二次二项式 B、 $0$ 是单项式 C、 $- x y^{2}$ 的系数是 $- 1$ D、 $- 2^{2} a b^{2}$ 的次数是 $5$

查看试题解析
5. 下列方程变形正确的是（）

A、由 $3 x + 2 = 4 x - 1$ ，得 $3 x + 4 x = 2 - 1$ B、由 $5 x = 8$ ，得 $x = \frac{5}{8}$ C、由 $\frac{y}{2} = 0$ ，得 $y = 0$ D、由 $\frac{x}{5} - 2 = 1$ ，得 $x - 2 = 5$

查看试题解析
6. 下列图形中，由 $∠ 1 = ∠ 2$ 能判定 $A B / / C D$ 的是（）

A、 B、 C、 D、

查看试题解析
7. 一份数学试卷共 $20$ 道选择题，每道题都给出了 $4$ 个选项，其中只有一个正确选项，每道题选对得 $5$ 分，不选或错选倒扣 $2$ 分，已知小雅得了 $65$ 分，设小雅选对了 $x$ 道题，则下列所列方程正确的是（）

A、 $2 x + 5 (20 - x) = 65$ B、 $5 x + 2 (20 - x) = 65$ C、 $5 x - 2 (20 - x) = 65$ D、 $5 x - 2 (20 + x) = 65$

查看试题解析
8. 下列说法中正确的是（）

A、不相交的两条直线叫做平行线
B、把弯曲的河道改直，能够缩短航程，这是由于两点之间，线段最短
C、射线 $A B$ 与射线 $B A$ 是同一条射线 D、线段 $A B$ 叫做 $A$ 、 $B$ 两点间的距离

查看试题解析
9. 如图，某海域有三个小岛 $A$ ， $B$ ， $O$ ，在小岛 $O$ 处观测到小岛 $A$ 在它的北偏东 $65 °$ 的方向上，观测到小岛 $B$ 在它的南偏西 $15 °$ 的方向上，则 $∠ A O B$ 的度数是（）

A、 $80 °$ B、 $100 °$ C、 $130 °$ D、 $140 °$

查看试题解析
10. 有理数 $a$ ， $b$ ， $c$ 在数轴上的位置如图，则 $| a + c | + | c - b | - | b - a | =$ （）

A、 $- 2 b$ B、 $0$ C、 $2 c$ D、 $2 c - 2 b$

查看试题解析

二、填空题：本题共6小题，每小题3分，共18分。

11. 如果向东 $50$ 米记作 $+ 50$ 米，那么向西 $10$ 米记作米 $.$

查看试题解析
12. 若代数式 $9 a^{3} b^{m}$ 与 $- 2 a^{n} b^{2}$ 是同类项，那么 $m n =$ ．

查看试题解析
13. 已知 $a + b = 8$ ，则代数式 $1 - 2 a - 2 b$ 的值为．

查看试题解析
14. 已知 $∠ α = 60 ° 16'$ ，则 $∠ α$ 补角是．

查看试题解析
15. 如图， $∠ A O B = ∠ C O D = 90 °$ ， $∠ A O D = 150 °$ ，则 $∠ B O C =$ 度 $.$

查看试题解析
16. 定义一种新运算 $\forall$ ：对任意有理数 $a$ ， $b$ 都有 $a \forall b = - a - b^{2}$ ，如 $2 \forall 3 = - 2 - 3^{2} = - 11$ ，则 $(2024 \forall 1) \forall 2 =$ ．

查看试题解析

三、解答题：本题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤。

17. 计算： $2 \div \frac{1}{3} + (- 2)^{3} - | 5 - 8 | + 4 \times (- 3)$ ．

查看试题解析
18. 解方程： $\frac{2 x - 1}{3} = \frac{3 x - 7}{5} - 1$ ．

查看试题解析
19. 先化简，再求值： $x^{2} - (2 x^{2} - 4 y) + 3 (x^{2} - y)$ ，其中 $x = 3$ ， $y = 2$ ．

查看试题解析
20. 已知 $a$ 、 $b$ 互为倒数， $c$ 、 $d$ 互为相反数， $| m | = 3$ ， $n$ 是最大的负整数，求代数式 $(- a b)^{2024} - 3 (c + d) - n + m^{2}$ 的值．

查看试题解析
21. 如图，点 $C$ 是线段 $A B$ 的中点，点 $D$ 是线段 $B C$ 的中点，线段 $B D = 3$ ．

(1)、求线段 $A B$ 的长；

(2)、如果点 $E$ 在线段 $A C$ 上，且 $E C = \frac{1}{3} A C$ ，求线段 $E D$ 的长．

查看试题解析
22. 某家具厂现有 $10$ 立方米木材，准备用来制作方桌，其中用部分木材制作桌面，其余木材制作桌腿 $.$ 已知制作一张方桌需要 $1$ 张桌面和 $4$ 条桌腿， $1$ 立方米木材可制作 $50$ 张桌面或 $300$ 条桌腿，要使制作出的桌面、桌腿恰好配套．

(1)、求制作桌面的木材和制作桌腿的木材分别为多少立方米？

(2)、若该家具厂的木材进货价为每立方米 $1500$ 元，制成方桌后 $($ 边角废料忽略不计 $)$ ，每张方桌的售价为 $150$ 元，则该家具厂制作的这批方桌全部售出后共获利多少元？

查看试题解析
23. 如图，直线 $E F$ 与 $C D$ 交于点 $O$ ， $O A$ 平分 $∠ C O E$ 交直线 $l$ 于点 $A$ ， $O B$ 平分 $∠ D O E$ 交直线 $l$ 于点 $B$ ，且 $∠ 1 + ∠ 2 = 90 °$ ．

(1)、求 $∠ A O B$ 的度数；

(2)、求证： $A B / / C D$ ；

(3)、若 $∠ 2$ ： $∠ 3 = 2$ ： $5$ ，求 $∠ A O F$ 的度数．

查看试题解析
24. 已知 $x_{0}$ 是关于 $x$ 的方程 $a x + b = 0 (a \neq 0)$ 的解， $y_{0}$ 是关于 $y$ 的方程 $c y + d = 0 (c \neq 0)$ 的解，若 $x_{0}$ ， $y_{0}$ 满足 $x_{0} + y_{0} = x_{0} y_{0}$ ，则称方程 $a x + b = 0 (a \neq 0)$ 与方程 $c y + d = 0 (c \neq 0)$ 互为“雅礼方程”；例如：方程 $x - 4 = 0$ 的解是 $x_{0} = 4$ ，方程 $4 y - y = 4$ 的解是 $y_{0} = \frac{4}{3}$ ，因为 $4 + \frac{4}{3} = 4 \times \frac{4}{3}$ ，所以方程 $x - 4 = 0$ 与方程 $4 y - y = 4$ 互为“雅礼方程”．

(1)、请判断方程 $x - 3 + 2 (x - 6) = 0$ 与方程 $y + 3 y = 5$ 是否互为雅礼方程 $.$ 并说明理由．

(2)、若关于 $x$ 的一元一次方程 $x - \frac{3 x - 2 a}{4} = a + \frac{3}{4} x$ 和关于 $y$ 的方程 $2 y - 3 = 1$ 互为“雅礼方程”，请求出 $a$ 的值．

(3)、关于 $x$ ， $y$ 的两个方程 $2 (x - 1) = 3 m - 2$ 与方程 $\frac{5 y + n}{2} - y = 2 n + 1$ ，若对于任何数 $m$ ，都使它们不是“雅礼方程”，求 $n$ 的值．

查看试题解析
25. 【材料阅读】
“数缺形时少直观，形少数时难入微”，数形结合是解决数学问题的重要思想方法．
如图 $1$ ，数轴上的点 $A$ 表示的数为 $a$ ， $B$ 表示的数为 $b$ ，且 $| a + 2 | + (b - 8)^{2} = 0 .$ 点 $C$ 是线段 $A B$ 的中点．

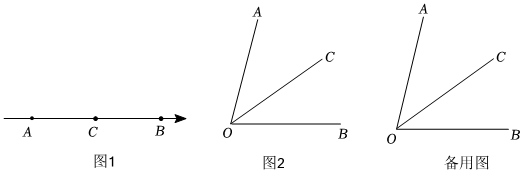(1)、点 $C$ 表示的数是；

(2)、若动点 $M$ 从点 $A$ 出发，以每秒 $1$ 个单位长度的速度沿数轴向右运动，动点 $N$ 从点 $B$ 出发，以每秒 $2$ 个单位长度的速度沿数轴向左运动，点 $M$ ， $N$ 同时出发，当点 $N$ 到达点 $A$ 时，两动点的运动同时停止 $.$ 设运动时间为 $t$ 秒，则：
$①$ 点 $M$ 、 $N$ 表示的数分别是▲、 ▲ $($ 用含 $t$ 的代数式表示 $)$ ；
$②$ 若在运动过程中，存在 $C M = 3 C N$ ，请求出 $t$ 的值．

(3)、【方法迁移】我们发现角的很多运算方法和线段一样，如图 $2$ ， $∠ A O B = 80 °$ ， $O C$ 平分 $∠ A O B .$ 射线 $O M$ 从 $O A$ 出发，以每秒 $1 °$ 的速度绕点 $O$ 顺时针旋转，射线 $O N$ 从 $O B$ 出发，以每秒 $2 °$ 的速度绕点 $O$ 逆时针旋转 $.$ 射线 $O M$ ， $O N$ 同时出发，当 $O N$ 到达 $O A$ 时，运动同时停止 $.$ 设旋转时间为 $t$ 秒，若在运动过程中，存在某些时刻，使得 $∠ C O M$ 和 $∠ C O N$ 两个角中，其中一个角是另一个角的 $3$ 倍，请求出所有符合题意的 $t$ 的值．

查看试题解析