湖南省长沙市长沙县2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-04-01 类型:期末考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 如图,将绕点按逆时针方向旋转后得到 , 若 , 则的度数是( )
 A、 B、 C、 D、2. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、平行四边形 B、等边三角形 C、等腰梯形 D、圆3. 下列函数是二次函数的是( )A、 B、 C、 D、4. 下列说法中,正确的是( )A、同心圆的周长相等 B、面积相等的圆是等圆 C、相等的圆心角所对的弧相等 D、平分弧的弦一定经过圆心5. 已知的半径为2,点O到直线l的距离是4,则直线l与的位置关系是( )A、相离 B、相切 C、相交 D、以上情况都有可能6. 下列事件是必然事件的是( )A、车辆随机到达一个路口遇到红灯 B、早上的太阳从西方升起
A、 B、 C、 D、2. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、平行四边形 B、等边三角形 C、等腰梯形 D、圆3. 下列函数是二次函数的是( )A、 B、 C、 D、4. 下列说法中,正确的是( )A、同心圆的周长相等 B、面积相等的圆是等圆 C、相等的圆心角所对的弧相等 D、平分弧的弦一定经过圆心5. 已知的半径为2,点O到直线l的距离是4,则直线l与的位置关系是( )A、相离 B、相切 C、相交 D、以上情况都有可能6. 下列事件是必然事件的是( )A、车辆随机到达一个路口遇到红灯 B、早上的太阳从西方升起
C、人中有两人的生日在同一天 D、掷一枚质地均匀的硬币正面朝上7. 已知反比例函数的图象上有三点 , , 则、、的大小关系为( )A、 B、 C、 D、8. 若与相似,且对应边之比为: , 则与的面积比为( )A、: B、: C、: D、:9. 一个二次函数图象的顶点坐标是 , 且过另一点 , 则这个二次函数的解析式为( )A、 B、 C、 D、10. 古希腊著名的科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即“阻力阻力臂动力动力臂”小明同学用撬棍撬动一块大石头,已知阻力和阻力臂分别是和 , 则动力单位:关于动力臂单位:的函数表达式正确的是( )A、 B、 C、 D、二、填空题:本题共6小题,每小题3分,共18分。
-
11. 水稻育秧前都要提前做好发芽试验,特别是高水分种子,确保发芽率达到以上,保证成苗率,现有 , 两种新水稻种子,为了解它们的发芽情况,在推广前做了五次发芽实验,每次随机各自取相同的种子数,在相同的培育环境中分别实验,实验情况记录如下:
种子数量
发芽率
发芽率
下面有两个推断:
当实验种子数量为时,两种种子的发芽率均为 , 所以 , 两种新水稻种子发芽的概率一样;
随着实验种子数量的增加,种子发芽率在附近摆动,显示出一定的稳定性,可以估计种子发芽的概率是 . 其中合理的是 .12. 如图,为反比例函数图象上一点,垂直轴于点 , 若 , 则 . 13. 将抛物线y= (x-1)2 +3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为14. 如图,点是等边三角形的中心, , , 分别是 , , 的中点,则与是位似三角形此时,与的位似比为 .
13. 将抛物线y= (x-1)2 +3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为14. 如图,点是等边三角形的中心, , , 分别是 , , 的中点,则与是位似三角形此时,与的位似比为 .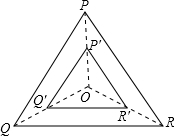 15. 如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于8,则⊙O的面积等于.
15. 如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于8,则⊙O的面积等于.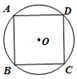 16. 如图,二次函数的图象与轴交于 , 两点,与轴交于点,且对称轴为 , 点坐标为则下面的四个结论:;;;当时,或其中正确的是 .
16. 如图,二次函数的图象与轴交于 , 两点,与轴交于点,且对称轴为 , 点坐标为则下面的四个结论:;;;当时,或其中正确的是 .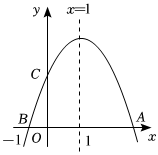
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
-
17. 如图,是经过某种变换得到的图形,点与点 , 点与点 , 点与点分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
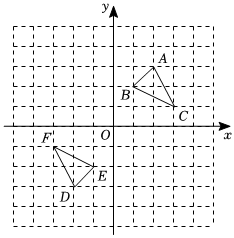 (1)、填写完整:点与点 , 点与点 , 点与点的坐标,并说说对应点的坐标有哪些特征;
(1)、填写完整:点与点 , 点与点 , 点与点的坐标,并说说对应点的坐标有哪些特征;
与 ; 与 , 与 . 对应点坐标的特征:横坐标、纵坐标均 .(2)、若点与点也是通过上述变换得到的对应点,求 , 的值.18. 长沙地铁的开通运营缓解了城市的交通压力,如图所示的是某站地铁闸口的示意图.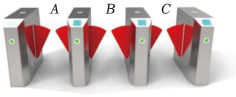 (1)、一名乘客通过此地铁闸口进站时,选择闸口的概率是 .(2)、当两名乘客通过此地铁闸口进站时,请用树状图或列表法求两名乘客选择不同的闸口通过的概率.19. 如图, , .
(1)、一名乘客通过此地铁闸口进站时,选择闸口的概率是 .(2)、当两名乘客通过此地铁闸口进站时,请用树状图或列表法求两名乘客选择不同的闸口通过的概率.19. 如图, , .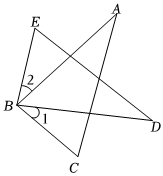
求证:(1)、∽;
(2)、 .20. 如图,一次函数的图象与反比例函数的图象交于第一象限 , 两点,与坐标轴交于、两点,连接 , 是坐标原点 .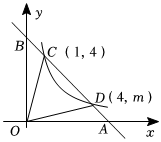 (1)、求反比例函数的表达式及的值;(2)、根据函数图象,直接写出不等式的解集为 .21. 如图,在中,弦 , 相交于点 , 连接 , 已知 .
(1)、求反比例函数的表达式及的值;(2)、根据函数图象,直接写出不等式的解集为 .21. 如图,在中,弦 , 相交于点 , 连接 , 已知 .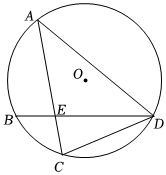 (1)、求证:;(2)、连接、 , 若 , 的半径为 , 求的长.22. 在“校园劳动节”活动中,某劳动小组借助如图所示的直角墙角墙角两边和足够长 , 用长的篱笆围成一个矩形劳动基地篱笆只围和两边 , 设 , 则 .
(1)、求证:;(2)、连接、 , 若 , 的半径为 , 求的长.22. 在“校园劳动节”活动中,某劳动小组借助如图所示的直角墙角墙角两边和足够长 , 用长的篱笆围成一个矩形劳动基地篱笆只围和两边 , 设 , 则 .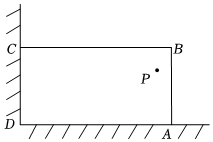 (1)、求与之间的关系式,并写出自变量的取值范围;(2)、当矩形劳动基地的面积为时,求的长;(3)、如果在点处有一棵树不考虑粗细 , 它与墙和的距离分别是和 , 如果要将这棵树围在矩形劳动基地内部含边界 , 试求矩形劳动基地面积的最大值.23. 如图,为的直径,为上一点,的平分线交于点 , 于点 .
(1)、求与之间的关系式,并写出自变量的取值范围;(2)、当矩形劳动基地的面积为时,求的长;(3)、如果在点处有一棵树不考虑粗细 , 它与墙和的距离分别是和 , 如果要将这棵树围在矩形劳动基地内部含边界 , 试求矩形劳动基地面积的最大值.23. 如图,为的直径,为上一点,的平分线交于点 , 于点 .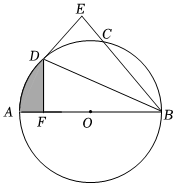 (1)、试判断与的位置关系,并说明理由;(2)、过点作于点 , 若 , , 求图中阴影部分的面积.24. 某数学学习小组在学习了相似三角形以后,他们发现对于同一个物体在灯光下,它的影子的长度与电灯到物体的距离有一定的关系,利用物体影子的长度可以计算电灯到物体的距离,利用电灯到物体的距离也可以计算物体影子的长度下面是他们的试验内容,请解答:
(1)、试判断与的位置关系,并说明理由;(2)、过点作于点 , 若 , , 求图中阴影部分的面积.24. 某数学学习小组在学习了相似三角形以后,他们发现对于同一个物体在灯光下,它的影子的长度与电灯到物体的距离有一定的关系,利用物体影子的长度可以计算电灯到物体的距离,利用电灯到物体的距离也可以计算物体影子的长度下面是他们的试验内容,请解答: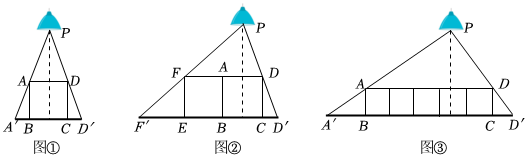 (1)、如图 , 放在水平地面上的正方形框架 , 在其正上方有一个小射灯 , 在小射灯的照射下,正方形框架在地面上的影子为、 , 若正方形框架的边长为 , , 则∽;小射灯离地面的距离为 .(2)、如图 , 不改变图中框架和小射灯的位置,将另一个同样大小的小正方形框架紧贴在原小正方形框架的左边并排摆放,即正方形求小射灯下的影长的长度.(3)、如图 , 小射灯到地面的距离为 , 一共有个边长为的小正方形框架无重叠并排如图摆放,影长与的和为用、、表示 .25. 我们把与轴有两个不同交点的函数称为“五好函数”,交点称为“五好点”,两交点间的距离称为“五好距”.(1)、判断下列函数是“五好函数”吗?如果是,请在括号里打“”,如果不是则打“”;
(1)、如图 , 放在水平地面上的正方形框架 , 在其正上方有一个小射灯 , 在小射灯的照射下,正方形框架在地面上的影子为、 , 若正方形框架的边长为 , , 则∽;小射灯离地面的距离为 .(2)、如图 , 不改变图中框架和小射灯的位置,将另一个同样大小的小正方形框架紧贴在原小正方形框架的左边并排摆放,即正方形求小射灯下的影长的长度.(3)、如图 , 小射灯到地面的距离为 , 一共有个边长为的小正方形框架无重叠并排如图摆放,影长与的和为用、、表示 .25. 我们把与轴有两个不同交点的函数称为“五好函数”,交点称为“五好点”,两交点间的距离称为“五好距”.(1)、判断下列函数是“五好函数”吗?如果是,请在括号里打“”,如果不是则打“”;
▲ ;;(2)、求出“五好函数”的“五好距”;(3)、已知“五好函数”:左侧的“五好点”位于和之间含 , 两点 , 求的取值范围;
不论取何值,不等式恒成立,在的条件下,函数为常数的最小值为 , 求的值.