新疆2024年中考数学一模考前训练卷

试卷更新日期：2024-04-01 类型：中考模拟

进入出卷网下载

一、单项选择题（本大题共9小题，每小题4分，共36分．请按答题卷中的要求作答）

1. 2024的相反数是（）

A、 $\frac{1}{2024}$ B、2024 C、 $- 2024$ D、 $- \frac{1}{2024}$

查看试题解析
2. 下列四个手机应用图标中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 港珠澳大桥是连接香港、珠海、澳门的超大型跨海通道，全长约55000米，把55000用科学记数法表示为（）

A、55×10³ B、5.5×10⁴ C、5.5×10⁵ D、0.55×10⁵

查看试题解析
4. 已知直线 $a ∥ b$ ，将一块含 $45 °$ 角的直角三角板ABC按如图方式放置，若 $∠ 1 = 24 °$ ，则 $∠ 2$ 的度数是（）

A、 $56 °$ B、 $66 °$ C、 $76 °$ D、 $86 °$

查看试题解析
5. 不等式组 ${\begin{array}{l} 2 x - 1 > 1 \\ 2 - x \geq 0 \end{array}$ 的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
6. 若一元二次方程 $a x^{2} + 2 x + 1 = 0$ 有两个不相等的实数根，则实数a的取值范围是（）

A、 $a < 1$ B、 $a \leq 1$ C、 $a \leq 1$ 且 $a \neq 0$ D、 $a < 1$ 且 $a \neq 0$

查看试题解析
7. 如图．AB、BC为⊙O的两条弦，连接OA、OC，点D为AB的延长线上一点，若∠CBD＝62°，则∠AOC的度数为（）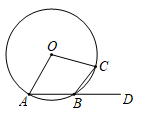

A、130° B、124° C、114° D、100°

查看试题解析
8. 如图，在 $R t △ A B C$ 中，以点 $A$ 为圆心，适当长为半径作弧，交 $A B$ 于点 $F$ ，交 $A C$ 于点 $E$ ，分别以点 $E$ ， $F$ 为圆心，大于 $\frac{1}{2} E F$ 长为半径作弧，两弧在 $∠ B A C$ 的内部交于点 $G$ ，作射线 $A G$ 交 $B C$ 于点 $D$ ．若 $A C = 3$ ， $B C = 4$ ，则 $C D$ 的长为（）

A、 $\frac{7}{8}$ B、1 C、 $\frac{3}{2}$ D、2

查看试题解析
9. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，有下列5个结论：① $a b c > 0$ ；② $b^{2} < 4 a c$ ；③ $2 c < 3 b$ ；④ $a + 2 b > m (a m + b)$ （ $m \neq 1$ ）；⑤若方程 $| a x^{2} + b x + c |$ ＝1有四个根，则这四个根的和为2，其中正确的结论有（）

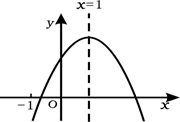A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题（本大题共6小题，每小题4分，共24分．请按答题卷中的要求作答）

10. 要使分式 $\frac{1}{x - 5}$ 有意义，则x需满足的条件是．

查看试题解析
11. 身高1.6米的小明利用影长测量学校旗杆的高度，如图，当他站在点C处时，他头顶端的影子正好与旗杆顶端的影子重合在点A处，测量得到AC=2米，CB=18米，则旗杆的高度是

查看试题解析
12. 一只不透明的袋中装有2个白球和n个黑球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸到白球的概率为 $\frac{1}{4}$ ，那么黑球的个数是.

查看试题解析
13. 如图，用一个半径为 $6 c m$ 的定滑轮拉动重物上升，拉动绳子使滑轮旋转了 $120 °$ ，则此时重物上升了 $c m$ ．（结果保留 $π$ ）

查看试题解析
14. 如图，点M在双曲线 $y = \frac{4}{x} (x > 0)$ 上，点N在双曲线 $y = \frac{1}{x} (x > 0)$ 上，且 $M N ∥ y$ 轴，则 $△ M O N$ 的面积等于．

查看试题解析
15. 如图，四边形 $A B C D$ 是矩形纸片， $A B = 2$ ，对折矩形纸片 $A B C D$ ，使 $A D$ 与 $B C$ 重合，折痕为 $E F$ ；展平后再过点B折叠矩形纸片，使点A落在 $E F$ 上的点N，折痕 $B M$ 与 $E F$ 相交于点Q；再次展平，连接 $B N$ ， $M N$ ，延长 $M N$ 交 $B C$ 于点G，有如下结论：
① $∠ A B N = 60 °$ ；② $A M = 1$ ；③ $Q N = \frac{\sqrt{3}}{3}$ ；④ $△ B M G$ 是等边三角形；⑤P为线段 $B M$ 上一动点，H是 $B N$ 的中点，则 $P N + P H$ 的最小值是 $\sqrt{3}$ ，
其中正确结论的序号是．

查看试题解析

三、解答题（本大题共8小题，共90分．解答应写出必要的文字说明、证明过程或演算步骤）

16. 计算：

(1)、 ${(- \frac{1}{2})}^{- 2} + 4 c o s 30 ° - {(3 - π)}^{0} - \sqrt{12} .$

(2)、 $(a + 3) (a - 3) - a (a - 2)$ ．

查看试题解析
17. 先化简，再求值： $(\frac{x}{x + 1} - 1) \div \frac{x^{2} - 2 x + 1}{x^{2} - 1}$ ，其中 $x = \sqrt{3} + 1$ .

查看试题解析
18. 如图，在ABCD平行四边形中，过点A作 $A E ⊥ B C$ 于点E， $A F ⊥ C D$ 于点F， $A E = A F$ ．求证：

(1)、 $△ A B E ≌ △ A D F$ ；

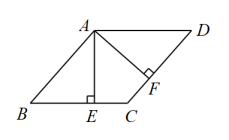(2)、四边形ABCD是菱形．

查看试题解析
19. 跳绳是某校体育活动的特色项目．体育组为了了解七年级学生1分钟跳绳次数情况，
随机抽取20名七年级学生进行1分钟跳绳测试（单位：次），数据如下：
100 110 114 114 120 122 122 131 144 148
152 155 156 165 165 165 165 174 188 190
对这组数据进行整理和分析，结果如下：
平均数
众数
中位数
145

$b$
请根据以上信息解答下列问题：

(1)、填空： $a =$ ， $b =$ ；

(2)、学校规定1分钟跳绳165次及以上为优秀，请你估计七年级240名学生中，约有多少名学生能达到优秀？

(3)、某同学1分钟跳绳152次，请推测该同学的1分钟跳绳次数是否超过年级一半的学生？说明理由．

查看试题解析
20. 如图①是一台手机支架，图②是其侧面示意图，AB、BC可分别绕点A、B转动，
测量知 $A B = 10 c m$ ， $B C = 8 c m$ ．当AB，BC转动到 $∠ B A E = 70 °$ ， $∠ A B C = 65 °$ 时，
求点C到直线AE的距离．
（精确到0.1cm，参考数据： $s i n 70 ° \approx 0.94$ ， $c o s 70 ° \approx 0.34$ ， $\sqrt{2} \approx 1.41$ ）

查看试题解析
21. 为鼓励同学们参加主题为“阅读润泽心灵，文字见证成长”的读书月活动，学校计划购进一批科技类和文学类图书作为活动奖品．已知同类图书中每本书价格相同，购买2本科技类图书和3本文学类图书需131元，购买4本科技类图书和5本文学类图书需237元．

(1)、科技类图书和文学类图书每本各多少元？

(2)、经过评选有300名同学在活动中获奖，学校对每位获奖同学奖励一本科技类或文学类图书．如果学校用于购买奖品的资金不超过8000元，那么科技类图书最多能买多少本？

查看试题解析
22. 如图， $A B$ 为 $⊙ O$ 的直径，直线与 $⊙ O$ 相切于点 $C$ ， $A D ⊥ l$ ，垂足为 $D$ ， $A D$ 交 $⊙ O$ 于点 $E$ ，连接 $C E$ ．

(1)、求证： $∠ C A D = ∠ C A B$ ；

(2)、若 $E C = 4$ ， $s i n ∠ C A D = \frac{1}{3}$ ，求 $⊙ O$ 的半径．

查看试题解析
23. 如图，已知抛物线 $y = - x^{2} + b x + c$ 与一直线相交于 $A (1 ， 0)$ ， $C (- 2 ， 3)$ 两点，与y轴交于点N ．

(1)、求抛物线的函数关系式；

(2)、求直线AC的函数关系式；

(3)、若P是抛物线上位于直线AC上方的一个动点．求 $△ A P C$ 面积的最大值．

查看试题解析

平均数	众数	中位数
145		$b$