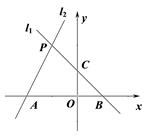人教版初中数学八年级下册 19.2.3 一次函数与方程、不等式同步分层训练提升题
试卷更新日期:2024-03-31 类型:同步测试
一、选择题
-
1. 如图,直线与x轴交点的横坐标为1,则关于x的方程的解为( ).
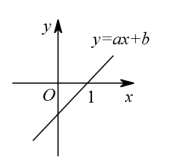 A、1 B、 C、2 D、2. 若函数和函数的图象如图所示,则关于x的不等式的解集是( )
A、1 B、 C、2 D、2. 若函数和函数的图象如图所示,则关于x的不等式的解集是( )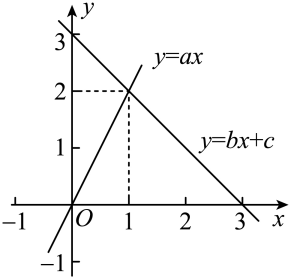 A、 B、 C、 D、3. 如图,直线与直线交于点 , 则关于x的不等式的解集为( )
A、 B、 C、 D、3. 如图,直线与直线交于点 , 则关于x的不等式的解集为( )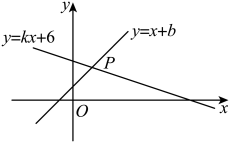 A、 B、 C、 D、4. 如图,一次函数与一次函数的图象交于点P(1,3),则关于x的不等式的解集是( )
A、 B、 C、 D、4. 如图,一次函数与一次函数的图象交于点P(1,3),则关于x的不等式的解集是( ) A、 B、 C、 D、5. 一次函数与的图象如图所示,则下列说法不正确的是( )
A、 B、 C、 D、5. 一次函数与的图象如图所示,则下列说法不正确的是( )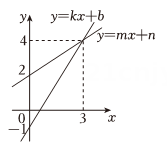 A、 B、这两个函数的图象与轴围成的三角形的面积为4. 5 C、关于的方程组的解为 D、当从0开始增加时,函数比的值先达到36. 有8条不同的直线(n=1,2,3,4,5,6,7,8),其中 , , 则这8条直线的交点个数最多是( )A、21个 B、22个 C、23个 D、24个7. 函数y=﹣kx+1(k≠0)的图象如图所示,则方程kx=1的解是( )
A、 B、这两个函数的图象与轴围成的三角形的面积为4. 5 C、关于的方程组的解为 D、当从0开始增加时,函数比的值先达到36. 有8条不同的直线(n=1,2,3,4,5,6,7,8),其中 , , 则这8条直线的交点个数最多是( )A、21个 B、22个 C、23个 D、24个7. 函数y=﹣kx+1(k≠0)的图象如图所示,则方程kx=1的解是( )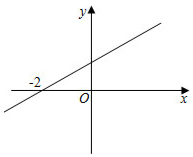 A、x=﹣2 B、x=﹣1 C、x=0 D、x=18. 如图,直线与交点的横坐标为1,若与轴的所夹儌角为 , 则方程组解为( )
A、x=﹣2 B、x=﹣1 C、x=0 D、x=18. 如图,直线与交点的横坐标为1,若与轴的所夹儌角为 , 则方程组解为( )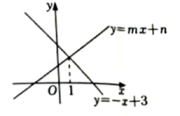 A、 B、 C、 D、无解
A、 B、 C、 D、无解二、填空题
-
9. 如图,函数与的图象相交于点 , 则关于x的不等式的解为 .
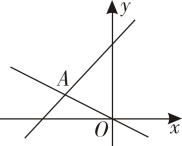 10. 用图象法解关于x,y的二元一次方程组时,小英所画图象如图所示,则该二元一次方程组的解为.
10. 用图象法解关于x,y的二元一次方程组时,小英所画图象如图所示,则该二元一次方程组的解为. 11. 如图,在中, , , 以BC所在直线为x轴,过点A作BC的垂线为y轴建立直角坐标系,D , E分别为线段AO和线段AC上一动点,且 . 当的值最小时,点E的坐标为 .
11. 如图,在中, , , 以BC所在直线为x轴,过点A作BC的垂线为y轴建立直角坐标系,D , E分别为线段AO和线段AC上一动点,且 . 当的值最小时,点E的坐标为 . 12. 已知关于x的两个一次函数 , (其中k , a均为常数).(1)、若两个一次函数的图象都经过y轴上的同一个点,则;(2)、若对于任意实数x , 都成立,则k的取值范围是.13. 如图,直线与(且,为常数)的交点坐标为 , 则关于的不等式的解集为 .
12. 已知关于x的两个一次函数 , (其中k , a均为常数).(1)、若两个一次函数的图象都经过y轴上的同一个点,则;(2)、若对于任意实数x , 都成立,则k的取值范围是.13. 如图,直线与(且,为常数)的交点坐标为 , 则关于的不等式的解集为 .
三、解答题
-
14. 已知一次函数的图象经过点 , 两点.(1)、求一次函数的表达式;(2)、求这个一次函数与坐标轴围成的三角形面积;(3)、请直接写出当时的x的取值范围。15. 如图,正比例函数的图像与一次函数的图像交于点 , 一次函数图象经过点 , 与轴的交点为 , 与轴的交点为 .
 (1)、求一次函数表达式;(2)、求点的坐标;(3)、求的面积;(4)、不解关于的方程组 , 直接写出方程组的解.
(1)、求一次函数表达式;(2)、求点的坐标;(3)、求的面积;(4)、不解关于的方程组 , 直接写出方程组的解.四、综合题