2023年吉林省中考数学真题变式题:第二十六题
试卷更新日期:2024-03-31 类型:二轮复习
一、原题重现
-
1. 如图,在平面直角坐标系中,抛物线经过点 . 点 , 在此抛物线上,其横坐标分别为 , 连接 , .
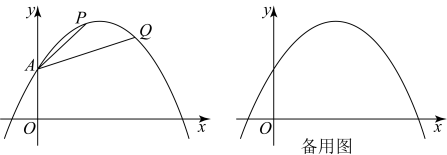 (1)、求此抛物线的解析式.(2)、当点与此抛物线的顶点重合时,求的值.(3)、当的边与轴平行时,求点与点的纵坐标的差.(4)、设此抛物线在点A与点P之间部分(包括点A和点P)的最高点与最低点的纵坐标的差为 , 在点与点之间部分(包括点和点)的最高点与最低点的纵坐标的差为 . 当时,直接写出的值.
(1)、求此抛物线的解析式.(2)、当点与此抛物线的顶点重合时,求的值.(3)、当的边与轴平行时,求点与点的纵坐标的差.(4)、设此抛物线在点A与点P之间部分(包括点A和点P)的最高点与最低点的纵坐标的差为 , 在点与点之间部分(包括点和点)的最高点与最低点的纵坐标的差为 . 当时,直接写出的值.二、变式基础练
-
2. 如图,抛物线的对称轴为直线 , 抛物线与x轴交于两点,与y轴交于点 .
 (1)、求抛物线的解析式;(2)、连接 , 在第一象限内的抛物线上,是否存在一点P , 使的面积最大?最大面积是多少?
(1)、求抛物线的解析式;(2)、连接 , 在第一象限内的抛物线上,是否存在一点P , 使的面积最大?最大面积是多少?三、变式提升练
-
3. 如图,在平面直角坐标系中,二次函数)的图象经过点A(-1,0),B(0,3),顶点的横坐标为1.
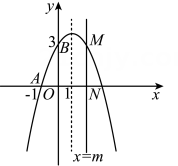 (1)、求二次函数的表达式.(2)、若直线x=m与x轴相交于点N,在第一象限内与二次函数的图象相交于点M,当m取何值时,AN+MN有最大值?求出这个最大值.(3)、若P为二次函数的图象的对称轴上一动点,将二次函数的图象向左平移1个单位后,Q为平移后二次函数的图象上一动点.在(2)的条件下求得的点M,是否能与点A,P,Q构成平行四边形?若能构成,求出点Q的坐标;若不能,请说明理由.4. 一次函数yx的图象与二次函数y=ax2﹣4ax+c(a≠0)的图象交于A , B两点(点A在点B的左侧),与这个二次函数图象的对称轴交于点C , 设二次函数图象的顶点为 D .(1)、求点C的坐标;(2)、若点D与点C关于x轴对称,且△ACD的面积等于3,求此二次函数的解析式;(3)、若CD=AC , 且△ACD的面积等于10,请直接写出满足条件的点D的坐标.5. 如图1,抛物线与x轴交于 , 两点,与y轴交于点C.
(1)、求二次函数的表达式.(2)、若直线x=m与x轴相交于点N,在第一象限内与二次函数的图象相交于点M,当m取何值时,AN+MN有最大值?求出这个最大值.(3)、若P为二次函数的图象的对称轴上一动点,将二次函数的图象向左平移1个单位后,Q为平移后二次函数的图象上一动点.在(2)的条件下求得的点M,是否能与点A,P,Q构成平行四边形?若能构成,求出点Q的坐标;若不能,请说明理由.4. 一次函数yx的图象与二次函数y=ax2﹣4ax+c(a≠0)的图象交于A , B两点(点A在点B的左侧),与这个二次函数图象的对称轴交于点C , 设二次函数图象的顶点为 D .(1)、求点C的坐标;(2)、若点D与点C关于x轴对称,且△ACD的面积等于3,求此二次函数的解析式;(3)、若CD=AC , 且△ACD的面积等于10,请直接写出满足条件的点D的坐标.5. 如图1,抛物线与x轴交于 , 两点,与y轴交于点C. (1)、求该抛物线的解析式;(2)、若点E是抛物线的对称轴与直线BC的交点,点F是抛物线的顶点,求EF的长;(3)、设点P是(1)中抛物线上的一个动点,是否存在满足的点P?如果存在,请求出P点的坐标;若不存在,请说明理由.6. 如图,在平面直角坐标系中,菱形OABC的一边OC在轴正半轴上,顶点的坐标为是边OC上的动点,过点作OB交边OA于点 , 作交边BC于点 , 连结EF,设的面积为.
(1)、求该抛物线的解析式;(2)、若点E是抛物线的对称轴与直线BC的交点,点F是抛物线的顶点,求EF的长;(3)、设点P是(1)中抛物线上的一个动点,是否存在满足的点P?如果存在,请求出P点的坐标;若不存在,请说明理由.6. 如图,在平面直角坐标系中,菱形OABC的一边OC在轴正半轴上,顶点的坐标为是边OC上的动点,过点作OB交边OA于点 , 作交边BC于点 , 连结EF,设的面积为. (1)、求关于的函数表达式.(2)、当取何值时,的值最大?请求出最大值.7. 如图,在中, , , , 点从点开始沿边向点以的速度移动,与此同时,点从点开始沿边向点以的速度移动.如果点分别从点同时出发,当点运动到点时,两点停止运动,设运动时间为ts.
(1)、求关于的函数表达式.(2)、当取何值时,的值最大?请求出最大值.7. 如图,在中, , , , 点从点开始沿边向点以的速度移动,与此同时,点从点开始沿边向点以的速度移动.如果点分别从点同时出发,当点运动到点时,两点停止运动,设运动时间为ts. (1)、 , (用t的代数式表示)(2)、经过多长时间,的面积等于?(3)、当移动时间 ▲ s时,四边形的面积最小?8. 在平面直角坐标系中,抛物线(、为常数,)与轴交于和两点,与轴交于点.(1)、请用含的代数式表示;(2)、当时,
(1)、 , (用t的代数式表示)(2)、经过多长时间,的面积等于?(3)、当移动时间 ▲ s时,四边形的面积最小?8. 在平面直角坐标系中,抛物线(、为常数,)与轴交于和两点,与轴交于点.(1)、请用含的代数式表示;(2)、当时,①若抛物线的最小值为 , 求点的坐标;
②已知点在抛物线上,若 , 直接写出的取值范围;
四、变式培优练
-
9. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 抛物线经过 , 两点,与轴的另一个交点为点 .
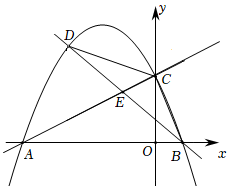 (1)、求抛物线的函数表达式.(2)、点为直线上方抛物线上一动点,连接 , , 设直线交线段于点 , 的面积为 , 的面积为 , 求的最大值.10. 如图注:与图完全相同 , 二次函数的图象与轴交于 , 两点,与轴交于点 .
(1)、求抛物线的函数表达式.(2)、点为直线上方抛物线上一动点,连接 , , 设直线交线段于点 , 的面积为 , 的面积为 , 求的最大值.10. 如图注:与图完全相同 , 二次函数的图象与轴交于 , 两点,与轴交于点 . (1)、求该二次函数的解析式;(2)、设该抛物线的顶点为 , 求的面积请在图中探索;(3)、若点 , 同时从点出发,都以每秒个单位长度的速度分别沿 , 边运动,其中一点到达端点时,另一点也随之停止运动,当 , 运动到秒时,沿所在的直线翻折,点恰好落在抛物线上点处,请直接判定此时四边形的形状,并求出点坐标请在图中探索 .11. 如图,已知抛物线与轴交于点、点位于点的左侧 , 与轴交于点 , 轴交抛物线于点 , 为抛物线的顶点.
(1)、求该二次函数的解析式;(2)、设该抛物线的顶点为 , 求的面积请在图中探索;(3)、若点 , 同时从点出发,都以每秒个单位长度的速度分别沿 , 边运动,其中一点到达端点时,另一点也随之停止运动,当 , 运动到秒时,沿所在的直线翻折,点恰好落在抛物线上点处,请直接判定此时四边形的形状,并求出点坐标请在图中探索 .11. 如图,已知抛物线与轴交于点、点位于点的左侧 , 与轴交于点 , 轴交抛物线于点 , 为抛物线的顶点.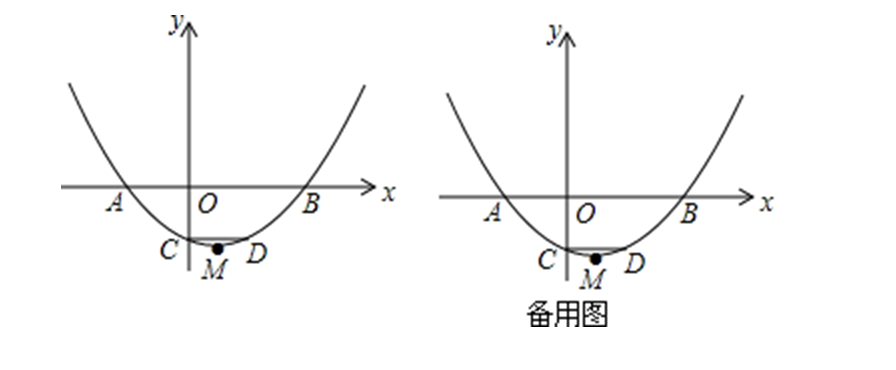 (1)、求点、、的坐标;(2)、设动点 , 求使的值最小时的值;
(1)、求点、、的坐标;(2)、设动点 , 求使的值最小时的值;
(3)、是抛物线上一点,请你探究:是否存在点 , 使以、、为顶点的三角形与相似与不重合?若存在,求出点的坐标;若不存在,说明理由.12. 如图,抛物线与轴交于点和点 , 与轴交于点 , 连接 . 点是线段下方抛物线上的一个动点(不与点重合),过点作轴的平行线交于点 , 交轴于点 .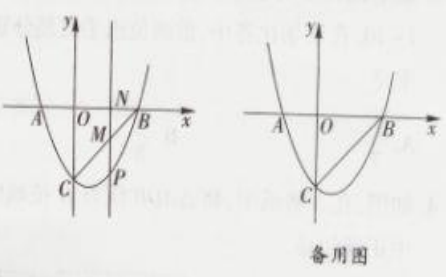 (1)、求该抛物线的解析式.(2)、过点作于点 , 且 .
(1)、求该抛物线的解析式.(2)、过点作于点 , 且 .①求点的坐标.
②连接 , 在轴上是否存在点 , 使得为直角三角形?若存在,求出点的坐标;若不存在,请说明理由.
13. 如图1,抛物线与轴交于A、B两点,与轴交于点 , 点的坐标是 , 点的坐标是 .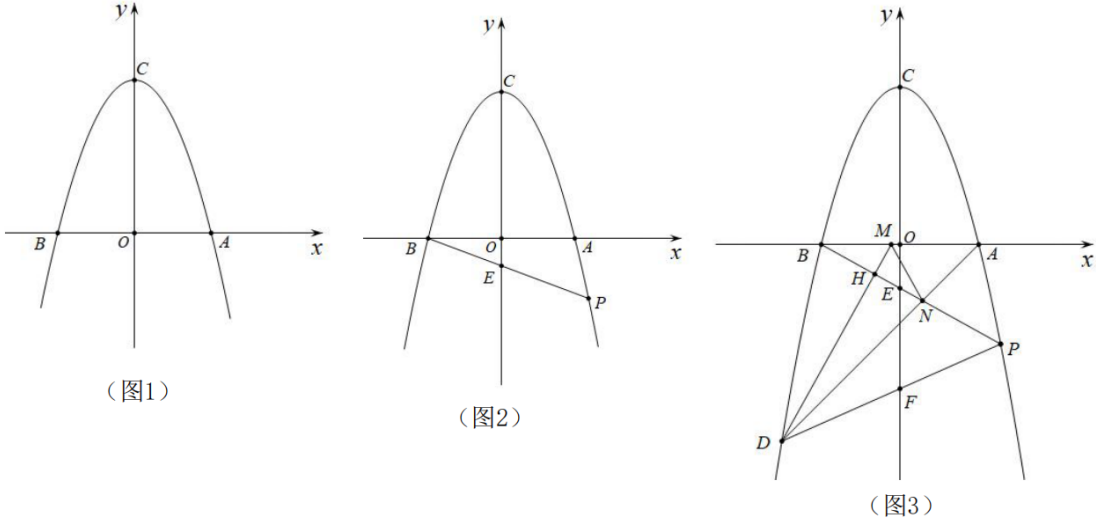 (1)、求抛物线的解析式;(2)、如图2,点是第四象限内抛物线上一点,连接PB交轴于点 , 设点的横坐标为 , 线段CE的长为 , 求与之间的函数关系式,并直接写出自变量的取值范围;(3)、如图3,点是第三象限内抛物线上一点,连接PD交轴于点 , 过点作于点 , 交轴于点 , 连接AD交BP于点 , 连接MN,若 , 时,求点的坐标.14. 在平面直角坐标系中,二次函数的图象与一次函数的图象交于点和点B,点B为二次函数图象的顶点。
(1)、求抛物线的解析式;(2)、如图2,点是第四象限内抛物线上一点,连接PB交轴于点 , 设点的横坐标为 , 线段CE的长为 , 求与之间的函数关系式,并直接写出自变量的取值范围;(3)、如图3,点是第三象限内抛物线上一点,连接PD交轴于点 , 过点作于点 , 交轴于点 , 连接AD交BP于点 , 连接MN,若 , 时,求点的坐标.14. 在平面直角坐标系中,二次函数的图象与一次函数的图象交于点和点B,点B为二次函数图象的顶点。 (1)、求二次函数和一次函数的解析式;(2)、结合图象直接写出不等式的解集;(3)、点M为二次函数图象上的一个动点,且点M的横坐标为m,将点M向右平移1个单位长度得到点N.若线段与一次函数图象有交点,直接写出点M横坐标m的取值范围。15. 在平面直角坐标系中,抛物线y=﹣x2+bx+c(b,c是常数)与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.P为x轴上方抛物线上的动点(不与点C重合),设点P的横坐标为m.
(1)、求二次函数和一次函数的解析式;(2)、结合图象直接写出不等式的解集;(3)、点M为二次函数图象上的一个动点,且点M的横坐标为m,将点M向右平移1个单位长度得到点N.若线段与一次函数图象有交点,直接写出点M横坐标m的取值范围。15. 在平面直角坐标系中,抛物线y=﹣x2+bx+c(b,c是常数)与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.P为x轴上方抛物线上的动点(不与点C重合),设点P的横坐标为m.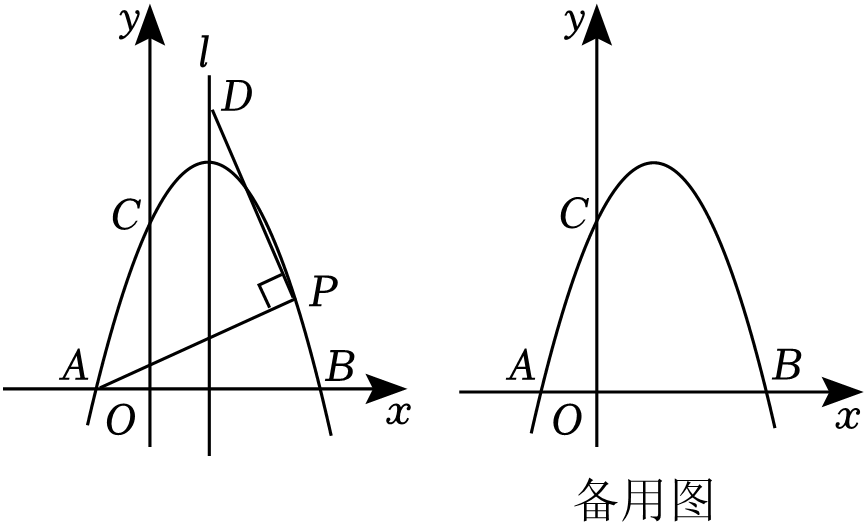 (1)、直接写出b,c的值;(2)、如图,直线l是抛物线的对称轴,当点P在直线l的右侧时,连接PA,过点P作PD⊥PA,交直线l于点D.若PA=PD,求m的值;(3)、过点P作x轴的平行线与直线BC交于点Q,线段PQ的长记为d.
(1)、直接写出b,c的值;(2)、如图,直线l是抛物线的对称轴,当点P在直线l的右侧时,连接PA,过点P作PD⊥PA,交直线l于点D.若PA=PD,求m的值;(3)、过点P作x轴的平行线与直线BC交于点Q,线段PQ的长记为d.①求d关于m的函数解析式;
②根据d的不同取值,试探索点P的个数情况.
16. 如图,直线与x轴交于点C , 与y轴交于点B , 抛物线经过B , C两点. (1)、 求抛物线的解析式;(2)、 点E是线BC上方抛物线上的一动点,当其到直线BC的距离最大时,求点E的坐标;(3)、点Q是抛物线对称轴上的动点,在抛物线上是否存在点P , 使得以P , Q , B , C为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、 求抛物线的解析式;(2)、 点E是线BC上方抛物线上的一动点,当其到直线BC的距离最大时,求点E的坐标;(3)、点Q是抛物线对称轴上的动点,在抛物线上是否存在点P , 使得以P , Q , B , C为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
-
-