2023年吉林省中考数学真题变式题:第二十五题
试卷更新日期:2024-03-31 类型:二轮复习
一、解答题
-
1. 如图,在正方形中, , 点是对角线的中点,动点 , 分别从点 , 同时出发,点以的速度沿边向终点匀速运动,点以的速度沿折线向终点匀速运动.连接并延长交边于点 , 连接并延长交折线于点 , 连接 , , , , 得到四边形 . 设点的运动时间为()(),四边形的面积为()

 (1)、的长为 , 的长为 . (用含x的代数式表示)(2)、求关于的函数解析式,并写出自变量的取值范围.(3)、当四边形是轴对称图形时,直接写出的值.
(1)、的长为 , 的长为 . (用含x的代数式表示)(2)、求关于的函数解析式,并写出自变量的取值范围.(3)、当四边形是轴对称图形时,直接写出的值.二、变式基础练
-
2. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF,求证:△ABE≌△BCF.
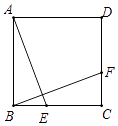 3. 如图,在正方形 ABCD中,点 E 在 BC 边的延长线上,点 F 在 CD 边的延长线上,且 CE=DF,连结 AE和BF.求证:AE=BF.
3. 如图,在正方形 ABCD中,点 E 在 BC 边的延长线上,点 F 在 CD 边的延长线上,且 CE=DF,连结 AE和BF.求证:AE=BF. 4. 在平面直角坐标系中,分别是轴、轴正半轴上的点,是线段上一点,连接 .
4. 在平面直角坐标系中,分别是轴、轴正半轴上的点,是线段上一点,连接 .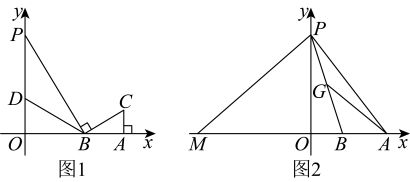 (1)、如图1,轴于点是上一点,且;
(1)、如图1,轴于点是上一点,且;①求证:;
②若 , 求证:;
(2)、如图2,是的中点,连接是轴负半轴上一点, , 当点在轴正半轴上运动时,点的坐标是否会发生变化,若不变,求点的坐标,若改变,求出其变化的范围.5. 已知:如图,E,F是正方形的对角线上的两点,且 . 求证:四边形是菱形.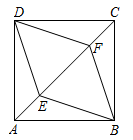 6. 如图,在平行四边形中,点、分别在、延长线上,且求证:四边形为平行四边形.
6. 如图,在平行四边形中,点、分别在、延长线上,且求证:四边形为平行四边形.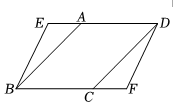
三、变式提升练
-
7. 如图,在▱ 中,点 , 分别是 , 的中点,点 , 在对角线 上,且 .
 (1)、求证:四边形 是平行四边形;(2)、连接 交 于点 ,若 , ,求 的长.8. 如图,点E是正方形内一点,将绕点A顺时针旋转至 , 点E的对应点为点F .
(1)、求证:四边形 是平行四边形;(2)、连接 交 于点 ,若 , ,求 的长.8. 如图,点E是正方形内一点,将绕点A顺时针旋转至 , 点E的对应点为点F . (1)、若 , , 求的度数.(2)、连接 , 若 , 求线段的长.9. 如图,在正方形中, , 以点为圆心,长为半径画弧,求阴影部分的面积(结果保留)
(1)、若 , , 求的度数.(2)、连接 , 若 , 求线段的长.9. 如图,在正方形中, , 以点为圆心,长为半径画弧,求阴影部分的面积(结果保留)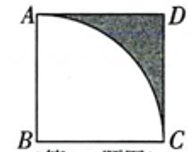 10. 如图,四边形ABCD的四个顶点分别在反比例函数与的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.
10. 如图,四边形ABCD的四个顶点分别在反比例函数与的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4. (1)、当m=4,n=20时,
(1)、当m=4,n=20时,①若点P的纵坐标为2,求直线AB的函数表达式.
②若P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)、四边形ABCD能否为正方形?若能,求此时m,n之间的数量关系;若不能,请说明理由.11. 如图,点 , 分别在正方形的边 , 上,且 , 把绕点顺时针旋转得到 .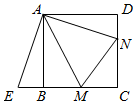 (1)、求证:≌ .(2)、若 , , 求正方形的边长.12.(1)、解方程:.(2)、如图:在正方形ABCD中,点E、F在AC上,且 , 求证:四边形BEDF是菱形.
(1)、求证:≌ .(2)、若 , , 求正方形的边长.12.(1)、解方程:.(2)、如图:在正方形ABCD中,点E、F在AC上,且 , 求证:四边形BEDF是菱形. 13. 某小区院内有一块边长为米的正方形地 , 现在物业部门计划将该地的周围进行绿化(如图中阴影部分).中间部分将修建一个长为米,宽为米的长方形景点.
13. 某小区院内有一块边长为米的正方形地 , 现在物业部门计划将该地的周围进行绿化(如图中阴影部分).中间部分将修建一个长为米,宽为米的长方形景点. (1)、用含a、b的式子表示绿化的面积;(2)、求出当 , 时的绿化面积.14. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB , D为AB边上一点,过点D作DE⊥BC , 交直线MN于E , 垂足为F , 连接CD、BE .
(1)、用含a、b的式子表示绿化的面积;(2)、求出当 , 时的绿化面积.14. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB , D为AB边上一点,过点D作DE⊥BC , 交直线MN于E , 垂足为F , 连接CD、BE .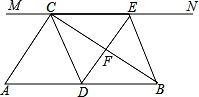 (1)、求证:CE=AD;(2)、当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
(1)、求证:CE=AD;(2)、当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.四、变式培优练
-
15. 在正方形中,对角线 , 交于点 , , 是上的两点,连接 , 分别过点 , 作的垂线 , , 垂足分别为 , .
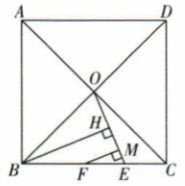 (1)、若 , 求证:;(2)、若 , 求证:;(3)、若是的中点,则线段 , , 之间存在一定的数量关系,请直接写出来.16. 在正方形ABCD中,点G是边AB上的一个动点,点F、E在边BC上, , 且、GF、DE的延长线相交于点P.
(1)、若 , 求证:;(2)、若 , 求证:;(3)、若是的中点,则线段 , , 之间存在一定的数量关系,请直接写出来.16. 在正方形ABCD中,点G是边AB上的一个动点,点F、E在边BC上, , 且、GF、DE的延长线相交于点P. (1)、如图1,当点E与点C重合时,的度数=;(2)、如图2,当点E与C不重合时,在点G的运动过程中,的度数是否发生变化,若不变,求出的度数,若变化,请说明理由(3)、在(2)的条件下,如图3,过D作于点N,连接CN.BP,取BP的中点M,连接MN,在点G的运动过程中,求的值(直接写出结果即可).17. 如图,直线与坐标轴分别交于点 , , 以为边在轴的右侧作正方形 .
(1)、如图1,当点E与点C重合时,的度数=;(2)、如图2,当点E与C不重合时,在点G的运动过程中,的度数是否发生变化,若不变,求出的度数,若变化,请说明理由(3)、在(2)的条件下,如图3,过D作于点N,连接CN.BP,取BP的中点M,连接MN,在点G的运动过程中,求的值(直接写出结果即可).17. 如图,直线与坐标轴分别交于点 , , 以为边在轴的右侧作正方形 . (1)、求点 , 的坐标;(2)、如图,点是轴上一动点,点在的右侧, , .
(1)、求点 , 的坐标;(2)、如图,点是轴上一动点,点在的右侧, , .
探究发现,点在一条定直线上,请直接写出该直线的解析式_▲_ ;
若点是线段的中点,另一动点在直线上,且 , 请求出点的坐标.18. 矩形AOBC在平面直角坐标系中的位置如图所示,点A在x轴的负半轴上,点B在y轴的正半轴上,连接AB , 将△ABC沿AB折叠得△ABE , AE交y轴于点D , 线段OD、OA的长是方程x2-7x+12=0的两个根,且OA>OD. (1)、请直接写出点A的坐标为 , 点D的坐标为;(2)、点P为直线AB上一点,连接PO、PD , 当△POD的周长最小时,求点P的坐标;(3)、点M在x轴上,点N在直线AB上,坐标平面内是否在点Q , 使以B、M、N、Q为顶点的四边形为正方形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.19. 如图1,内接于 , 为直径,点D为上一点,连接交于点G,于点F交于点E.
(1)、请直接写出点A的坐标为 , 点D的坐标为;(2)、点P为直线AB上一点,连接PO、PD , 当△POD的周长最小时,求点P的坐标;(3)、点M在x轴上,点N在直线AB上,坐标平面内是否在点Q , 使以B、M、N、Q为顶点的四边形为正方形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.19. 如图1,内接于 , 为直径,点D为上一点,连接交于点G,于点F交于点E. (1)、求证:;(2)、如图2,连接 , 若 , 求证:;(3)、在(2)的条件下,如图3,点H是上一点,连接 , , 若 , 求线段的长.
(1)、求证:;(2)、如图2,连接 , 若 , 求证:;(3)、在(2)的条件下,如图3,点H是上一点,连接 , , 若 , 求线段的长.
-