2023年吉林省中考数学真题变式题：第二十四题

试卷更新日期：2024-03-31 类型：二轮复习

进入 出卷网 下载

一、原题重现

  • 1.

    (1)、【操作发现】如图①，剪两张对边平行的纸条，随意交叉叠放在一起，使重合的部分构成一个四边形EFMN ． 转动其中一张纸条，发现四边形EFMN总是平行四边形其中判定的依据是 ．
    (2)、【探究提升】取两张短边长度相等的平行四边形纸条ABCD和EFGH（AB<BC ， FG≤BC），其中AB=EF ， ∠B=∠FEH ， 将它们按图②放置，EF落在边BC上，FG ， EH与边AD分别交于点M，N．求证：▱EFMN是菱形．
    (3)、【结论应用】保持图②中的平行四边形纸条ABCD不动，将平行四边形纸条EFGH沿BC或CB平移，且EF始终在边BC上．当MD=MG时，延长CD ， HG交于点P，得到图③．若四边形ECPH的周长为40，sin∠EFG=45（∠EFG为锐角），则四边形ECPH的面积为 ．   

    查看试题解析

二、变式基础练

  • 2. 如图，在▱ABCD中，已知AE=CF ， DM=BN ， EF与MN交于点O ， 且MN⊥EF ．

    (1)、试判断四边形ENFM的形状，并说明理由．
    (2)、若∠B=2∠MNF ， 且MN=4 ， EF=2 ， 求AB的长．

    查看试题解析

  • 3. 已知点E、F分别是平行四边形ABCD的边BC、AD的中点．

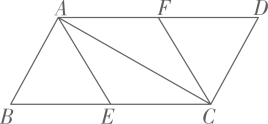    (1)、求证：四边形AECF是平行四边形；
    (2)、若BC=12 ， ∠BAC=90° ， 求平行四边形AECF的周长．

    查看试题解析

三、变式提升练

  • 4. 如图，已知在平行四边形ABCD中，AE平分∠BAD交BC于点E ， 点F在AD上，AF＝AB ， 连接BF交AE于点O ， 连接EF ．

    (1)、求证：四边形ABEF是菱形；
    (2)、若BF＝8，AB＝5，求AE的长．

    查看试题解析

  • 5. 如图，在▱ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F，连接EF．求证：四边形ABEF是菱形．

    查看试题解析

  • 6. 如图，在四边形ABCD中，E，F分别是AD，BC的中点，G，H分别是对角线BD，AC的中点，依次连接E，G，F，H，连接EF，GH．

    (1)、求证：四边形EGFH是平行四边形；
    (2)、当AB＝CD时，EF与GH有怎样的位置关系？请说明理由．

    查看试题解析

  • 7. 如图，在四边形ABCD中，AB∥DC ， AB＝AD ， 对角线AC ， BD交于点O ， AC平分∠BAD ， 过点C作CE⊥AB ， 交AB的延长线于点E ， 连接OE ．

    (1)、求证：四边形ABCD是菱形．
    (2)、若AB＝5，BD＝6，求OE的长．

    查看试题解析

  • 8. 如图，平行四边形ABCD中，AD=9cm ， CD=32cm ， ∠B=45° ， 点M ， N分别以A ， C为起点，1cm/秒的速度沿AD ， CB边运动，设点M ， N运动的时间为t秒(0≤t≤6) ．

    (1)、求BC边上高AE的长度；
    (2)、连接AN ， CM ， 当t为何值时，四边形AMCN为菱形；
    (3)、作MP⊥BC于P ， NQ⊥AD于Q ， 当t为何值时，四边形MPNQ为正方形．

    查看试题解析

  • 9. 如图，在菱形ABCD中，AC是对角线，点E是线段AC延长线上的一点，在线段CA的延长线上截取AF=CE ， 连接DF ， BF ， DE ， BE.试判断四边形FBED的形状，并说明理由．

    查看试题解析

  • 10.  如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M ， 与BD相交于点O ， 与BC相交于点N ， 连接BM、DN ．
    (1)、求证：四边形BMDN是菱形；
    (2)、若AB=4 ， AD=8 ， 求△BMD的面积．

    查看试题解析

  • 11. 如图所示，四边形ABCD为平行四边形，AE平分∠BAD交BC于点E ， 过点E作EF//AB ， 交AD于点F ， 连结BF.

    (1)、求证：BF平分∠ABC.
    (2)、若AB=6 ， 且四边形ABCD与四边形CEFD相似，求BC的长.

    查看试题解析

  • 12. 如图，在△ABC中，点D、E、F分别在BC、AB、AC边上，且DE//AC ， DF//AB ．

    (1)、如果∠BAC=90°那么四边形AEDF是形；
    (2)、如果AD是△ABC的角平分线，那么四边形AEDF是形；
    (3)、如果∠BAC=90° ， AD是△ABC的角平分线，那么四边形AEDF是    ▲    形，证明你的结论(仅需证明第3)题结论)

    查看试题解析

四、变式培优练

  • 13. 如图，在矩形ABCD中，O为对角线BD的中点，∠ABD=60°，动点E在线段OB上，动点F在线段OD上，点E，F同时从点O出发，分别向终点B，D运动，且始终保持OE=OF．点E关于AD ，AB的对称点为E1 ， E2；点F关于BC，CD的对称点为F1 ， F2 ， 在整个过程中，四边形E1E2F1F2形状的变化依次是（ ）

    A、菱形→平行四边形→矩形→平行四边形→菱形 B、菱形→正方形→平行四边形→菱形→平行四边形 C、平行四边形→矩形→平行四边形→菱形→平行四边形 D、平行四边形→菱形→正方形→平行四边形→菱形

    查看试题解析

  • 14. 如图，在四边形ABCD中，AB∥CD，AC平分∠DAB，AB=2CD，E为AB的中点，连结CE．

    (1)、求证：四边形AECD为菱形；
    (2)、若∠D=120°，DC=2，求△ABC的面积

    查看试题解析

  • 15. 如图，在Rt△ABC中，∠ACB=90° ， 过点C的直线MN//AB ， D为AB边上一点，过点D作DE⊥BC ， 交直线MN于E ， 垂足为F ， 连接CD、BE ．

    (1)、求证：CE=AD；
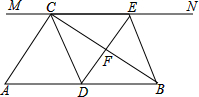    (2)、当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由；
    (3)、若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．

    查看试题解析

  • 16. 如图，在菱形ABCD中，点E在BC边上，仅用无刻度直尺完成下列画图，保留作图痕迹，不需要写作法．

     

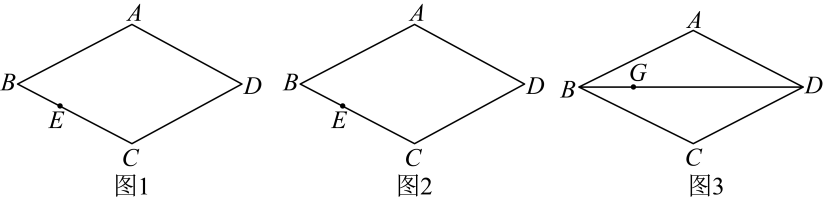    (1)、如图1，在AD上画点F，使四边形AECF是平行四边形；
    (2)、如图2，在CD上画点K，使CK=CE；
    (3)、如图3，若点G在BD上，在BD上画点H，使四边形AGCH是菱形．

    查看试题解析

  • 17. 在矩形ABCD中，AB=3 ， BC=4 ， E ， F是对角线AC上的两个动点，分别从A ， C同时出发相向而行，速度均为1cm/s ， 运动时间为t秒，当其中一个动点到达后就停止运动．

    (1)、若G ， H分别是AB ， DC中点，求证：四边形EGFH始终是平行四边形．
    (2)、在(1)条件下，当t为何值时，四边形EGFH为矩形．
    (3)、若G ， H分别是折线A−B−C ， C−D−A上的动点，与E ， F相同的速度同时出发，当t为何值时，四边形EGFH为菱形．

    查看试题解析

  • 18. 如图，在四边形ABCD中，AB∥CD ， 过点D作∠ADC的角平分线交AB于点E，连接AC交DE于点O，AD∥CE ．

    (1)、求证：四边形AECD是菱形；
    (2)、若AD=10 ， △ACD的周长为36，求菱形AECD的面积．

    查看试题解析

  • 19. 在正方形ABCD中，AB=6 ， E、F分别是BC、AB边上的动点，以DF、EF为边作平行四边形EFDG ．

    (1)、如图1，连接AE ， 交DF于点O，若AF=BE ．

    ①试说明EG与AE的关系；

    ②线段DG最小值是    ▲        ；

    (2)、如图2，若四边形EFDG为菱形，判断线段BE与AF之间的数量关系，并说明理由．

    查看试题解析

  • 20. 在四边形ABCD中，AD∥BC，AB=8cm，AD=16cm，BC=22cm，∠ABC=90°．点P从点A出发，以1cm/s的速度向点D运动，点Q从点C同时出发，以3cm/s的速度向点B运动，其中一个动点到达端点时，另一个动点也随之停止运动，设运动时间为t秒．

    (1)、当t=时，四边形ABQP成为矩形？
    (2)、当t=时，以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形？
    (3)、四边形PBQD是否能成为菱形？若能，求出t的值；若不能，请说明理由，并探究如何改变Q点的速度（匀速运动），使四边形PBQD在某一时刻为菱形，求点Q的速度．

    查看试题解析