2023年吉林省中考数学真题变式题：第二十三题

试卷更新日期：2024-03-31 类型：二轮复习

进入出卷网下载

一、原题重现

1. 甲、乙两个工程组同时挖掘沈白高铁某段隧道，两组每天挖掘长度均保持不变，合作一段时间后，乙组因维修设备而停工，甲组单独完成了剩下的任务，甲、乙两组挖掘的长度之和 $y (m)$ 与甲组挖掘时间x（天）之间的关系如图所示．

(1)、甲组比乙组多挖掘了天．

(2)、求乙组停工后y关于x的函数解析式，并写出自变量x的取值范围．

(3)、当甲组挖掘的总长度与乙组挖掘的总长度相等时，直接写出乙组己停工的天数．

查看试题解析

二、变式基础练

2. 我们知道，海拔高度每上升1千米，温度下降 $6 ℃$ ，某时刻，上海地面温度为 $20 ℃$ ，设高出地面 $x$ 千米处的温度为 $y ℃$ ．

(1)、写出 $y$ 与 $x$ 之间的函数关系式，并写出函数定义域；

(2)、有一架飞机飞过浦东上空，如果机舱内仪表显示飞机外面的温度为 $- 16 ℃$ ，求此刻飞机离地面的高度为多少千米？

查看试题解析
3. 如图，把一些相同规格的碗整齐地叠放在水平桌面上，这摞碗的高度随着碗的数量变化而变化的情况如表格所示：
碗的数量（只） 1 2 3 4 5 ······
高度（cm） 4 5.2 6.4 7.6 8.8 ······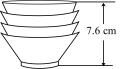

(1)、上述两个变量之间的关系中，哪个是自变量？哪个是因变量？

(2)、用h（cm）表示这摞碗的高度，用 $x$ （只）表示这摞碗的数量，请用含有 $x$ 的代数式表示h；

(3)、若这摞碗的高度为11.2cm，求这摞碗的数量.

查看试题解析
4. 学校举行大型活动，用甲、乙两架无人机进行航拍，若无人机在上升过程中匀速飞行，甲先从地面起飞，在空中停留一会儿后继续上升，此时乙从地面起飞，无人机所在高度 $h$ （米）与时间 $t$ （秒）之间的关系如图所示，根据图象回答下列问题：

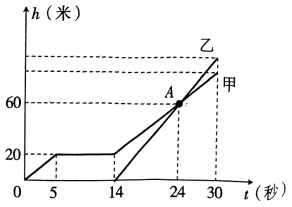(1)、甲在空中停留时的高度是米，甲出发秒后乙开始起飞，点 $A$ 表示的意义是；

(2)、甲、乙两架无人机的上升速度分别是多少米/秒？

(3)、当 $t = 30$ 时，两架无人机所在的高度相差多少米？

查看试题解析
5. 如图，A、B两地相距120千米，甲、乙两人骑车同时分别从A、B两地相向而行匀速行驶，设他们各自距A地的距离S（千米）都是骑车时间t的一次函数，并回答下列问题：

(1)、甲的速度为千米/小时，乙的速度为千米/小时；

(2)、求运动过程中 $l_{乙}$ 的函数解析式.

查看试题解析
6. 物理实验证实：在弹性限度内，某弹簧长度y（ $cm$ ）与所挂物体质量x（ $kg$ ）满足函数关系 $y = k x + 15$ ．下表是测量物体质量时，该弹簧长度与所挂物体质量的数量关系．

x

0

2

5

y

15

19

25

(1)、求y与x的函数关系式；

(2)、当弹簧长度为20 $cm$ 时，求所挂物体的质量．

查看试题解析

三、变式提升练

7. 一天下午，某网约车师傅开车从威宁到贵阳，汽车出发前油箱中有25升油，行驶一段时间后，师傅感觉有点疲倦，于是就到服务区休息了一会儿.当师傅打算继续上路向贵阳方向行驶时，发现油箱中的油不多了，于是就在该服务区的加油站加了油（加油时间忽略不计），才继续上路行驶.已知进入服务区前和驶出服务区后汽车都匀速行驶，汽车行驶时每小时的耗油量一定.油箱中剩余油量 $Q$ （升）与汽车的行驶时间 $t$ （时）之间的函数图象如图所示.

(1)、师傅开车行驶小时后去服务区休息，此时用了升油.

(2)、求进入服务区前的 $Q$ 与 $t$ 之间的函数关系式.

(3)、加完油时，刚好是下午4：40，此时距贵阳还有136千米，若汽车行驶的速度为85千米/时，师傅能在下午6：10前赶到贵阳吗？

(4)、若该师傅到达贵阳后，接到客人又马上返回威宁，请问他不加油行吗？

查看试题解析

8. 根据表中素材，探索完成以下任务：

建设“美丽乡村”，落实“乡村振兴”

问题情境

素材1

已知甲、乙两仓库分别有水泥40吨和60吨．

素材2

现在A村需要水泥48吨，B村需要水泥52吨．

素材3

从甲仓库往A，B两村运送水泥的费用分别为20元/吨和25元/吨；

从乙仓库往A，B两村运送水泥的费用分别为15元/吨和24元/吨．

问题解决

分析

设从甲仓库运往A村水泥x吨，补全以下表格．

	运量（吨）		运费（元）
	甲仓库	乙仓库	甲仓库	乙仓库
A村	x	$48 - x$	$20 x$	$15 (48 - x)$
B村	$40 - x$	① ▲	$25 (40 - x)$	② ▲

问题1

设总运费为y元，请写出y与x的函数关系式并求出最少总运费．

问题2

为了更好地支援乡村建设，甲仓库运往A村的运费每吨减少 $a (4 < a < 8)$ 元，这时甲仓库运往A村的水泥多少吨时总运费最少？最少费用为多少元？（用含a的代数式表示）

查看试题解析

9. 根据市场需求，某书城准备购进甲、乙两种青少年喜欢的读本进行销售，它们的进价和售价如下表．
读本
进价（元/本）
售价（元/本）
甲
30
45
乙
20
30
现计划用不超过1850元购进这两种读本共80本，并将这80本读本全部售完，
设购进甲种读本x本，这两种读本的总利润为y元．

(1)、求y与x的函数关系式．

(2)、该书城如何进货才能获得最大利润？最大利润是多少？

查看试题解析
10. 一名生物学家在研究两种不同的物种A和B在同一生态环境中的资源消耗时发现：50个物种A和100个物种B共消耗了200单位资源；100个物种A和50个物种B共消耗了250单位资源．

(1)、求1个物种A和1个物种B各消耗多少单位资源；

(2)、已知物种A ， B共有200个且A的数量不少于100个．设物种A有a个，物种A ， B共消耗的单位资源W ．
①求W与a的函数关系式；
②当物种A的数量为何值时，物种A、B共消耗的单位资源最少，最小值是多少？

查看试题解析
11. 甲、乙两支清雪队同时开始清理某路段积雪，一段时间后，乙队被调往别处，甲队又用了3小时完成了剩余的清雪任务，已知甲队每小时的清雪量保持不变，乙队每小时清雪50吨，甲、乙两队在此路段的清雪总量y（吨）与清雪时间x（时）之间的函数图象如图所示．

(1)、乙队调离时，甲、乙两队已完成的清雪总量为吨；

(2)、求此次任务的清雪总量m；

(3)、求乙队调离后y与x之间的函数关系式，并注明取值范围．

查看试题解析
12. 我校的饮水机接通电源就进入自动程序，开机加热时每分钟上升 $10 ° C$ ，加热到 $100 ° C$ ，停止加热，水温开始下降，此时水温（ $° C$ ）与开机后用时（min）成反比例关系.直至水温降至 $20 ° C$ 时自动开机加热，重复上述自动程序.若在水温为 $20 ° C$ 时，接通电源后，水温 $y (° C)$ 和时间x（min）的关系如图所示.

(1)、 $a =$ ， $b =$ .

(2)、直接写出图中y关于x的函数表达式.

(3)、饮水机有多少时间能使水温保持在 $50 ° C$ 及以上？

(4)、若某天上午7：00饮水机自动接通电源，开机温度正好是 $20 ° C$ ，问学生上午第一节下课时（8：40）能喝到 $50 ° C$ 以上的水吗？请说明理由.

查看试题解析
13. 通过心理专家实验研究发现：初中生在数学课上听课注意力指标随上课时间的变化而变化，指标达到或超过 36 时为认真听讲阶段，学生注意力指标y随时间x(分钟)变化的函数图象如图所示.当0≤x≤10 和10≤x≤20时，图象是不同的线段，当 20≤x≤45 时，图象是反比例函数的一部分.

(1)、求点 A 对应的指标值.

(2)、李老师在一节课上讲一道数学综合题需17分钟，他能否通过适当的安排，使讲解在学生认真听讲阶段进行? 请说明理由.

查看试题解析
14. 探索计算：弹簧挂上物体后会伸长，已知一弹簧的长度 $(c m)$ 与所挂物体的质量 $(k g)$ 之间的关系如表，
所挂物体的质量/kg
0
1
2
3
4
5
6
7
弹簧的长度/cm
12
12.5
13
13.5
14
14.5
15
15.5

(1)、在弹性限度内如果所挂物体的质量为 $x k g$ ，弹簧的长度为 $y c m$ ，根据上表写出 $y$ 与 $x$ 之间的关系式；

(2)、如果弹簧的最大长度为 $20 c m$ ，那么该弹簧最多能挂的物体质量为多少?

查看试题解析

四、变式培优练

15. 随着"5G”时代的到来，一种新型打车方式受到大众欢迎.该打车方式的计价规则如图1所示，若车辆以平均速度 $v k m / h$ 行驶了 $s k m$ ，则打车费用为 $(p s + 60 q \cdot \frac{s}{v})$ 元(不足9元按9元计价).小明某天用该打车方式出行，按上述计价规则，其打车费用 $y$ (元)与行驶里程 $x (k m)$ 的函数关系也可用图2表示.

(1)、当 $x ⩾ 6$ 时，求 $y$ 与 $x$ 的函数关系式.

(2)、若 $p = 1 ， q = 0.5$ ，求该车行驶的平均速度.

查看试题解析
16. 甲、乙两地之间有一条笔直的公路，小明从甲地出发步行前往乙地，同时小亮从乙地出发骑自行车前往甲地，小亮到达甲地没有停留，按原路原速返回，追上小明后两人一起步行到乙地．如图，线段OA表示小明与甲地的距离 $y_{1}$ （米）与行走的时间x（分钟）之间的函数关系：折线BCDA表示小亮与甲地的距离 $y_{2}$ （米）与行走的时间x（分钟）之间的函数关系，请根据图象解答下列问题：

(1)、小明步行的速度是米/分钟，小亮骑自行车的速度是米/分钟；

(2)、线段OA与BC相交于点E ，求点E坐标；

(3)、请直接写出小亮从乙地出发到追上小明的过程中，与小明相距100米时x的值．

查看试题解析
17. 为了鼓励居民节约用水，某地区决定实行两级收费制度．若每月用水量不超过14m³（含14m³），则每立方米按政府补贴优惠价m元收费；若每月用水量超过14m³ ，则超过部分每立方米按市场价n元收费．小明家3月份用水20m³ ，缴纳水费49元；4月份用水18m³ ，缴纳水费42元．

(1)、每立方米水政府补贴优惠价和市场价分别是多少？

(2)、设每月用水量为x（m³），应缴纳水费为y（元），写出y关于x的函数表达式．

(3)、小明家5月份用水26m³ ，则他家应缴纳水费多少元？

查看试题解析
18. 某商场准备购进甲乙两种服装进行销售．甲种服装每件进价160元，售价220元；乙种服装每件进价120元，售价160元．现计划购进两种服装共100件，其中甲种服装不少于60件．设购进甲种服装x件，两种服装全部售完，商场获利y元．

(1)、求y与x之间的函数关系式；

(2)、若购进100件服装的总费用不超过15000元，求最大利润为多少元？

(3)、在（2）的条件下，该服装店对甲种服装以每件优惠a（ $0 ＜ a ＜ 20$ ）元的价格进行优惠促销活动，乙种服装每件进价减少b元，售价不变，且 $a - b = 4$ ，若最大利润为4950元，求a的值．

查看试题解析
19.
甲、乙两人同时从同一地点向目的地出发，甲、乙两人相对于出发地的距离 $y (m)$ 与时间 $x (m i n)$ 之间的关系如图所示．

(1)、甲、乙两人的平均速度分别是多少？

(2)、试分别确定甲、乙两人相对于出发地的距离 $y (m)$ 与时间 $x (m i n)$ 之间的关系式？

(3)、3分钟时，甲、乙两人之间的距离是多少米？

查看试题解析

碗的数量（只）	1	2	3	4	5	······
高度（cm）	4	5.2	6.4	7.6	8.8	······

所挂物体的质量/kg	0	1	2	3	4	5	6	7
弹簧的长度/cm	12	12.5	13	13.5	14	14.5	15	15.5

读本	进价（元/本）	售价（元/本）
甲	30	45
乙	20	30