2023年吉林省中考数学真题变式题：第二十一题

试卷更新日期：2024-03-31 类型：二轮复习

进入出卷网下载

一、原题重现

1. 某校数学活动小组要测量校园内一棵古树的高度，王朵同学带领小组成员进行此项实践活动，记录如下：

填写人：王朵综合实践活动报告时间：2023年4月20日

活动任务：测量古树高度

活动过程

【步骤一】设计测量方案

小组成员讨论后，画出如图①的测量草图，确定需测的几何量．

【步骤二】准备测量工具

自制测角仪，把一根细线固定在半圆形量角器的圆心处，细线的另一端系一个小重物，制成一个简单的测角仪，利用它可以测量仰角或俯角，如图②所示准备皮尺．

【步骤三】实地测量并记录数据如图③，王朵同学站在离古树一定距离的地方，将这个仪器用手托起，拿到眼前，使视线沿着仪器的直径刚好到达古树的最高点．

如图④，利用测角仪，测量后计算得出仰角 $α$ ．

测出眼睛到地面的距离 $A B$ ．

测出所站地方到古树底部的距离 $B D$ ．

$α =$ ．

$A B = 1.54 m$ ．

$B D = 10 m$ ．

【步骤四】计算古树高度 $C D$ ．（结果精确到 $0.1 m$ ）

（参考数据： $s i n 40 ° = 0.643 ， c o s 40 ° = 0.766 ， t a n 40 ° = 0.839$ ）

请结合图①、图④和相关数据写出 $α$ 的度数并完成【步骤四】．

查看试题解析

二、变式基础练

2. 已知在Rt△ABC中，∠C=90°，∠A= $α$ ， BC=m，那么AB的长为（）

A、 $m s i n α$ B、 $m c o s α$ C、 $\frac{m}{s i n α}$ D、 $\frac{m}{c o s α}$

查看试题解析
3. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 相交于点 $O$ ， $D E ⊥ A C$ 于点 $E$ ， $∠ E D C$ ： $∠ E D A = 1$ ： $2$ ，且 $D E = 2 \sqrt{3}$ ，则 $A C$ 的长度是（）

A、 $2 \sqrt{5}$ B、 $2$ C、 $8$ D、 $\frac{5 \sqrt{3}}{3}$

查看试题解析

三、变式提升练

4. 构建几何图形解决代数问题是“数形结合”思想的体现，在计算 $t a n 15 °$ 时，如图1，在 $R t △ A C B$ 中， $∠ C = 90 ° ， ∠ A B C = 30 °$ ，延长 $C B$ 使 $B D = A B$ ，连接 $A D$ ，得 $∠ D = 15 °$ ，所以 $t a n 15 ° = \frac{A C}{C D} = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ．类比这种方法，

(1)、类比这种方法，求得 $t a n 22.5 ° =$ ；

(2)、如图2，锐角 $∠ A B C = α$ ，已知 $t a n α = m$ ，求证： $t a n \frac{α}{2} = \frac{\sqrt{m^{2} + 1} - 1}{m}$ ．

查看试题解析
5. 两千多年前，古希腊数学家欧多克索斯发现：将一条线段AB分割成长、短两条线段AP、PB，若 $\frac{P B}{A P} = \frac{A P}{A B}$ ，则把这种分割叫做黄金分割，点P叫做线段AB的黄金分割点，这个比值叫做黄金比．

图① 图② 图③

(1)、如图①，点P是线段AB的黄金分割点，设 $A B = 1$ ， $A P = x$ ，求黄金比x的值．
（精确到0.001，参考数据： $\sqrt{2} = 1.4142$ ， $\sqrt{3} = 1.7321$ ， $\sqrt{5} = 2.2361$ ， $\sqrt{6} = 2.4495$ ）

(2)、如图②，在△ABC中， $A B = A C$ ， $∠ A = 36 °$ ， BD是△ABC的角平分线．
求证：点D是线段AC的黄金分割点．

(3)、如图③，点E是正方形ABCD的BC边的中点，以点E为圆心以ED长为半径画弧，交射线BC于点F，过点F作 $F G ⊥ B C$ 交射线AD于点G．若 $A G = 2 \sqrt{5}$ ，请直接写出AB的长．

查看试题解析
6. [探究与证明]折纸，操作简单，富有数学趣味，我们可以通过折纸开展数学探究，探索数学奥秘．
[动手操作]如图①，将矩形纸片ABCD对折，使AD与BC重合，展平纸片，得到折痕EF；折叠纸片，使点B落在EF上，并使折痕经过点A，得到折痕AM，点B，E的对应点分别为B'，E'，展平纸片，连结AB'，BB'，BE'．请完成：

(1)、观察图①中∠1，∠2和∠3，试猜想这三个角的大小关系；

(2)、证明(1)中的猜想；

(3)、[类比操作]如图②，N为矩形纸片ABCD的边AD上的一点，连接BN，在AB上取一点P，折叠纸片，使B，P两点重合，展平纸片，得到折痕EF ；折叠纸片，使点B，P分别落在EF，BN上，得到折痕l，点B，P的对应点分别为B'，P'，展平纸片，连接BB'，P'B'．请完成：
求证：BB'是∠NBC的一条三等分线．

查看试题解析
7. 如图

(1)、如图1，在矩形ABCD中，点E，F分别在边DC，BC上，AE⊥DF，垂足为点G．求证：△ADE∽△DCF．

(2)、【问题解决】如图2，在正方形ABCD中，点E，F分别在边DC，BC上，AE＝DF，延长BC到点H，使CH＝DE，连接DH．求证：∠ADF＝∠H．

(3)、【类比迁移】如图3，在菱形ABCD中，点E，F分别在边DC，BC上，AE＝DF＝11，DE＝8，∠AED＝60°，求CF的长．

查看试题解析

(1)、【教材呈现】下图是华师版数学教材八年级下册第117页的部分内容

例5如图19.2.13，已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F ，求证：四边形AFCE是菱形.

分析要证四边形AFCE是菱形，由已知条件可知 $E F ⊥ A C$ ，所以只需证明四边形AFCE是平行四边形，又知EF垂直平分AC ，所以只需证 $O E = O F$ .

图19.2.13

请根据教材分析，结合图①，写出完整的证明过程

(2)、证明【结论应用】如图②，直线EF分别交矩形ABCD的边AD、BC于点E、F ，将矩形ABCD沿EF翻折，使点C与点A重合，点D落到点

D^{'}

处.若

A F = 5

，

D^{'} E = 3

，则矩形ABCD的面积为.

查看试题解析

9. 【教材呈现】下面是华师版教材九年级上册52页的部分内容：

我们可以发现，当两条直线与一组平行线相交时，所截得的线段存在一定的比例关系： $\frac{A D}{D B} = \frac{F E}{E C}$ ．这就是如下的基本事实：

两条直线被一组平行线所截，所得的对应线段成比例．（简称“平行线分线段成比例”）

(1)、【问题原型】如图①，在矩形ABCD中，点E为边AB的中点，过E作EF∥AD交边DC于点F，点P、Q分别在矩形的边AD、BC上，连结PQ交EF于点M．求证：PM＝QM．

(2)、【结论应用】如图②，在【问题原型】的基础上，点R在边BC上（不与点Q重合），连结PR交EF于点N．
若MN＝4，则线段QR的长为；

(3)、当点Q与点B重合，点R与点C重合时，如图③，若BC＝10，且△PMN周长的最小值为12，则边AB的长为．

查看试题解析

10. [教材呈现]如图是华师版教材九年级上册52页的部分内容：
我们可以发现，当两条直线与一组平行线相交时，所截得的线段存在一定的比例关系： $\frac{A D}{D B} = \frac{F E}{E C}$ ．这就是如下的基本事实：
两条直线被一组平行线所截，所得的对应线段成比例。
（简称“平行线分线段成比例" ）

(1)、[问题原型]如图①，在矩形ABCD中，点E为边AB的中点，过E作EF∥AD交，边DC于点F，点P、Q分别在矩形的边AD、BC上，连接PQ交EF于点M．求证： PM= QM；

(2)、[结论应用]如图②，在[问题原型]的基础上，点R在边BC上（不与点Q重合），
连接PR交EF于点N．
①若MN=4，则线段QR的长为
②当点Q与点B重合，点R与点C重合时，如图③，若BC=10，且△PMN周长的最小值为12，则边AB的长为

查看试题解析

四、变式培优练

11. 定义：长宽比为 $\sqrt{n} ： 1$ （n为正整数）的矩形称为 $\sqrt{n}$ 矩形．下面，我们通过折叠的方式折出一个 $\sqrt{2}$ 矩形，如图①所示．
操作1：将正方形 $A B C D$ 沿过点 $B$ 的直线折叠，使折叠后的点 $C$ 落在对角线 $B D$ 上的点 $G$ 处，折痕为 $B H$ ．
操作2：将 $A D$ 沿过点 $G$ 的直线折叠，使点 $A$ ，点 $D$ 分别落在边 $A B$ ， $C D$ 上，折痕为 $E F$ ．
则四边形 $B C E F$ 为 $\sqrt{2}$ 矩形．
证明：设正方形 $A B C D$ 的边长为1，则 $B D = \sqrt{1^{2} + 1^{2}} = \sqrt{2}$ ．
由折叠性质可知 $B G = B C = 1$ ， $∠ A F E = ∠ B F E = 90 °$ ，则四边形 $B C E F$ 为矩形，
∴ $∠ A = ∠ B F E$ ， ∴ $E F ∥ A D$ ．
∴ $\frac{B G}{B D} = \frac{B F}{A B}$ ，即 $\frac{1}{\sqrt{2}} = \frac{B F}{1}$ ， ∴ $B F = \frac{1}{\sqrt{2}}$ ， ∴ $B C ： B F = 1 ： \frac{1}{\sqrt{2}} = \sqrt{2} ： 1$ ，
∴四边形 $B C E F$ 为 $\sqrt{2}$ 矩形．
阅读以上内容，回答下列问题：

(1)、在图①中，所有与 $C H$ 相等的线段是、， $t a n ∠ H B C$ 的值是；

(2)、已知四边形 $B C E F$ 为 $\sqrt{2}$ 矩形，模仿上述操作，得到四边形 $B C M N$ ，如图②，求证：四边形 $B C M N$ 为 $\sqrt{3}$ 矩形；

(3)、将图②中的 $\sqrt{3}$ 矩形 $B C M N$ 沿用（2）中的方式操作3次后，得到一个“ $\sqrt{n}$ 矩形”，则 $n$ 的值是．

查看试题解析
12.

(1)、问题提出如图①，在矩形ABCD中，∠ABC的平分线交AD于点E，连接CE，若AD＝9，∠DCE＝15°，求△BCE外接圆的半径长．

(2)、问题解决某社区准备设计一个矩形花园，如图②是花园的示意图，图中EF，EG，FG，FC是花园内四条小路，这四条小路将花园分成五个三角形区域，分别用来种植不同种类的花．根据设计要求，∠EGF＝∠BCF，∠EFC＝90°，DF：DC＝1：2，AE＝8米．该矩形花园面积是否存在最大值？若存在，请求出其最大面积；若不存在，请说明理由．

查看试题解析
13. 已知四边形ABCD中，E ， F分别是AB ， AD边上的点，DE与CF交于点G ，令＝k ．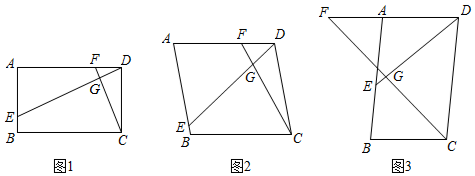

(1)、特例解析：如图1，若四边形ABCD是矩形，且DE⊥CF ，求证： $\frac{D E}{C F}$ ＝k；

(2)、类比探究：如图2，若四边形ABCD是平行四边形，当∠B与∠EGC满足什么关系时， $\frac{D E}{C F}$ ＝k仍然成立？并证明你的结论；

(3)、拓展延伸：如图3，在（2）的条件下， $k = \frac{5}{7} ， A D = 5 ， t a n ∠ D C F = \frac{4}{3}$ ， ∠AED＝45°，求DE的长．

查看试题解析
14. 如图，在平面直角坐标系中， $A (0 ， 2)$ ， $B (3 ， 0)$ ，过点 $B$ 作直线 $l ∥ y$ 轴，点 $P$ 是直线 $l$ 上的动点，以 $A P$ 为边在 $A P$ 右上侧作等腰直角 $△ A P Q$ ，使 $∠ A P Q = 90 °$ ．

(1)、如图1当点 $P$ 落在点 $B$ 时，则点 $Q$ 的坐标是；

(2)、学生甲认为点 $Q$ 的坐标一定跟点 $P$ 有关，于是进行了如下探究：
如图2，小聪同学画草图时，让点 $P$ 落在 $P_{1}$ 、 $P_{2}$ 、 $P_{3}$ 不同的特殊位置时（ $P_{1}$ 在 $x$ 轴上、 $P_{2} A$ 与 $x$ 轴平行、当 $Q$ 落在 $x$ 轴上时对应点 $P_{3}$ ），画出了几个点对应的 $Q_{1}$ 、 $Q_{2}$ 、 $Q_{3}$ 三个不同的位置，发现 $Q_{1}$ 、 $Q_{2}$ 、 $Q_{3}$ 在同一条直线上，请你根据学生甲的猜测及题目条件，求出点 $Q$ 所在直线的解析式；

(3)、在（2）中，虽然求出了点 $Q$ 所在直线的解析式，但是小明同学认为几个特殊点确定解析式是一种猜测，当点 $P$ 在 $l$ 上运动时，所有的 $Q$ 点都在一条直线上吗？就解设了点 $Q$ 的坐标为 $(x ， y)$ ，希望用一般推理的方式求出 $x$ 和 $y$ 满足的关系式，请你帮助小明给出解答．

查看试题解析
15.

(1)、【观察与猜想】
如图1，点 $O$ 是矩形 $A B C D$ 内一点，过点 $O$ 的直线 $E F ⊥ M N$ ，分别交矩形的边为点 $E ， F ， M ， N$ ．若 $A D = 10 ， C D = 7 ， E F = 8$ ，则 $M N =$ ；

(2)、【类比探究】
如图2，在平行四边形 $A B C D$ 中，点 $E ， M$ 分别在边 $A B ， B C$ 上，连接 $D M$ 与 $C E$ 交于点 $O ， ∠ D O E = ∠ B$ ．求证： $C E \cdot A B = D M \cdot B C$ ；

(3)、【拓展延伸】
如图3，在四边形 $A B C D$ 中， $B C = 17 \frac{1}{5} ， A B = 4 ， ∠ B = ∠ A D C = 120 ° ， \frac{C D}{A D} = \frac{4}{5}$ ， $M$ 在边 $B C$ 上，连接 $A C$ 与 $D M$ 交于点 $O$ ，当 $∠ A O D = ∠ B$ 时，求 $\frac{A C}{D M}$ 的值．

查看试题解析
16. 综合与实践：在综合与实践课上，老师组织同学们以“矩形纸片的折叠”为主题开展数学活动，现有矩形纸片 $A B C D$ ， $A B = 12$ ， $B C = 8$ ．

(1)、操作发现
操作一：如图1，将矩形 $A B C D$ 纸片沿对角线 $A C$ 折叠，使点B落在点 $B^{'}$ 处，将纸片展平再次折叠，使点A与点C重合，折痕为 $E F$ ，然后展平得到图2，则以点A ， F ， C ， E为顶点的四边形是什么特殊四边形？并说明理由；

(2)、实践探究
操作二：如图3，在矩形纸片 $A B C D$ 中，点G为 $A B$ 的中点，将纸片沿 $C G$ 折叠，使点B落在点 $B^{'}$ 处，连接 $A B^{'}$ ．
①判断 $A B^{'}$ 与折痕 $C G$ 的位置关系，并说明理由；
②求 $A B^{'}$ 的长．

(3)、拓展应用
将矩形纸片 $A B C D$ 裁剪为 $A B = 8$ ， $B C = 6$ ，在图3的情形下，若G为 $A B$ 上任意一点，其他条件不变，当点A与点 $B^{'}$ 距离最小时，直接写出BG的长．

查看试题解析
17. [推理能力]如图，在□ABCD中，AB=2cm，AC=5cm ，S▱ABCD =8 cm²，点 E 从点 B 出发，以1cm/s的速度在 AB 的延长线上向右运动，同时点 F 从点 D 出发，以同样的速度在 CD的延长线上向左运动，运动时间为t(s).

(1)、在运动过程中，四边形 AECF 的形状是 .

(2)、当t=时，四边形 AECF 是矩形.

(3)、当 t 的值为多少时，四边形 AECF 是菱形?

查看试题解析
18. [探究与证明]折纸，操作简单，富有数学趣味，我们可以通过折纸开展数学探究，探索数学奥秘.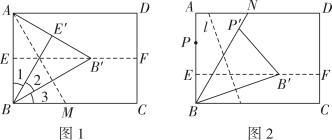
[动手操作]如图1，将矩形纸片ABCD对折，使AD与BC重合，展平纸片，得到折痕EF；折叠纸片，使点B落在EF.上，并使折痕经过点A，得到折痕AM.点B，E的对应点分别为B'，E'，展平纸片，连结AB'，BB'，BE'.请完成：

(1)、观察图1中∠1，∠2和∠3，试猜想这三个角的大小关系.

(2)、证明（1）中的猜想.

(3)、[类比操作]如图2，N为矩形纸片ABCD的边AD上的一点，连结BN，在AB上取一点P，折叠纸片，使B，P两点重合，展平纸片，得到折痕EF；折叠纸片，使点B，P分别落在EF，BN上，得到折痕l，点B，P的对应点分别为B'，P'，展平纸片，连结BB'，P'B'.请完成：
证明BB'是∠NBC的一条三等分线.

查看试题解析