2023年吉林省中考数学真题变式题：第二十题

试卷更新日期：2024-03-31 类型：二轮复习

进入出卷网下载

一、原题重现

1. 笑笑同学通过学习数学和物理知识，知道了电磁波的波长 $λ$ （单位：m）会随着电磁波的频率f（单位： $M H z$ ）的变化而变化．已知波长 $λ$ 与频率f是反比例函数关系，下面是它们的部分对应值：

频率f（ $M H z$ ）

10

15

50

波长 $λ$ （m）

30

20

6

(1)、求波长 $λ$ 关于频率f的函数解析式．

(2)、当 $f = 75 M H z$ 时，求此电磁波的波长 $λ$ ．

查看试题解析

二、变式基础练

2. 已知蓄电池的电压为定值，使用蓄电池时，电流I(A)与电阻 R(Ω)是反比例函数关系，它的图象如图所示.如果以此蓄电池为电源的用电器的限制电流为不能超过6 A，那么用电器的可变电阻R 应控制在（）

A、R≥2Ω B、0Ω<R≤2Ω C、R≥1Ω D、0Ω<R≤1Ω

查看试题解析
3. 菱形的面积为12cm² ，两条对角线分别为x(cm)和y(cm)，则y关于x的函数表达式为，当其中一条对角线x=6cm时，另一条对角线y=cm．

查看试题解析

三、变式提升练

4. 若以30升/分钟的速度向一个空水池内注水，40分钟可以注满水池，设注水的速度为 $m$ 升/分钟，注满水池需要 $t$ 分钟．

(1)、写出 $t$ 与 $m$ 之间的函数关系式；

(2)、若小明的爸爸用24分钟就将这个空水池注满水，求注水的速度．

查看试题解析
5. 某校组织活动，一小组需在室外搭建临时木屋，板对地面的压强p（Pa）是木板面积S（ $m^{2}$ ）的反比例函数，其图象如图所示，当木板的压强为500Pa时，求木板的面积．

查看试题解析
6. 在面积为定值的一组矩形中，当矩形的一条边长为7.5 cm时，它的邻边长为8 cm.

(1)、设矩形相邻的两条边长分别为x cm，y cm，求y关于x的函数解析式.这个函数是反比例函数吗?

(2)、若其中一个矩形的一条边长为5 cm，求这个矩形与之相邻的另一条边长.

查看试题解析
7. 某校科技小组进行野外考察时，为了安全、迅速通过一片十几米宽的烂泥湿地，他们沿着前进路线用若干块木板铺了一条临时通道.木板对地面的压强 p(Pa)是木板面积S(m²)的反比例函数.

(1)、求出此函数的解析式，并写出自变量取值范围；

(2)、当木板面积为0.2 m²时，压强是；

(3)、如果要求压强不超过6 000 Pa，木板的面积至少要多大?

查看试题解析
8. 为了预防疾病，某单位对办公室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y(mg)与时间x(min)成正比例，药物燃烧后，y与x成反比例(如图所示)，现测得药物8 min燃毕，此时室内空气中每立方米的含药量为6 mg，请根据题中所提供的信息，解答下列问题：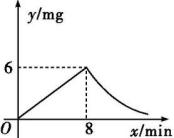

(1)、药物燃烧时，求y关于x的函数解析式，自变量x的取值范围；药物燃烧后y关于x的函数解析式.

(2)、研究表明，当空气中每立方米的含药量低于1.6 mg时员工方可进办公室，那么从消毒开始，至少经过几分钟后，员工才能回到办公室.

(3)、研究表明，当空气中每立方米的含药量不低于3 mg且持续时间不低于10 min时，才能有效杀灭空气中的病菌，那么此次消毒是否有效?为什么?

查看试题解析
9. 试验数据显示，一般成人喝半斤低度白酒后，1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(小时)的关系可近似地用二次函数y=-200x²+400x刻画，1.5小时后(包括1.5小时)y与x可近似地用反比例函数y= $\frac{k}{x}$ (k>0)刻画(如图
所示).

(1)、根据上述数学模型计算：
①喝酒多长时间后血液中的酒精含量达到最大值?最大值为多少?
②求k的值.

(2)、车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”，不能驾车上路.参照上述数学模型，假设某驾驶员晚上20：00在家喝完半斤低度白酒，第二天早上7：00能否驾车去上班?请说明理由.

查看试题解析
10. 某汽车销售公司推出购车分期付款的促销活动，支付首付款后，余额要在30个月内结清，不计算利息.王先生在活动期间购买了价格为12万元的汽车，交了首付款后平均每月付款y万元，x个月结清.y与x的函数关系如图所示，根据图象回答下列问题：

(1)、确定y与x之间的函数表达式，并求出首付款的数目.

(2)、若王先生用20个月结清，平均每月应付多少万元?

(3)、如果王先生打算每月付款不超过4 000元，那么他至少要多少个月才能结清余额?

查看试题解析
11. 方方驾驶小汽车匀速地从A地行驶到B地，行驶里程为480km，设小汽车的行驶时间为t(h)，行驶速度为v(km/h)，且全程速度限定为不超过120km/h.

(1)、求v关于t的函数表达式.

(2)、方方上午8点驾驶小汽车从A地出发，
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地，求小汽车行驶速度v的取值范围.
②方方能否在当天11点30分前到达B地?请说明理由.

查看试题解析
12. 如图，根据小孔成像的科学原理，当像距 $($ 小孔到像的距离 $)$ 和物高 $($ 蜡烛火焰高度 $)$ 不变时，火焰的像高 $y ($ 单位： $c m)$ 是物距 $($ 小孔到蜡烛的距离 $) x ($ 单位： $c m)$ 的反比例函数，当 $x = 6$ 时， $y = 2$ ．

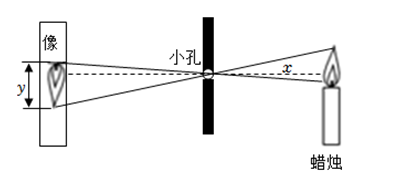(1)、求 $y$ 关于 $x$ 的函数解析式．

(2)、若火焰的像高为 $3 c m$ ，求小孔到蜡烛的距离．

查看试题解析
13. 密闭容器内有一定质量的气体，当容器的体积V（单位：m³）变化时，气体的密度ρ（单位：kg/m³）随之变化．已知密度ρ与体积V是反比例函数关系，它的图象如图所示．

(1)、求密度ρ关于体积V的函数解析式．

(2)、当V＝8m³时，求该气体的密度ρ．

查看试题解析

四、变式培优练

14. 如图，函数 $y = \frac{k}{x} (x > 0)$ 的图象过点 $A (n ， 2)$ 和 $B (\frac{8}{5} ， 2 n - 3)$ 两点．

(1)、求n和k的值；

(2)、将直线 $O A$ 沿x轴向左移动得直线 $D E$ ，交x 轴于点D ，交y 轴于点E ，交 $y = \frac{k}{x} (x > 0)$ 于点C ，若 $S_{△ A C O} = 6$ ，求直线 $D E$ 解析式；

(3)、在（2）的条件下，第二象限内是否存在点F ，使得 $△ D E F$ 是以 $D E$ 为腰的等腰直角三角形，若存在，请直接写出点F的坐标；若不存在，请说明理由．

查看试题解析
15. 通过实验研究发现：初中生在数学课上听课注意力指标随上课时间的变化而变化，上课开始时，学生兴趣激增，中间一段时间，学生的兴趣保持平稳状态，随后开始分散学生注意力指标y随时间x(分钟)变化的函数图象如图所示，当0≤x<10和10≤x<20时，图象是线段；当20≤x≤45时，图象是反比例函数图象的一部分．

(1)、求点A对应的指标值

(2)、王老师在一节数学课上讲解一道数学综合题需要17分钟，他能否经过适当的安排，使学生在听这道综合题讲解时，注意力指标都不低于36？请说明理由．

查看试题解析

频率f（ $M H z$ ）	10	15	50
波长 $λ$ （m）	30	20	6