2023年吉林省中考数学真题变式题：第十九题

试卷更新日期：2024-03-31 类型：二轮复习

进入出卷网下载

一、原题重现

1. 图①、图②、图③均是 $5 \times 5$ 的正方形网格，每个小正方形的顶点称为格点，线段 $A B$ 的端点均在格点上．在图①、图②、图③中以 $A B$ 为边各画一个等腰三角形，使其依次为锐角三角形、直角三角形、钝角三角形，且所画三角形的顶点均在格点上．

查看试题解析

二、变式基础练

2. 作图题：如图，在5×5的正方形网格中，每个小正方形的边长均为1，A ， B两点都在格点上，连结AB ，请完成下列作图．请按要求画出格点三角形．
⑴在图1中找一个格点C ，使得 $△ A B C$ 是等腰三角形（作一个即可）；
⑵在图中2找一个格点D ，使得 $△ A B D$ 是直角三角形且其三边都不与网格线重合．（作一个即可）．

查看试题解析
3. 如图是由边长为1的小正方形构成的网格，每个小正方形的顶点叫做格点，点A，B均在格点上，请用无刻度的直尺在给定的网格中按要求画图.

(1)、求AB的长；

(2)、在图①中画以AB为边的正方形ABCD，并求正方形ABCD的面积；

(3)、在图②中画以AB为边的平行四边形ABEF，使平行四边形ABEF的面积与正方形ABCD的面积相等.

查看试题解析
4. 正方形网格中的每个小正方形的边长都是1，每个小正方形顶点叫做格点，以格点为顶点画图．

(1)、在图①中，画一个面积为5的正方形 $A B C D$ ；

(2)、在图②中，画一个三角形 $A_{1} B_{1} C_{1}$ ，使它的三边长分别为 $A_{1} B_{1} = 3$ ， $A_{1} C_{1} = \sqrt{10}$ ， $B_{1} C_{1} = \sqrt{13}$ ．

查看试题解析
5. 如图，在边长为1的小正方形组成的 $9 \times 12$ 的网格中，给出了以格点(网格线的交点)为端点的线段 $A B$ .

⑴以线段 $A B$ 为一边，作正方形 $A B C D$ ，点 $C 、 D$ 都在格点上；

⑵以线段AB为一边，作平行四边形ABEF，点 $E 、 F$ 都在格点上，且 $∠ A E B = 4 5^{°}$ ，平行四边形 $A B E F$ 的面积为28；

⑶连接DF，请直接写出线段DF的长度.

查看试题解析
6. 如图，△ABC中，AB＝AC，∠A＝36°.请利用尺规作图法在AC上求作一D，使得BD把△ABC分成两个等腰三角形.（保留作图痕迹，不写作法）

查看试题解析

三、变式提升练

7. 如图，在由边长为1的小正方形构成的网格中，每个小正方形的顶点叫做格点， $△ A B C$ 的三个顶点均在格点上，点 $E$ 为AB中点，请按要求完成作图：

(1)、作线段EF，使得 $E F = A B$ ，且 $E F ⊥ A B$ ，点 $F$ 在格点上；

(2)、作线段EG，使得EG平分线段BC，点 $G$ 在格点上；

(3)、连接线段FG，直接写出线段FG的长．

查看试题解析
8. 如图在平面直角坐标系中，已知 $△ A B O$ 的顶点坐标分别是 $A (3，3)$ ， $B (- 2，2)$ ， $O (0，0)$ ．

(1)、画出 $△ A O B$ 关于 $y$ 轴对称的 $△ C O D$ ，其中点 $A$ 的对应点是点 $C$ ，点 $B$ 的对应点是点 $D$ ，并请直接写出点 $C$ 的坐标为，点 $D$ 的坐标为；

(2)、请直接写出 $△ C O D$ 的面积是；

(3)、已知点 $E$ 到两坐标轴距离相等，若 $S_{△ A O B} = 3 S_{△ B O E}$ ，则请直接写出点 $E$ 的坐标为．

查看试题解析
9. 如图，已知 $△ A B C$ 的三个顶点的坐标分别是 $A (- 4 ， 1)$ ， $B (- 3 ， 3)$ ， $C (- 1 ， 2)$ ．

(1)、画出与 $△ A B C$ 关于 $y$ 轴对称的 $△ A_{1} B_{1} C_{1}$ ，并直接写出 $A_{1} ， B_{1} ， C_{1}$ 的坐标；

(2)、在 $x$ 轴上有一点 $D$ ，使得 $△ A D C ≌ △ A B C$ ，请直接写出点 $D$ 的坐标．

查看试题解析
10. 如图， $△ A O B$ 的顶点都在边长为1的正方形组成的网格格点上， $A (- 1 ， 3) ， B (- 2 ， 2)$ ．

(1)、将 $△ A O B$ 绕点O顺时针旋转 $90 °$ 得到 $△ A_{1} O B_{1}$ ，做出旋转后的 $△ A_{1} O B_{1}$ ；

(2)、在旋转过程中，点B经过的路径为弧 $\overset{⌢}{B B_{1}}$ ，求弧 $B B_{1}$ 的长．

查看试题解析
11. 某校数学兴趣小组活动，准备将一张Rt△ABC纸片进行作图操作，以此来解决相关问题.

(1)、如图1，需将Rt△ABC纸片裁剪成面积相等的两个三角形.请你用尺规画出裁剪线，保留作图痕迹.

(2)、如图2，在Rt△ABC纸片中，∠C=90°，∠B=30°，AB=40，需将这张纸片裁剪成一个长方形，使长方形的面积是Rt△ABC面积的一半.
①画出裁剪的长方形(画出一种情况即可)；
②求裁剪所得到的长方形的周长.

查看试题解析

四、变式培优练

12. 如图所示，在 $7 \times 6$ 的方格纸中，每个小正方形的边长均为1，线段 $A B$ 的端点 $A$ 、 $B$ 均在小正方形的顶点上．

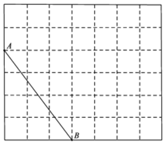(1)、在图中画出以 $A B$ 为斜边的直角三角形 $A B C$ ，点 $C$ 在小正方形顶点上，且 $\tan ∠ C B A = 2$ ；

(2)、在图中画出等腰三角形 $A B D$ ，点 $D$ 在小正方形的顶点上，且 $△ A B D$ 的面积为 $\frac{7}{2}$ ；

(3)、连接 $C D$ ，请直接写出 $\frac{B D}{C D}$ 的值．

查看试题解析
13. 如图1，在 $6 \times 8$ 的网格纸中，每个小正方形的边长都为1，动点P、Q分别从点D、A同时出发向右移动，点P的运动速度为每秒2个单位，点Q的运动速度为每秒1个单位，当点P运动到点C时，两个点都停止运动.

(1)、请在 $6 \times 8$ 的网格纸图2中画出运动时间t为2秒时的线段PQ并求其长度；

(2)、在动点P、Q运动的过程中，△PQB能否成为PQ=BQ的等腰三角形？若能，请求出相应的运动时间t；若不能，请说明理由；

(3)、在（1）中的图2中，点E如图所示，是否在PQ上存在一点M，使DM+EM的值最小，如存在，求出DM+EM最小值；如不存在，说明理由.

查看试题解析
14. 如图

问题提出

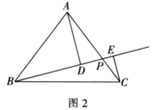
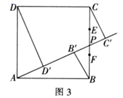
(1)、如图1，已知三角形 $A B C$ ，请在 $B C$ 边上确定一点 $D$ ，使得 $A D$ 的值最小.

(2)、如图2，在等腰 $△ A B C$ 中， $A B = A C$ ，点 $P$ 是 $A C$ 边上一动点，分别过点 $A$ ，点 $C$ 作线段 $B P$ 所在直线的垂线，垂足为点 $D ， E$ ，若 $A B = 5 ， B C = 6$ ，求线段 $B P$ 的取值范围，并求 $A D + C E$ 的最大值.

(3)、如图3，正方形 $A B C D$ 是一块蔬菜种植基地，边长为3千米，四个顶点处都建有一个蔬菜采购点，根据运输需要，经过顶点 $A$ 处和 $B C$ 边的两个三等分点 $E 、 F$ 之间的某点 $P$ 建设一条向外运输的快速通道，其余三个采购点都修建垂直于快速通道的蔬菜输送轨道，分别为 $B B^{'}$ 、 $C C^{'}$ 、 $D D^{'}$ .若你是此次项目设计的负责人，要使三条运输轨道的距离之和 $(B B^{'} + C C^{'} + D D^{'})$ 最小，你能不能按照要求进行规划，请通过计算说明.

查看试题解析