2023年吉林省中考数学真题变式题:第十七题
试卷更新日期:2024-03-31 类型:二轮复习
一、原题重现
-
1. 如图,点C在线段上,在和中, .
求证: .

二、变式基础练
-
2. 一名工作人员不慎将一块三角形模具打碎成了如图所示的四块,他需要去商店再配一块与原来大小和形状完全相同的模具.现只能拿能两块去配,其中可以配出符合要求的模具的是( )
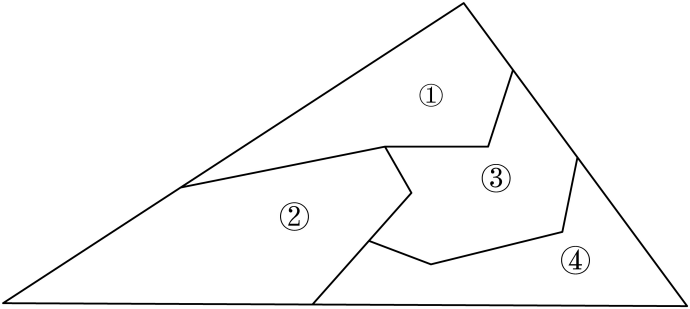 A、①③ B、②④ C、①④ D、②③3. 线段、相交于点 , , , 求证: .
A、①③ B、②④ C、①④ D、②③3. 线段、相交于点 , , , 求证: . 4. 如图,在▱ABCD中,点E在AB的延长线上,点F在CD的延长线上,且满足BE=DF.连结EF,分别与BC,AD相交于点G,H.求证:EG=FH.
4. 如图,在▱ABCD中,点E在AB的延长线上,点F在CD的延长线上,且满足BE=DF.连结EF,分别与BC,AD相交于点G,H.求证:EG=FH.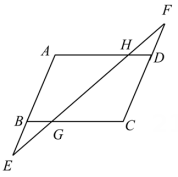 5. 如图,在△ABC中,点D在边BC上,CD=AB,DE∥AB,∠DCE=∠A.求证:DE=BC.
5. 如图,在△ABC中,点D在边BC上,CD=AB,DE∥AB,∠DCE=∠A.求证:DE=BC.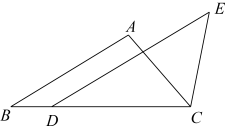 6. 如图,已知和 , , , , 与交于点 , 点在上.求证:;
6. 如图,已知和 , , , , 与交于点 , 点在上.求证:; 7. 如图,中,是边上的中线, , 为直线上的点,连接 , , 且 .
7. 如图,中,是边上的中线, , 为直线上的点,连接 , , 且 .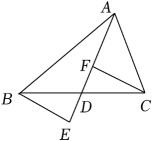 (1)、求证:;(2)、若 , , 试求的长.
(1)、求证:;(2)、若 , , 试求的长.三、变式提升练
-
8. 根据如图所示的尺规作图痕迹,下列结论不一定成立的是( )
 A、 B、 C、 D、9. 如图,的面积为平分于点P,连结 , 则的面积为( )
A、 B、 C、 D、9. 如图,的面积为平分于点P,连结 , 则的面积为( ) A、 B、 C、 D、10. 如图,在等边△ABC中,点D为AC的中点,点F在BC延长线上,点E在AB的延长线上,∠EDF=120°,若BF=9,BE=2,则AC= .
A、 B、 C、 D、10. 如图,在等边△ABC中,点D为AC的中点,点F在BC延长线上,点E在AB的延长线上,∠EDF=120°,若BF=9,BE=2,则AC= . 11. 如图,在四边形ABCD中,对角线AC , BD相交于点O , AB=AC , E是BD上一点,且∠ABD=∠ACD , ∠EAD=∠BAC.
11. 如图,在四边形ABCD中,对角线AC , BD相交于点O , AB=AC , E是BD上一点,且∠ABD=∠ACD , ∠EAD=∠BAC. (1)、 试说明:AE=AD;(2)、 若BD=8,DC=5,求ED的长.12. 如图,中, , 分别以点B,C为圆心,以大于的长为半径画弧交于M,N两点,作直线MN交BC于点O,连接AO并延长,交DC的延长线于点E,连接AC,BE.
(1)、 试说明:AE=AD;(2)、 若BD=8,DC=5,求ED的长.12. 如图,中, , 分别以点B,C为圆心,以大于的长为半径画弧交于M,N两点,作直线MN交BC于点O,连接AO并延长,交DC的延长线于点E,连接AC,BE. (1)、求证::(2)、在中能否添加一个条件,使四边形ABEC为菱形?若能,请添加后予以证明;若不能,请什么理由.13. 如图,已知:在△ABC中,AC=BC=8,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)、求证::(2)、在中能否添加一个条件,使四边形ABEC为菱形?若能,请添加后予以证明;若不能,请什么理由.13. 如图,已知:在△ABC中,AC=BC=8,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.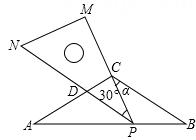 (1)、当PN∥BC时,判断△ACP的形状,并说明理由;(2)、点P在滑动时,当AP长为多少时,△ADP与△BPC全等,并说明理由;(3)、点P在滑动时,△PCD的形状可以是等腰三角形吗?若可以,
(1)、当PN∥BC时,判断△ACP的形状,并说明理由;(2)、点P在滑动时,当AP长为多少时,△ADP与△BPC全等,并说明理由;(3)、点P在滑动时,△PCD的形状可以是等腰三角形吗?若可以,请直接写出夹角α的大小; 若不可以,请说明理由.
四、变式培优练
-
14. 如图,在中, , 点D为中点, , 绕点D旋转,分别与边 , 交于E,F两点,下列结论:①;②;③;④始终为等腰直角三角形,其中正确的是( )
 A、①②④ B、①②③ C、③④ D、①②③④15. 在中, , , 点为上一点,点为上一点,线段 , 交于点 .
A、①②④ B、①②③ C、③④ D、①②③④15. 在中, , , 点为上一点,点为上一点,线段 , 交于点 . (1)、若为的角平分线.
(1)、若为的角平分线.①如图,已知 , 求证:;
②如图 , 已知 , 求证:;
(2)、如图,若为的中线,且 , 试探究 , , 三条线段的数量关系是.16.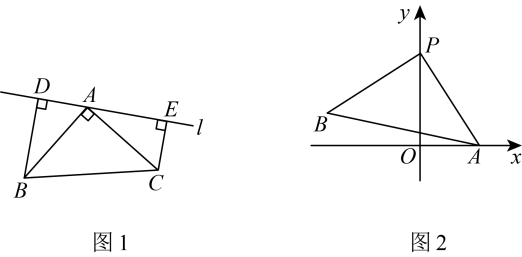 (1)、如图1,中, , , 直线经过点 , 分别过点 , 作直线的垂线,垂足分别为 , , 求证: .(2)、在(1)的条件下,猜想:线段 , , 之间的数量关系,并证明你的结论;(3)、如图2,在平面直角坐标系中, , 点是轴正半轴上的一个动点,以为直角边作等腰直角 , 点在第二象限内,且 , 在点的运动过程中,的值是否会发生变化?若不变,求出这个值;若变化,请说明理由.17. 如图(1),在平面直角坐标系中,直线交坐标轴于A、B两点,过点作交于D , 交y轴于点E . 且 .
(1)、如图1,中, , , 直线经过点 , 分别过点 , 作直线的垂线,垂足分别为 , , 求证: .(2)、在(1)的条件下,猜想:线段 , , 之间的数量关系,并证明你的结论;(3)、如图2,在平面直角坐标系中, , 点是轴正半轴上的一个动点,以为直角边作等腰直角 , 点在第二象限内,且 , 在点的运动过程中,的值是否会发生变化?若不变,求出这个值;若变化,请说明理由.17. 如图(1),在平面直角坐标系中,直线交坐标轴于A、B两点,过点作交于D , 交y轴于点E . 且 .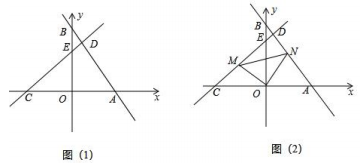 (1)、求B点坐标为;线段的长为;(2)、确定直线解析式,求出点D坐标;(3)、如图2,点M是线段上一动点(不与点C、E重合),交于点N , 连接 .
(1)、求B点坐标为;线段的长为;(2)、确定直线解析式,求出点D坐标;(3)、如图2,点M是线段上一动点(不与点C、E重合),交于点N , 连接 .①点M移动过程中,线段与数量关系是否不变,直接写出结论;
②当面积最小时,求点M的坐标和面积.
-