2023年吉林省中考数学真题变式题：第十三题

试卷更新日期：2024-03-31 类型：二轮复习

进入出卷网下载

一、原题重现

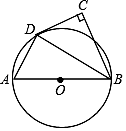
1. 如图①，A，B表示某游乐场摩天轮上的两个轿厢．图②是其示意图，点O是圆心，半径r为 $15 m$ ，点A，B是圆上的两点，圆心角 $∠ A O B = 120 °$ ，则 $\overset{⌢}{A B}$ 的长为 $m$ ．（结果保留 $π$ ）

查看试题解析

二、变式基础练

2. 若扇形的半径为3，圆心角为60°，则此扇形的弧长是（）

A、π B、 2π C、 3π D、4π

查看试题解析
3. 在半径为 $6 cm$ 的圆中，60°的圆心角所对弧的弧长是（）

A、 $πcm$ B、 $2 πcm$ C、 $3 πcm$ D、 $6 πcm$

查看试题解析
4. 若扇形的圆心角为 $4 0^{°}$ ，半径为18，则它的弧长为。

查看试题解析
5. 已知圆弧所在圆的半径为3，所对的圆心角为30°，这条弧的长为．

查看试题解析
6. 已知圆的半径为2cm，90°圆心角所对的弧长为cm.

查看试题解析
7. 如图， $A B$ 为 $⊙ O$ 的直径， $C$ 是 $⊙ O$ 上的一点，连接 $O C ， B C$ ，若 $∠ B C O = 35 ° ， A O = 2$ ，求 $\overset{⌢}{B C}$ 的长．（结果保留 $π$ ）

查看试题解析
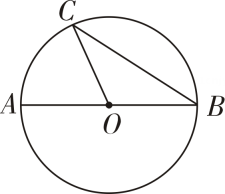8. 如图，在Rt△ABC中，∠ABC=90°，∠C=30°，D是边BC上的一点，以AD为直径的⊙O交边AC于点E，若AD=6，求 $\overset{⌢}{E B}$ 的长（结果保留π）．

查看试题解析

三、变式提升练

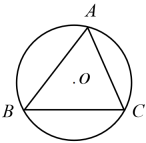
9. 如图，△ABC内接于⊙O ， ∠B=65°，∠C=70°若BC= $2 \sqrt{2}$ ，则 $\hat{BC}$ 的长为（）

A、π B、 $\sqrt{2}$ π C、2π D、2 $\sqrt{2}$ π

查看试题解析
10. 如图，在平面直角坐标系 $x O y$ 中，点A坐标为 $(- 8 ， 0)$ ，点B坐标为 $(0 ， 6)$ ， $⊙ O$ 的半径为4（O为坐标原点），点C是 $⊙ O$ 上一动点，过点B作直线 $A C$ 的垂线 $B P$ ， P为垂足，点C在 $⊙ O$ 上运动一周，则点P运动的路径长等于（）

A、 $\frac{5 π}{3}$ B、 $\frac{8 π}{3}$ C、 $\frac{10 π}{3}$ D、 $\frac{20 π}{3}$

查看试题解析
11. 如图，正六边形 $A B C D E F$ 内接于 $⊙ O$ ， $⊙ O$ 的半径为6，则这个正六边形的边心距 $O M$ 和弧 $B C$ 的长分别为（）

A、 $\frac{3}{2}$ ， $π$ B、 $\frac{3 \sqrt{3}}{2}$ ， $π$ C、 $\frac{3 \sqrt{3}}{2}$ ， $\frac{2 π}{3}$ D、 $3 \sqrt{3}$ ， $2 π$

查看试题解析
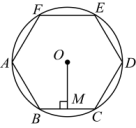12. 如图所示，王虎使一长为4 cm，宽为3 cm的长方形木板，在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A₁→A₂ ，其中第二次翻滚被桌面上一小木块挡住，使木板与桌面成30°角，则点A翻滚到A₂位置时共走过的路径长为（）

A、10 cm B、4π cm C、 $\frac{7}{2}$ π cm D、 $\frac{5}{2}$ cm

查看试题解析
13. 已知扇形面积为 $12 π$ ，半径为 $6$ ，则扇形的弧长为．

查看试题解析
14. 如图，已知 $\overset{⏜}{A B}$ 与 $\overset{⏜}{C D}$ 是公路弯道的外、内边线，它们有共同的圆心 $O$ ，所对的圆心角都是 $72 °$ 、 $A$ 、 $C$ 、 $O$ 在同一直线上，公路宽 $A C = 20$ 米，则弯道外侧边线比内侧边线多米 $($ 结果保留 $π)$ ．

查看试题解析
15. 在2022年北京冬奥会开幕式和闭幕式中，一片“雪花”的故事展现了“世界大同，天下一家”的主题，让世界观众感受了中国人的浪漫．如图，作出“雪花”图案（正六边形 $A B C D E F$ ）的外接圆，已知正六边形 $A B C D E F$ 的边长是4，则 $\overset{⌢}{B C}$ 长为．

查看试题解析
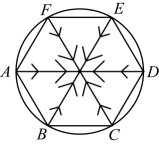16. 如图，一条公路 $($ 公路的宽度忽略不计 $)$ 的转弯处是一段圆弧 $\overset{⏜}{A B}$ ，点 $O$ 是这段弧所在圆的圆心，半径 $O A = 90 m$ ，圆心角 $∠ A O B = 80 °$ ，则这段弯路 $\overset{⏜}{A B}$ 的长度为 $m .$

查看试题解析

四、变式培优练

17. 如图，AB为⊙O的直径，点C在⊙O外，∠ABC的平分线与⊙O交于点D，∠C=90°．

(1)、CD与⊙O有怎样的位置关系？请说明理由；

(2)、若∠CDB=60°，AB=6，求 $\overset{⌢}{A D}$ 的长．

查看试题解析
18. 如图，AB是⊙O的直径，直线CD与⊙O相切于点C，且与AB的延长线交于点E．点C是弧BF的中点．

(1)、求证：AD⊥CD；

(2)、若∠CAD=30°．⊙O的半径为3，一只蚂蚁从点B出发，沿着BE--EC--弧CB爬回至点B，求蚂蚁爬过的路程(π≈3.14， $\sqrt{3}$ ≈1.73，结果保留一位小数．)

查看试题解析