2023年吉林省中考数学真题变式题:第十二题
试卷更新日期:2024-03-31 类型:二轮复习
一、原题重现
-
1. 《九章算术》中记载了一道数学问题,其译文为:有人合伙买羊,每人出5钱,还缺45钱;每人出7钱,还缺3钱.问合伙人数是多少?为解决此问题,设合伙人数为x人,可列方程为 .
二、变式基础练
-
2. 《九章算术》中记录了这样一个问题:“今有人持金十二斤出关,关税之,十分而取一.今关税取金二斤,偿钱五千,问金一斤值钱几何?”这道题的意思是:某人携带12斤金子出关,按照规定,他应交纳十分之一的税金.现在关卡收取税金2斤金子,退还5000钱,则一斤金子相当于( )A、4000钱 B、5250钱 C、6000钱 D、6250钱3. 我国古代数学著作《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽,问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完,问:城中有多少户人家?在这个问题中,城中人家的户数为( )A、25 B、75 C、81 D、904. 《九章算术》中记载了-道数学问题,其译文为:有人合伙买羊,每人出5钱,还缺45钱;每人出7钱,还缺3钱,问合伙人数是多少?为解决此问题,设合伙人数为x人,所方程正确的是( )A、5x-45=7x-3 B、5x-45=7x+3 C、5x+45=7x+3 D、5x+45=7x-35. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买一只羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设羊价为x钱,所列方程是.6. 《九章算术》中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?译文是:今有人合伙购物,每人出8钱会多3钱;每人出7钱又会差4钱,问人数、物价各是多少?设合伙人数为x人,列出的方程为 . (无需化简)7. 我国古代的《洛书》中记载了最早的三阶幻方——九宫图.在如图所示的幻方中,每行、每列、每条对角线上的三个数之和都相等,则m的值为 .
-1 2 3 m 8. 我国古代著作《九章算术》中记载了这样一个问题:“今有共买豕,人出一百,盈一百;人出九十,适足.”其大意是:“今有人合伙买猪,每人出100钱,则会多出100钱;每人出90钱,恰好合适.”若设共有x人,可求得x的值为 .三、变式提升练
-
9. 孙权曾致巨象,太祖欲知其斤重,访之群下,咸莫能出其理,冲曰:“置象大船之上,而刻其水痕所至,称物以载之,则校可知矣.”——《三国志》
按照曹冲称象的方法:先将象牵到大船上,并在船的侧面标记水位再将象牵出,然后往船上抬入20块等重的条形石,并在船上留3个搬运工,这时水位恰好到达标记位置,如果再抬入1块同样的条形石,船上只留1个搬运工,水位也恰好到达标记的位置,已知搬运工体重为130kg , 求大象的体重?设每块条形石的质量为x kg , 依题意列方程得( )
 A、20x+3×130=20x+x+130 B、20x﹣3×130=20x+x﹣130 C、20x+3×130=20x+x﹣2x130 D、20x﹣3×130=20x+x﹣2×13010. 程大位直指算法统宗:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁.意思是:有个和尚分个馒头,如果大和尚人分个,小和尚人分个,正好分完.试问大、小和尚各多少人?设大和尚有人,依题意列方程得( )A、 B、 C、 D、11. 《九章算术》中有如下问题:“以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.问绳长、井深各几何?”其题意是:用绳子测量水井深度,如果将绳子折成三等份,那么每等份绳长比水井深度多四尺;如果将绳子折成四等份,那么每等份绳长比水井深度多一尺.问绳长和井深各多少尺?设绳长为x尺,则根据题意,可列方程为( )A、 B、 C、 D、12. 明代数学家程大位的《算法统宗》中有这样一个问题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.”其大意为:有一群人分银子,如果每人分七两,则剩余四两,如果每人分九两,则还差半斤(注:明代时1斤16两,故有“半斤八两”这个成语),设有x人分银子,根据题意列方程: .13. “九宫格”源于我国古代的“洛書”,是世界上最早的“幻方”.在如图的“九宫格”中,把这个整数填入方格里,使其任意一行,任意一列及两条对角线上的三个数之和都相等,则的值为 .14. 我国古代《易经》一书中记载,远古时期人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位妇人在从右到左依次排列的绳子上打结,满五进一 , 用来记录采集到的野果的个数.她一共采集到了43个野果,则在第2根绳子上的打结数是个.
A、20x+3×130=20x+x+130 B、20x﹣3×130=20x+x﹣130 C、20x+3×130=20x+x﹣2x130 D、20x﹣3×130=20x+x﹣2×13010. 程大位直指算法统宗:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁.意思是:有个和尚分个馒头,如果大和尚人分个,小和尚人分个,正好分完.试问大、小和尚各多少人?设大和尚有人,依题意列方程得( )A、 B、 C、 D、11. 《九章算术》中有如下问题:“以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.问绳长、井深各几何?”其题意是:用绳子测量水井深度,如果将绳子折成三等份,那么每等份绳长比水井深度多四尺;如果将绳子折成四等份,那么每等份绳长比水井深度多一尺.问绳长和井深各多少尺?设绳长为x尺,则根据题意,可列方程为( )A、 B、 C、 D、12. 明代数学家程大位的《算法统宗》中有这样一个问题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.”其大意为:有一群人分银子,如果每人分七两,则剩余四两,如果每人分九两,则还差半斤(注:明代时1斤16两,故有“半斤八两”这个成语),设有x人分银子,根据题意列方程: .13. “九宫格”源于我国古代的“洛書”,是世界上最早的“幻方”.在如图的“九宫格”中,把这个整数填入方格里,使其任意一行,任意一列及两条对角线上的三个数之和都相等,则的值为 .14. 我国古代《易经》一书中记载,远古时期人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位妇人在从右到左依次排列的绳子上打结,满五进一 , 用来记录采集到的野果的个数.她一共采集到了43个野果,则在第2根绳子上的打结数是个.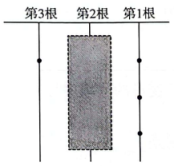 15. 一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁.——程大位《直接算法统宗》意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?16. (古代问题)某人工作一年的报酬是年终给他一件衣服和10枚银币,但他干满7个月就决定不再继续干了,结账时,给了他一件衣服和2枚银币,这件衣服值多少枚银币?17. 《直指算法统宗》中有这样一道题,原文如下:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁?”大意为:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人?请解答上述问题.
15. 一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁.——程大位《直接算法统宗》意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?16. (古代问题)某人工作一年的报酬是年终给他一件衣服和10枚银币,但他干满7个月就决定不再继续干了,结账时,给了他一件衣服和2枚银币,这件衣服值多少枚银币?17. 《直指算法统宗》中有这样一道题,原文如下:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁?”大意为:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人?请解答上述问题.四、变式培优练
-
18. 扬州雕版印刷技艺历史悠久,元代数学家朱世杰的《算学启蒙》一书曾刻于扬州,该书是中国较早的数学著作之一,书中记载一道问题:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天追上慢马?答:快马天追上慢马.19. 古代有这样一个数学问题:韩信点一队士兵人数,三人一组余两人,五人一组余三人,七人一组余四人.问这队士兵至少多少人?我国古代学者早就研究过这个问题.例如明朝数学家程大位在他著的《算法统宗》中就用四句口诀暗示了此题的解法:三人同行七十稀,五树梅花甘一枝,七子团圆正半,除百零五便得知.这四句口诀暗示的意思是:当除数分别是3,5,7时,用70乘以用3除的余数(例如:韩信点兵问题中用70乘以2),用21乘以用5除的余数,用15乘以用7除的余数,然后把三个乘积相加.加得的结果如果比105大就除以105,所得的余数就是满足题目要求的最小正整数解.按这四句口诀暗示的方法计算韩信点的这队士兵的人数为 .20. 阅读下列材料,并完成相应的任务.
我国明朝数学家程大位所著的《算法统宗》中介绍了一种计算乘法的方法,称为“铺地锦”如图1所示,计算31×47,首先把乘数31和47分别写在方格的上面和右面,然后以31的每位数字分别乘以47的每位数字,将结果计入对应的格子中(如图1,12写在3下面的方格里,十位1写在斜线的上面,个位2写在斜线的下面),再把同一斜线上的数相加,结果写在斜线末端,最后把得数依次写下来时1457,即31×47=1457.如图2,计算46×71,将乘数46写在方格上边,乘数71写在方格右边,然后用乘数46的每位数字乘以乘数71的每位数字,将结果计入相应的方格中,最后沿斜线方向相加得3266.
 (1)、如图3,用“铺地锦”计算两个数相乘,则 , .(2)、如图4,用“铺地锦”计算两个数相乘,求a的值.
(1)、如图3,用“铺地锦”计算两个数相乘,则 , .(2)、如图4,用“铺地锦”计算两个数相乘,求a的值.
-