备考2024年中考数学核心素养专题二十三 函数的综合问题
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
1. 数形结合是数学解题中常用的思想方法,使用数形结合的方法,很多问题可迎刃而解,且解法简洁.如图,直线y=3x和直线y=ax+b交于点(1,3),根据图象分析,方程3x=ax+b的解为( )
 A、x=1 B、x=-1 C、x=3 D、x=-32. 如图,直线与在第二象限交于点 , 交轴,轴分别于、两点, , 则方程组的解为( )
A、x=1 B、x=-1 C、x=3 D、x=-32. 如图,直线与在第二象限交于点 , 交轴,轴分别于、两点, , 则方程组的解为( ) A、 B、 C、 D、3. 如图,直线交轴于点 , 直线交轴于点 , 这两条直线相交于点 , 则不等式组的解集为( )
A、 B、 C、 D、3. 如图,直线交轴于点 , 直线交轴于点 , 这两条直线相交于点 , 则不等式组的解集为( ) A、 B、 C、 D、4. 如图,矩形的顶点在轴上,反比例函数的图象经过边的中点和点 , 若 , 则的值为( )
A、 B、 C、 D、4. 如图,矩形的顶点在轴上,反比例函数的图象经过边的中点和点 , 若 , 则的值为( ) A、5 B、6 C、7 D、85. 如图,的直角顶点在坐标原点上,点在反比例函数的图象上,点在反比例函数的图象上,则的值是( )
A、5 B、6 C、7 D、85. 如图,的直角顶点在坐标原点上,点在反比例函数的图象上,点在反比例函数的图象上,则的值是( )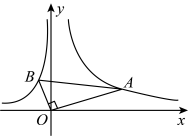 A、 B、 C、 D、6. 如图所示的是三个反比例函数y= , y= , y=在x轴上方的图象,由此观察得到k1 , k2 , k3的大小关系是( )
A、 B、 C、 D、6. 如图所示的是三个反比例函数y= , y= , y=在x轴上方的图象,由此观察得到k1 , k2 , k3的大小关系是( ) A、k1>k2>k3 B、k3>k2>k1 C、k2>k3>k1 D、k3>k1>k27. 已知抛物线y=ax2+bx+c(a , b , c是常数,a≠0,c>1)经过点(2,0),其对称轴是直线x= , 有下列结论:①abc>0;
A、k1>k2>k3 B、k3>k2>k1 C、k2>k3>k1 D、k3>k1>k27. 已知抛物线y=ax2+bx+c(a , b , c是常数,a≠0,c>1)经过点(2,0),其对称轴是直线x= , 有下列结论:①abc>0;②关于x的方程ax2+bx+c=a有两个不等的实数根;
③a<﹣ .
其中,正确结论的个数是( )
A、0 B、1 C、2 D、38. 已知二次函数为非零常数, , 当时,随的增大而增大,则下列结论正确的是( )若时,则随的增大而减小;若图象经过点 , 则;若 , 是函数图象上的两点,则;若图象上两点 , 对一切正数总有 , 则 .
A、 B、 C、 D、9. 如图,直线与抛物线交于A , B两点,且点A的横坐标是-1,点B的横坐标是4,有以下结论:①若点A在轴上,则抛物线与轴的另一个交点坐标为(3,0);②当时,一次函数与二次函数的函数值都随的增大而增大;③的长度可以等于5,其中正确的结论有( ) A、0个 B、1个 C、2个 D、3个10. 二次函数的顶点坐标为 , 其部分图象如图所示,下列结论:①;②③若点 , 点是函数图象上的两点,则;④关于x的方程无实数根;其中正确结论有( )
A、0个 B、1个 C、2个 D、3个10. 二次函数的顶点坐标为 , 其部分图象如图所示,下列结论:①;②③若点 , 点是函数图象上的两点,则;④关于x的方程无实数根;其中正确结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在平面直角坐标系内,一次函数与为常数的图象如图所示,则关于的不等式的解集为 .
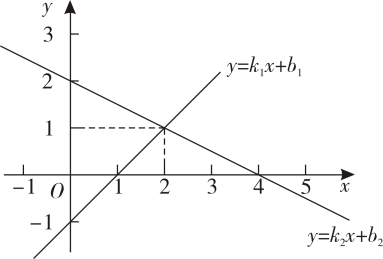 12. 如图,点A是反比例函数()图象上一点,轴于点且与反比例函数()的图象交于点B , , 连接 , , 若的面积为8,则 .
12. 如图,点A是反比例函数()图象上一点,轴于点且与反比例函数()的图象交于点B , , 连接 , , 若的面积为8,则 . 13. 如图,抛物线y=ax2+c与直线y=kx+m交于A(﹣3,y1)、B(1,y2)两点,则关于x的不等式ax2+c≥﹣kx+m的解集是 .
13. 如图,抛物线y=ax2+c与直线y=kx+m交于A(﹣3,y1)、B(1,y2)两点,则关于x的不等式ax2+c≥﹣kx+m的解集是 . 14. 如图,抛物线y=ax2+5ax+4与x轴交于C,D两点,与y轴交于点B,过点B作平行于x轴的直线,交抛物线于点A,连结AD,BC.若点A关于直线BD的对称点恰好落在线段DC上,则a=.
14. 如图,抛物线y=ax2+5ax+4与x轴交于C,D两点,与y轴交于点B,过点B作平行于x轴的直线,交抛物线于点A,连结AD,BC.若点A关于直线BD的对称点恰好落在线段DC上,则a=. 15. 在平面直角坐标系中,点 , 点P的“变换点”Q的坐标定义如下:当时, , 当时, , 线段按上述“变换点”组成新图形,直线与新图形恰好有两个公共点,则k的取值范围 .16. 如图,将一把矩形直尺和一块含角的三角板摆放在平面直角坐标系中,在轴上,点与点重合,点在上,三角板的直角边交于点 , 反比例函数的图象恰好经过点 , 若直尺的宽 , 三角板的斜边 , 则 .
15. 在平面直角坐标系中,点 , 点P的“变换点”Q的坐标定义如下:当时, , 当时, , 线段按上述“变换点”组成新图形,直线与新图形恰好有两个公共点,则k的取值范围 .16. 如图,将一把矩形直尺和一块含角的三角板摆放在平面直角坐标系中,在轴上,点与点重合,点在上,三角板的直角边交于点 , 反比例函数的图象恰好经过点 , 若直尺的宽 , 三角板的斜边 , 则 .
三、解答题
-
17. 如图,一次函数的图与反比例函数的图象交于A(﹣2,m),B(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D.
 (1)、求这两个函数的解析式;(2)、求△ADC的面积;(3)、根据图象直接写出不等式的解集.18. 小宇在学习过程中遇到了一个函数 .
(1)、求这两个函数的解析式;(2)、求△ADC的面积;(3)、根据图象直接写出不等式的解集.18. 小宇在学习过程中遇到了一个函数 .下面是小宇对其探究的过程,请补充完整:
 (1)、对于函数 , 当时,随的增大而减小,
(1)、对于函数 , 当时,随的增大而减小,对于函数 , 当时,随的增大
而结合上述分析,进一步探究发现,对于函数 , 当时,随的增大而;
(2)、当时,对于函数与的几组对应值如下表:在平面直角坐标系中,画出当时函数的图象.
(3)、过点作平行于轴的直线 , 结合的分析,解决问题:若直线与函数的图象有两个交点,则 .
19. 如图,已知直线l:y=x+4与反比例函数的图象交于点A(﹣1,n),直线l'经过点A , 且与l关于直线x=﹣1对称. (1)、求反比例函数的解析式;(2)、求图中阴影部分的面积;(3)、已知直线l:y=x+4与反比例函数的图象交于点另一点B , P在平面内,若以点A , B , P , O为顶点的四边形是平行四边形,请直接写出所有符合条件点P的坐标.20. 已知抛物线(是常数).(1)、求证:该抛物线的顶点在函数的图象上;(2)、若点在该抛物线上,且 , 求的取值范围.21. 如图所示,在平面直角坐标系中,抛物线y=ax2+bx+3经过点 A(-1,0),B(3,0),与 y轴交于点C,直线 y=x+2与y轴交于点D,交抛物线于E,F两点,点P为线段EF上一个动点(与E,F不重合),PQ∥y轴与抛物线交于点Q.
(1)、求反比例函数的解析式;(2)、求图中阴影部分的面积;(3)、已知直线l:y=x+4与反比例函数的图象交于点另一点B , P在平面内,若以点A , B , P , O为顶点的四边形是平行四边形,请直接写出所有符合条件点P的坐标.20. 已知抛物线(是常数).(1)、求证:该抛物线的顶点在函数的图象上;(2)、若点在该抛物线上,且 , 求的取值范围.21. 如图所示,在平面直角坐标系中,抛物线y=ax2+bx+3经过点 A(-1,0),B(3,0),与 y轴交于点C,直线 y=x+2与y轴交于点D,交抛物线于E,F两点,点P为线段EF上一个动点(与E,F不重合),PQ∥y轴与抛物线交于点Q. (1)、求抛物线的解析式.(2)、当P在什么位置时,四边形PDCQ为平行四边形?求出此时点P的坐标.
(1)、求抛物线的解析式.(2)、当P在什么位置时,四边形PDCQ为平行四边形?求出此时点P的坐标.四、综合题
-
22. 如图,一次函数与反比例函数的图象交于 , 两点.
 (1)、求一次函数的解析式;(2)、根据图象直接写出使成立的的取值范围;(3)、求得面积.23. 如图,反比例函数的图象与一次函数的图象交于第二象限的点、点 , 与轴交于点 , 其中点的坐标为 , 点的到轴的距离为 .
(1)、求一次函数的解析式;(2)、根据图象直接写出使成立的的取值范围;(3)、求得面积.23. 如图,反比例函数的图象与一次函数的图象交于第二象限的点、点 , 与轴交于点 , 其中点的坐标为 , 点的到轴的距离为 . (1)、试确定反比例函数的关系式;(2)、请用无刻度的直尺和圆规作出点关于直线的对称点(要求:不写作法,保留作图痕迹);(3)、点 , , 与(2)中的点 , 组成四边形 . 求证:四边形是菱形。24. 如图,正比例函数与反比例函数的图象交于、两点,的横坐标为 , 的纵坐标为 .
(1)、试确定反比例函数的关系式;(2)、请用无刻度的直尺和圆规作出点关于直线的对称点(要求:不写作法,保留作图痕迹);(3)、点 , , 与(2)中的点 , 组成四边形 . 求证:四边形是菱形。24. 如图,正比例函数与反比例函数的图象交于、两点,的横坐标为 , 的纵坐标为 .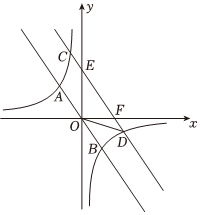 (1)、求反比例函数的表达式.(2)、观察图象,直接写出不等式的解集.(3)、将直线向上平移个单位,交双曲线于、两点,交坐标轴于点、 , 连接、 , 若的面积为 , 求直线的表达式.25. 在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数(k<0)的图象交于第二、四象限内的A , B两点,与x轴交于C点,过点A作AD⊥y轴,垂足为点D , OD=3, , 点B的坐标为(c , ﹣2).
(1)、求反比例函数的表达式.(2)、观察图象,直接写出不等式的解集.(3)、将直线向上平移个单位,交双曲线于、两点,交坐标轴于点、 , 连接、 , 若的面积为 , 求直线的表达式.25. 在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数(k<0)的图象交于第二、四象限内的A , B两点,与x轴交于C点,过点A作AD⊥y轴,垂足为点D , OD=3, , 点B的坐标为(c , ﹣2). (1)、求该反比例函数和一次函数的表达式;(2)、根据图象直接写出使ax+b<成立的x的取值范围;(3)、形如x2﹣a>0(a为常数,a>0)的解集为:x>或x<﹣ , 过点M(6,0)作垂直于x轴的直线MN , 直线y=x+n与双曲线y=(k<0)交于点P(x1 , y1),Q(x2 , y2),与直线MN交于点R(x3 , y3),若y1<y2<y3时,求n的取值范围.26. 如图①, , 反比例函数和()的图像分别是和 . 射线交于点 , 射线交于点 , 连接交y轴于点P , 轴.
(1)、求该反比例函数和一次函数的表达式;(2)、根据图象直接写出使ax+b<成立的x的取值范围;(3)、形如x2﹣a>0(a为常数,a>0)的解集为:x>或x<﹣ , 过点M(6,0)作垂直于x轴的直线MN , 直线y=x+n与双曲线y=(k<0)交于点P(x1 , y1),Q(x2 , y2),与直线MN交于点R(x3 , y3),若y1<y2<y3时,求n的取值范围.26. 如图①, , 反比例函数和()的图像分别是和 . 射线交于点 , 射线交于点 , 连接交y轴于点P , 轴.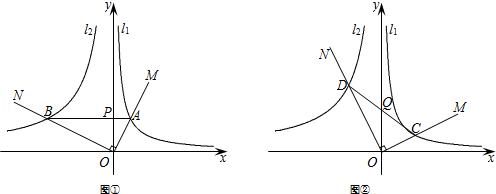 (1)、求的值;(2)、如图②,将绕点O旋转,射线始终在第一象限,交于点 , 射线交于点 , 连接交y轴于点 , 在旋转的过程中,的大小是否发生变化?若不变化,求出的值;若变化,请说明理由;(3)、在(2)的旋转过程中,当点为中点时,所在的直线与的有几个公共点,求出公共点的坐标.27. 如图,抛物线交轴于点 , 交轴于点 , 已知经过点 , 的直线的表达式为 .
(1)、求的值;(2)、如图②,将绕点O旋转,射线始终在第一象限,交于点 , 射线交于点 , 连接交y轴于点 , 在旋转的过程中,的大小是否发生变化?若不变化,求出的值;若变化,请说明理由;(3)、在(2)的旋转过程中,当点为中点时,所在的直线与的有几个公共点,求出公共点的坐标.27. 如图,抛物线交轴于点 , 交轴于点 , 已知经过点 , 的直线的表达式为 . (1)、求抛物线的函数表达式及其顶点的坐标;(2)、如图 , 点是线段上的一个动点,其中 , 作直线轴,交直线于 , 交抛物线于 , 作轴,交直线于点 , 四边形为矩形.设矩形的周长为 , 写出与的函数关系式,并求为何值时周长最大;
(1)、求抛物线的函数表达式及其顶点的坐标;(2)、如图 , 点是线段上的一个动点,其中 , 作直线轴,交直线于 , 交抛物线于 , 作轴,交直线于点 , 四边形为矩形.设矩形的周长为 , 写出与的函数关系式,并求为何值时周长最大;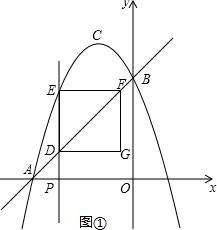 (3)、如图 , 在抛物线的对称轴上是否存在点 , 使点 , , 构成的三角形是以为腰的等腰三角形?若存在,直接写出所有符合条件的点的坐标;若不存在,请说明理由.28. 已知抛物线 , 其中是实数.(1)、已知三个点 , 其中有一个点是抛物线的顶点,请选出该点并求抛物线的解析式;(2)、在(1)的条件下,抛物线与轴交于两点(点在轴正半轴),与轴交于点 , 抛物线的顶点的记为 ,
(3)、如图 , 在抛物线的对称轴上是否存在点 , 使点 , , 构成的三角形是以为腰的等腰三角形?若存在,直接写出所有符合条件的点的坐标;若不存在,请说明理由.28. 已知抛物线 , 其中是实数.(1)、已知三个点 , 其中有一个点是抛物线的顶点,请选出该点并求抛物线的解析式;(2)、在(1)的条件下,抛物线与轴交于两点(点在轴正半轴),与轴交于点 , 抛物线的顶点的记为 ,①若点在点之间的抛物线上运动(不与点重合),连接交于点 , 连接 . 记的面积分别为 , 求的最大值;
②过点的直线与抛物线的另一个交点为 , 直线与直线交于点 , 过点作的垂线,交抛物线于点 , 过的中点作于点 . 求证: .
五、实践探究题
-
29. 阅读材料:
在平面直角坐标系xOy中,点P(x0,y0)到直线Ax+By+C=0的距离公式为: .
例如:求点P0(0,0)到直线4x+3y-3=0的距离.
解:由直线4x+3y-3=0知,A=4,B=3,C=-3,
∴点P0(0,0)到直线4x+3y-3=0的距离为
根据以上材料,解决下列问题:
(1)、问题1:点P1(3,4)到直线 的距离为;(2)、问题2:已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线 b相切,求实数b的值;(3)、问题3:如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出S△ABP的最大值和最小值. 30. 【探究函数 的图象与性质】(1)、函数 的自变量 的取值范围是;(2)、下列四个函数图象中函数 的图象大致是( );A、
30. 【探究函数 的图象与性质】(1)、函数 的自变量 的取值范围是;(2)、下列四个函数图象中函数 的图象大致是( );A、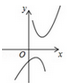 B、
B、 C、
C、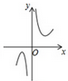 D、
D、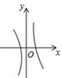 (3)、对于函数 ,求当 >0时, 的取值范围.
(3)、对于函数 ,求当 >0时, 的取值范围.请将下列的求解过程补充完整.
解:∵ >0
∴
∵
∴ ≥
(4)、【拓展运用】若函数 ,则 的取值范围.
31. 某班“数学兴趣小组”对函数的图象和性质进行了探究,探究过程如下,请补充完整.x
…
﹣3
﹣
﹣2
﹣1
0
1
2
3
…
y
…
﹣2
﹣
m
2
1
2
1
﹣
﹣2
…
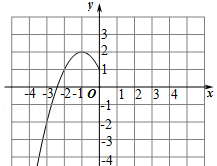 (1)、自变量x的取值范围是全体实数,x与y的几组对应值列表如上:其中m= .(2)、根据上表数据,在如图所示的平面直角坐标系中描点连线,画出了函数图象的一部分,请画出该函数图象的另一部分.(3)、观察函数图象,写出一条函数的性质.(4)、进一步探究函数图象发现:
(1)、自变量x的取值范围是全体实数,x与y的几组对应值列表如上:其中m= .(2)、根据上表数据,在如图所示的平面直角坐标系中描点连线,画出了函数图象的一部分,请画出该函数图象的另一部分.(3)、观察函数图象,写出一条函数的性质.(4)、进一步探究函数图象发现:①方程有个实数根;
②关于x的方程有4个实数根时,a的取值范围是 .